次短路与 k 短路
次短路
严格次短路
基本思路:两个 dis 数组分别储存最短路和次短路,依然使用堆优 Dij。
显然,堆优部分是不变的。
struct node{
int id,val;
bool operator <(const node &b)const
{
return val>b.val;
}
};
priority_queue<node>h;
而在遍历时,也就是多了个 if 判断和次短路的更新。
memset(dis1,127,sizeof(dis1));
memset(dis2,127,sizeof(dis2));
dis1[1]=0;h.push((node){1,0});
while(h.size())
{
node now=h.top();h.pop();
if(now.val>dis2[now.id])
continue;//不知道有没有用的瞎剪枝
for(int i=fir[now.id];i;i=nex[i])
{
int p=poi[i];
if(dis1[p]>now.val+val[i])
{
dis2[p]=dis1[p];//更新次短路
dis1[p]=now.val+val[i];//更新最短路
h.push((node){p,dis1[p]});
}
if(dis1[p]<now.val+val[i]&&now.val+val[i]<dis2[p])
{//更新次短路
dis2[p]=now.val+val[i];
h.push((node){p,dis2[p]});
}
}
}
而为什么又要将更新次短路的点加入到堆中呢?
举个例子:
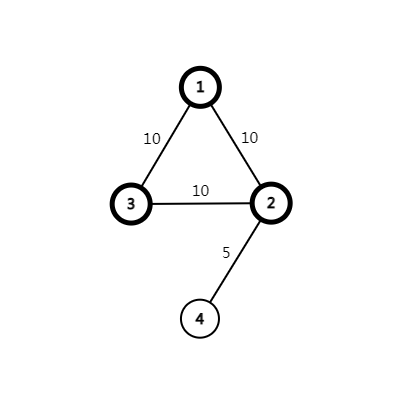
此时,\(dis1_2=10,dis2_2=20\),存在一条 \(2\) 到 \(4\) 的权值为 \(5\) 的边。
若 \(dis_2\) 不入堆,那么之后的操作中 \(dis1_4=15,dis2_4=+\infty\)。
只有当堆里有 \(dis2_2=20\),才能维护出 \(dis2_4=dis2_2+val_{2,4}=20+5=25\)。
非严格次短路
显然,对于已求得的最短路,删除非最短路上的边对最短路并无影响
但删除最短路上的边就会有一些影响。
所以可以先求出最短路径,然后尝试删掉最短路中的每一条边,并每次求出删边之后的最短路。
取最小者即为非严格次短路。
double dij(int u,int v)
{
priority_queue<node>h;
memset(dis,127,sizeof(dis));
memset(vis,0,sizeof(vis));
dis[1]=0;h.push((node){1,0});
while(h.size())
{
int now=h.top().to;h.pop();
if(vis[now])continue;
vis[now]=1;
for(int i=fir[now];i;i=nex[i])
{
int p=poi[i];
if((now==u&&p==v)||(now==v&&p==u))
continue;
if(dis[p]>dis[now]+val[i])
{
dis[p]=dis[now]+val[i];
h.push((node){p,dis[p]});
}
}
}
return dis[n];
}
memset(dis,127,sizeof(dis));
queue<int>h;h.push(1);
dis[1]=0,vis[1]=1;
while(h.size())
{
int now=h.front();h.pop();
vis[now]=0;
for(int i=fir[now];i;i=nex[i])
{
int p=poi[i];
if(dis[p]>dis[now]+val[i])
{
dis[p]=dis[now]+val[i];
pre[p]=now;
if(vis[p])continue;
h.push(p),vis[p]=1;
}
}
}
for(int i=n;i^1;i=pre[i])
ans=min(ans,dij(i,pre[i]));
k 短路
维护 k 短路,一种简单的方法是用 A* 进行启发式搜索。
A*,就是运用估价函数进行启发式搜索,就是对 bfs+priority_queue 的优化,其本质还是搜索。
关键就是估价函数的生成。
对于 k 短路问题而言,估价函数的生成就是在反图中跑一遍最短路。
一般来说,k 短路的题,数据范围都不是很大。
欢迎收看大型纪录片:《SPFA的复活之路》
struct edge{
int to,val;
};
vector<edge>e[inf];
int dis[inf];bool vis[inf];
queue<int>q;
void SPFA()
{
memset(dis,127,sizeof(dis));
dis[1]=0;q.push(1);
while(q.size())
{
int now=q.front();q.pop();
vis[now]=0;
int len=e[now].size();
for(int i=0;i<len;i++)
{
int p=e[now][i].to;
if(dis[p]>dis[now]+e[now][i].val)
{
dis[p]=dis[now]+e[now][i].val;
if(vis[now])continue;
q.push(p);vis[p]=1;
}
}
}
}
然后和 dijkstra 使用优先队列差不多,只不过需要多维护一个东西:起点到当前点的实际代价与当前点到终点的预估代价之和。
struct Astar{
int id,val,guj;
Astar(int id,int val,int guj):
id(id),val(val),guj(guj){}
bool operator <(const Astar &b)const
{
return guj>b.guj;
}
};
priority_queue<Astar>h;
显然,第一次走到终点为最短路,第二次为次短路,以此类推。
显然,找到 k 条路径之后,优先队列里剩下的点对答案均没有贡献,直接结束就可。
然后就可以暴搜了。
int fir[inf],nex[inf],poi[inf],val[inf],cnt;
void ins(int x,int y,int z)
{
nex[++cnt]=fir[x];
poi[cnt]=y;
val[cnt]=z;
fir[x]=cnt;
}
struct Astar{
int id,val,guj;
Astar(int id,int val,int guj):
id(id),val(val),guj(guj){}
bool operator <(const Astar &b)const
{
return guj>b.guj;
}
};
priority_queue<Astar>h;
void A_star()
{
h.push(Astar(n,0,dis[n]));
while(h.size())
{
Astar now=h.top();h.pop();
if(now.id==1)
{
wr(now.val,'\n');
if(--k==0)break;
}
for(int i=fir[now.id];i;i=nex[i])
{
int p=poi[i],to=now.val+val[i];
h.push(Astar(p,to,to+dis[p]));
}
}
while(k--)wr(-1,'\n');
}
属实暴力。
若找不到 k 条路径,剩下的均输出 -1。
AC Code:
int n,m,k;
struct edge{
int to,val;
};
vector<edge>e[inf];
int dis[inf];
bool vis[inf];
queue<int>q;
int fir[inf],nex[inf],poi[inf],val[inf],cnt;
void ins(int x,int y,int z)
{
nex[++cnt]=fir[x];
poi[cnt]=y;
val[cnt]=z;
fir[x]=cnt;
}
struct Astar{
int id,val,guj;
Astar(int id,int val,int guj):
id(id),val(val),guj(guj){}
bool operator <(const Astar &b)const
{
return guj>b.guj;
}
};
priority_queue<Astar>h;
int main()
{
n=re();m=re();k=re();
for(int i=1;i<=m;i++)
{
int u=re(),v=re(),w=re();
ins(u,v,w);
e[v].push_back((edge){u,w});
}
memset(dis,127,sizeof(dis));
dis[1]=0;q.push(1);
while(q.size())
{
int now=q.front();q.pop();
vis[now]=0;
int len=e[now].size();
for(int i=0;i<len;i++)
{
int p=e[now][i].to;
if(dis[p]>dis[now]+e[now][i].val)
{
dis[p]=dis[now]+e[now][i].val;
if(vis[now])continue;
q.push(p);vis[p]=1;
}
}
}
h.push(Astar(n,0,dis[n]));
while(h.size())
{
Astar now=h.top();h.pop();
if(now.id==1)
{
wr(now.val,'\n');
if(--k==0)break;
}
for(int i=fir[now.id];i;i=nex[i])
{
int p=poi[i],to=now.val+val[i];
h.push(Astar(p,to,to+dis[p]));
}
}
while(k--)wr(-1,'\n');
return 0;
}
时间复杂度分析
虽然是启发式搜索,但上界仍然是暴力的上界 \(O(nk\log n)\),但大多数情况下跑不满。
不过,用 A* 这种简单的算法骗到大部分分,它不香吗。
当然,A* 还可以用可持久化可并堆优化,详见 OI-wiki。


