Fhq_Treap 和 Splay：谁才是序列之王？

平衡树

很久以前，我立志要学习所有的平衡树，然后把每个树的学习笔记都整理到相关博客中。

而如今……

今年欢笑复明年，不知退役在眼前。

在阅读本文之前建议先学习二叉搜索树相关内容。

Fhq_Treap

原来 Treap 是一种旋转类的平衡树（即树堆），然后由~~防火墙~~范浩强神犇发明了一种不需要旋转的 Treap，凭借其短小的代码而不失精悍的功能（区间操作和可持久化）博得众人喜爱。

比起“普通平衡树”、“文艺平衡树”这种叫法，我更喜欢叫其“权值树”、“区间树”。

基本概念与储存

众所周知，BST 在极端数据（顺序插入单调值）时会退化成链，深度为 $O(n)$ ；而 heap 是一种完全二叉树，深度总是维持在 $O(\log n)$ 。

Treap 是将 BST 和 heap 结合在一起的数据结构（Treap=Tree+heap），使得整棵树的深度大致维护在 $O(\log n)$ 左右。

不过，根据 BST 和 heap 的性质，这两个数据结构好像是冲突的，那要如何结合在一起呢？

毕竟 heap 是辅助 BST 的工具，所以，对 BST 的每个节点赋一个值 pri，使得 val 满足 BST 性质，pri 满足 heap 性质。

也就是这样：

 struct Fhq_Treap{
	int lc,rc;
	int siz,val,pri;
}T[inf];

而这个 pri 值，随机就好。

不要不相信随机数，它可是很好用的！

可以理解为将原来的插入序列随机打乱，这样树的深度就维持在 $O(\log n)$ 级别了。

图示：

实现权值平衡树

了解了 Treap 的基本概念，接下来就是 Fhq_Treap 的两个 最最最重要 的操作：分裂（split）和合并（merge）。

为什么说最最最重要？因为这两个操作插入要用到，删除要用到，查询排名、k 小值、前驱后继都要用到。

分裂-split

分裂操作包含两类：按值分裂和按大小分裂。

第二种分裂方式会在下边的区间平衡树中提到。权值树中，用到的分裂方式为第一种。

split 函数包含四个参数：将原树 $i$ 按照 $k$ 分裂为 $x,y$ 两棵树，其中 $x$ 树中的 val 均 $\le k$ ， $y$ 树中的 val 均 $>k$ 。

由于 val 满足 BST 性质，每找到一个节点，若当前节点的 val $\le k$ ，那么其左子树的 val 均 $\le k$ ，就将当前节点和左子树从 $i$ 上拆下来，拼到 $x$ 树上去；否则，其右子树的 val 均 $>k$ ，将当前节点和右子树从 $i$ 上拆下来，拼到 $y$ 树上去。

图示：

函数实现：

 void split(int i,int k,int &x,int &y)
{
	if(!i){x=y=0;return;}
	if(T[i].val<=k)
		x=i,split(T[i].rc,k,T[i].rc,y);
	else y=i,split(T[i].lc,k,x,T[i].lc);
	pushup(i);
}

合并-merge

为了方便实现，我们保证 $x$ 的 val 均比 $y$ 的 val 小。

那么合并的时候也就只需要比较两个节点的 pri 了。

既然 val 确定了，合并之后的情况就只有两种：

区别就是选择大根堆还是小根堆。

通过比较，就可以确定是将 $x$ 的右子树与 $y$ 合并还是将 $x$ 与 $y$ 的左子树合并。

至于具体的比较方案，两种应该是都可以的，毕竟堆性质的维护不会影响 BST 的性质。

但就在某天（2022 年 10 月 1 日），发生了一个玄学错误，至今未得解，可以看看这个帖子。

图示（这个图有两处错误，但可以更了解基本思想）：

 int merge(int x,int y)
{
	if(!x||!y)return x|y;
	if(T[x].pri<T[y].pri)
	{
		T[x].rc=merge(T[x].rc,y);
		pushup(x);return x;
	}
	else
	{
		T[y].lc=merge(x,T[y].lc);
		pushup(y);return y;
	}
}

其他操作

接下来，你将明白，什么叫短小精悍！

1. `pushup`

上边两段代码中都有 pushup 操作。和 BST 相同，在权值树中，pushup 的功能就是统计以当前节点为根的子树大小。

 void pushup(int i)
{
	T[i].siz=T[T[i].lc].siz+T[T[i].rc].siz+1;
}

2. `new_ k`

新建一个 val 为 k 的节点。

 #include<random>
mt19937 rnd(51205);
int new_(int k)
{
	T[++cnt].pri=rnd();
	T[cnt].siz=1;T[cnt].val=k;
	return cnt;
}

mt19937 是一种神奇的随机数生成器，想深入了解的可以查阅这篇日报。

而 51205 是对我有重要意义的一个数字。

3. `insert k`

将原树按 $k$ 分裂，然后新建一个节点（看做一棵新的树），将三棵树合并即可。

 void insert(int k)
{
	split(rot,k,rx,ry);
	rot=merge(merge(rx,new_(k)),ry);
}

为了防止变量名冲突，我将原树树根记作 $rot$ ，所用到的临时分裂出的树的树根分别记作 $rx,ry,rz$ ，而且保证点权关系为 $rx<ry<rz$ 。

4. `remove k`

先将 $rot$ 按 $k$ 分裂成 $rx,rz$ 两树，然后将 $rx$ 按 $k-1$ 分裂为 $rx,ry$ 两树。这样下来， $ry$ 上的点的点权均为 $k$ （如果有的话）。如果将所有 $k$ 均删除，则直接合并 $rx,rz$ 即可，否则先将 $ry$ 的左右子树合并，然后再将 $rx,ry,rz$ 合并即可。

 void remove(int k)
{
	split(rot,k,rx,rz);
	split(rx,k-1,rx,ry);
	ry=merge(T[ry].lc,T[ry].rc);
	rot=merge(merge(rx,ry),rz);
}

5. `ask_kth`

这应该是唯一一个和旋转类平衡树一样的操作了。

但由于某些情况下不只要查询整棵树的 $k$ 小值，所以参数有两个。

 int kth(int i,int k)
{
	while(1)
	{
		if(k==T[T[i].lc].siz+1)return T[i].val;
		if(k<=T[T[i].lc].siz)i=T[i].lc;
		else k-=T[T[i].lc].siz+1,i=T[i].rc;
	}
}

6. `ask_rank k`

将 $rot$ 按 $k-1$ 分裂为 $rx,ry$ 两棵树，那么 $k$ 的排名就是 $rx$ 的 $siz+1$ 。

 void ask_rank(int k)
{
	split(rot,k-1,rx,ry);
	wr(T[rx].siz+1),putchar('\n');
	rot=merge(rx,ry);
}

7. `ask_pre/ask_nex k`

本质上这两个操作是一样的，此处归为一类。

前驱：先将 $rot$ 按照 $k-1$ 分裂为 $rx,ry$ 两棵树，然后 $rx$ 中的最大值即为 $k$ 的前驱。

后继：先将 $rot$ 按照 $k$ 分裂为 $rx,ry$ 两棵树，然后 $ry$ 中的最小值即为 $k$ 的后继。

 void ask_pre(int k)
{
	split(rot,k-1,rx,ry);
	wr(kth(rx,T[rx].siz)),putchar('\n');
	rot=merge(rx,ry);
}
void ask_nex(int k)
{
	split(rot,k,rx,ry);
	wr(kth(ry,1)),putchar('\n');
	rot=merge(rx,ry);
}

完整代码

 const int inf=1e5+7;
int n,op,k;
struct Fhq_Treap{
	int lc,rc;
	int val,siz;
	unsigned pri;
}T[inf];
int cnt,rot,rx,ry,rz;
#include<random>
mt19937 rnd(51205);
int new_(int k)
{
	T[++cnt].pri=rnd();
	T[cnt].siz=1,T[cnt].val=k;
	return cnt;
}
void pushup(int i)
{
	T[i].siz=T[T[i].lc].siz+T[T[i].rc].siz+1;
}
void split(int i,int k,int &x,int &y)
{
	if(!i){x=y=0;return;}
	if(T[i].val<=k)
		x=i,split(T[i].rc,k,T[i].rc,y);
	else y=i,split(T[i].lc,k,x,T[i].lc);
	pushup(i);
}
int merge(int x,int y)
{
	if(!x||!y)return x|y;
	if(T[x].pri<T[y].pri)
	{
		T[x].rc=merge(T[x].rc,y);
		pushup(x);return x;
	}
	else
	{
		T[y].lc=merge(x,T[y].lc);
		pushup(y);return y;
	}
}
int kth(int i,int k)
{
	while(1)
	{
		if(k==T[T[i].lc].siz+1)return T[i].val;
		if(k<=T[T[i].lc].siz)i=T[i].lc;
		else k-=T[T[i].lc].siz+1,i=T[i].rc;
	}
}
void insert(int k)
{
	split(rot,k,rx,ry);
	rot=merge(merge(rx,new_(k)),ry);
}
void remove(int k)
{
	split(rot,k,rx,rz);
	split(rx,k-1,rx,ry);
	ry=merge(T[ry].lc,T[ry].rc);
	rot=merge(merge(rx,ry),rz);
}
void ask_rank(int k)
{
	split(rot,k-1,rx,ry);
	wr(T[rx].siz+1),putchar('\n');
	rot=merge(rx,ry);
}
void ask_kth(int k)
{
	wr(kth(rot,k)),putchar('\n');
}
void ask_pre(int k)
{
	split(rot,k-1,rx,ry);
	wr(kth(rx,T[rx].siz)),putchar('\n');
	rot=merge(rx,ry);
}
void ask_nex(int k)
{
	split(rot,k,rx,ry);
	wr(kth(ry,1)),putchar('\n');
	rot=merge(rx,ry);
}
int main()
{
	n=re();
	for(int i=1;i<=n;i++)
	{
		op=re(),k=re();
		if(op==1)insert(k);
		if(op==2)remove(k);
		if(op==3)ask_rank(k);
		if(op==4)ask_kth(k);
		if(op==5)ask_pre(k);
		if(op==6)ask_nex(k);
	}
	return 0;
}

指针版实现

 int n;
struct Fhq_Treap{
	int siz,val;unsigned pri;
	Fhq_Treap *lc,*rc;
	Fhq_Treap(){}
	Fhq_Treap(int siz,int val,unsigned pri,Fhq_Treap* lc,Fhq_Treap* rc):
		siz(siz),val(val),pri(pri),lc(lc),rc(rc){}
}*rot,*nul,*rx,*ry,*rz;
#include<random>
mt19937 rnd(51205);
Fhq_Treap* new_(int k)
{
	return new Fhq_Treap(1,k,rnd(),nul,nul);
}
void pushup(Fhq_Treap* &i){i->siz=i->lc->siz+i->rc->siz+1;}
void split(Fhq_Treap* i,int k,Fhq_Treap* &x,Fhq_Treap* &y)
{
	if(i==nul){x=y=nul;return;}
	if(i->val<=k)
		x=i,split(i->rc,k,i->rc,y);
	else y=i,split(i->lc,k,x,i->lc);
	pushup(i);
}
Fhq_Treap* merge(Fhq_Treap* x,Fhq_Treap* y)
{
	if(x==nul)return y;
	if(y==nul)return x;
	if(x->pri<y->pri)
	{
		x->rc=merge(x->rc,y);
		pushup(x);return x;
	}
	else
	{
		y->lc=merge(x,y->lc);
		pushup(y);return y;
	}
}
int kth(Fhq_Treap* i,int k)
{
	Fhq_Treap* now=i;
	while(1)
	{
		if(k==now->lc->siz+1)return now->val;
		if(k<=now->lc->siz)now=now->lc;
		else k-=now->lc->siz+1,now=now->rc;
	}
}
int main()
{
	n=re();
	nul=new Fhq_Treap(0,0,0,0,0);
	rot=rx=ry=rz=nul;
	while(n--)
	{
		int op=re(),k=re();
		if(op==1)
		{
			split(rot,k,rx,ry);
			rot=merge(merge(rx,new_(k)),ry);
		}
		if(op==2)
		{
			split(rot,k,rx,rz);
			split(rx,k-1,rx,ry);
			ry=merge(ry->lc,ry->rc);
			rot=merge(merge(rx,ry),rz);
		}
		if(op==3)
		{
			split(rot,k-1,rx,ry);
			wr(rx->siz+1),putchar('\n');
			rot=merge(rx,ry);
		}
		if(op==4)wr(kth(rot,k)),putchar('\n');
		if(op==5)
		{
			split(rot,k-1,rx,ry);
			wr(kth(rx,rx->siz)),putchar('\n');
			rot=merge(rx,ry);
		}
		if(op==6)
		{
			split(rot,k,rx,ry);
			wr(kth(ry,1)),putchar('\n');
			rot=merge(rx,ry);
		}
	}
	return 0;
}

实现区间平衡树

一般来说，线段树是用来维护区间的，平衡树是用来维护权值的。

不过，既然有权值线段树，那么也绝对会有区间平衡树。

显然，权值线段树能实现的平衡树都能实现，但区间平衡树能实现的，线段树不一定都能实现。

建树

权值平衡树是按权值建的树，而区间平衡树则需要按下标建树。

其实，Fhq_Treap 的建树并不需要一个新的函数，直接将新加入的点和之前的树合并即可。

建树完之后，树的中序遍历为原数组。

 for(int i=1;i<=n;i++)
	rot=merge(rot,new_(i));

分裂-split

按大小分裂后， $rx$ 的大小为 $k$ ，剩下的点则在 $ry$ 中。

那么通过比较当前节点的左子树的 siz 就可以确定当前节点应该在树 $rx$ 还是在树 $ry$ 。

而且可以连带着左子树或者右子树一起确定。

代码（和按值分裂差不多）：

 void split(int i,int k,int &x,int &y)
{
	if(!i){x=y=0;return;}
	if(T[i].tag)pushdown(i);
	if(k<=T[T[i].lc].siz)y=i,split(T[i].lc,k,x,T[i].lc);
	else x=i,split(T[i].rc,k-T[T[i].lc].siz-1,T[i].rc,y);
	pushup(i);
}

其中的 tag 会在接下来讲解。

翻转-reverse

首先考虑一下区间翻转的弱化版：翻转整个数组。

~~统计奇偶性，判断正序还是倒序输出。~~

其实就是交换每个点的左右子树。

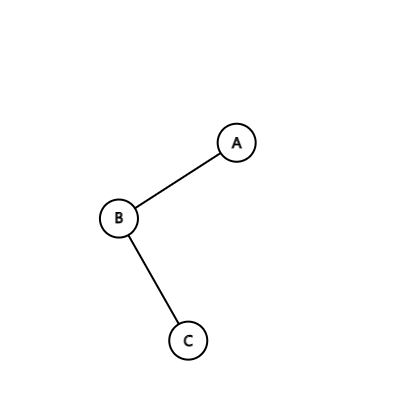
为什么这样是对的？

比如上图，按照中序遍历应该为 1 2 3，翻转之后应该是 3 2 1，也就是这个图：

感性理解一下，交换是对的。

那么怎么翻转一段区间呢？

翻转这段区间，首先要找到这段区间。

先将 $rot$ 按照 $r$ 分裂成 $rx,rz$ 两棵树，然后再将 $rx$ 按 $l-1$ 分裂成 $rx,ry$ 两棵树。

那么树 $ry$ 就代表区间 $l,r$ 。

这时，只需要翻转 $ry$ 就可以了。

单次操作最差时间复杂度为 $O(n)$ 。

总复杂度 $O(mn)$ 。

所以和暴力有什么区别？

码量更大？

当然不是。

稍微思考一下就可以发现，每次翻转不一定对之后的操作有影响。

看这句话是不是有点眼熟？

对，和线段树一样，加懒标。

用一个 tag 表示当前节点是否需要交换左右子节点，然后 pushdown 的时候交换左右子节点，然后下放懒标。

就像这样：

 void pushdown(int i)
{
	swap(T[i].lc,T[i].rc);
	T[T[i].lc].tag^=1;
	T[T[i].rc].tag^=1;
	T[i].tag=0;
}

至于何时下传，也和线段树一样，在穿过节点的时候下放，就像上边的 split，和下边的 merge。

 int merge(int x,int y)
{
	if(!x||!y)return x|y;
	if(T[x].pri<T[y].pri)
	{
		if(T[x].tag)pushdown(x);
		T[x].rc=merge(T[x].rc,y);
		pushup(x);return x;
	}
	else
	{
		if(T[y].tag)pushdown(y);
		T[y].lc=merge(x,T[y].lc);
		pushup(y);return y;
	}
}

AC Code

 const int inf=1e5+7;
int n,m;
struct Fhq_Treap{
	int lc,rc;
	int siz,val;
	unsigned pri;
	bool tag;
}T[inf];
int cnt,rot,rx,ry,rz;
#include<random>
mt19937 rnd(51205);
int new_(int k)
{
	T[++cnt].pri=rnd();
	T[cnt].siz=1;T[cnt].val=k;
	return cnt;
}
void pushup(int i)
{
	T[i].siz=T[T[i].lc].siz+T[T[i].rc].siz+1;
}
void pushdown(int i)
{
	swap(T[i].lc,T[i].rc);
	T[T[i].lc].tag^=1;
	T[T[i].rc].tag^=1;
	T[i].tag=0;
}
void split(int i,int k,int &x,int &y)
{
	if(!i){x=y=0;return;}
	if(T[i].tag)pushdown(i);
	if(k<=T[T[i].lc].siz)y=i,split(T[i].lc,k,x,T[i].lc);
	else x=i,split(T[i].rc,k-T[T[i].lc].siz-1,T[i].rc,y);
	pushup(i);
}
int merge(int x,int y)
{
	if(!x||!y)return x|y;
	if(T[x].pri<T[y].pri)
	{
		if(T[x].tag)pushdown(x);
		T[x].rc=merge(T[x].rc,y);
		pushup(x);return x;
	}
	else
	{
		if(T[y].tag)pushdown(y);
		T[y].lc=merge(x,T[y].lc);
		pushup(y);return y;
	}
}
void dfs(int i)
{
	if(T[i].tag)pushdown(i);
	if(T[i].lc)dfs(T[i].lc);
	wr(T[i].val),putchar(' ');
	if(T[i].rc)dfs(T[i].rc);
}
int main()
{
	n=re();m=re();
	for(int i=1;i<=n;i++)
		rot=merge(rot,new_(i));
	for(int i=1;i<=m;i++)
	{
		int l=re(),r=re();
		split(rot,r,rx,rz);
		split(rx,l-1,rx,ry);
		T[ry].tag^=1;
		rot=merge(merge(rx,ry),rz);
	}
	dfs(rot);
	return 0;
}

指针实现

 int n,m;
struct Fhq_Treap{
	int siz,val;
	unsigned pri;
	bool tag;
	Fhq_Treap *lc,*rc;
	Fhq_Treap(){}
	Fhq_Treap(int siz,int val,unsigned pri,bool tag,Fhq_Treap* lc,Fhq_Treap* rc):
		siz(siz),val(val),pri(pri),tag(tag),lc(lc),rc(rc){}
}*rot,*rx,*ry,*rz,*nul;
#include<random>
mt19937 rnd(51205);
Fhq_Treap* new_(int k)
{
	return new Fhq_Treap(1,k,rnd(),0,nul,nul);
}
void pushup(Fhq_Treap* &i)
{
	i->siz=i->lc->siz+i->rc->siz+1;
}
void pushdown(Fhq_Treap* i)
{
	swap(i->lc,i->rc);
	i->lc->tag^=1;
	i->rc->tag^=1;
	i->tag=0;
}
void split(Fhq_Treap* i,int k,Fhq_Treap* &x,Fhq_Treap* &y)
{
	if(i==nul){x=y=nul;return;}
	if(i->tag==1)pushdown(i);
	if(k<=i->lc->siz)y=i,split(i->lc,k,x,i->lc);
	else x=i,split(i->rc,k-i->lc->siz-1,i->rc,y);
	pushup(i);
}
Fhq_Treap* merge(Fhq_Treap* x,Fhq_Treap* y)
{
	if(x==nul)return y;
	if(y==nul)return x;
	if(x->pri<y->pri)
	{
		if(x->tag)pushdown(x);
		x->rc=merge(x->rc,y);
		pushup(x);return x;
	}
	else
	{
		if(y->tag)pushdown(y);
		y->lc=merge(x,y->lc);
		pushup(y);return y;
	}
}
void dfs(Fhq_Treap* i)
{
	if(i->tag)pushdown(i);
	if(i->lc!=nul)dfs(i->lc);
	wr(i->val),putchar(' ');
	if(i->rc!=nul)dfs(i->rc);
}
int main()
{
	n=re();m=re();
	nul=new Fhq_Treap(0,0,0,0,0,0);
	rot=rx=ry=rz=nul;
	for(int i=1;i<=n;i++)
		rot=merge(rot,new_(i));
	for(int i=1;i<=m;i++)
	{
		int l=re(),r=re();
		split(rot,r,rx,rz);
		split(rx,l-1,rx,ry);
		ry->tag^=1;
		rot=merge(merge(rx,ry),rz);
	}
	dfs(rot);
	return 0;
}

其他操作

当然，如果只能维护区间翻转，那区间平衡树的存在实在是太鸡肋了。

但是，区间平衡树的强大，远不止区间翻转。线段树支持的区间操作，区间平衡树都可以维护。

比如区间加、区间乘、区间推平、区间最值、区间求和、区间最大子段和等等等等。

就以大家最熟悉的线段树模板为例，用 Fhq_Treap 实现就是这样：

 int n,m,k;
struct Fhq_Treap{
	int siz,val,sum,tag;
	unsigned pri;
	Fhq_Treap *lc,*rc;
	Fhq_Treap(int siz,int val,int sum,int tag,unsigned pri,Fhq_Treap* lc,Fhq_Treap* rc):
		siz(siz),val(val),sum(sum),tag(tag),pri(pri),lc(lc),rc(rc){}
}*rot,*rx,*ry,*rz,*nul;
#include<random>
mt19937 rnd(51205);
Fhq_Treap* new_(int k)
{
	return new Fhq_Treap(1,k,k,0,rnd(),nul,nul);
}
void pushup(Fhq_Treap* &i)
{
	i->siz=i->lc->siz+i->rc->siz+1;
	i->sum=i->lc->sum+i->rc->sum+i->val;
}
void pushdown(Fhq_Treap* &i)
{
	i->lc->val+=i->tag;i->lc->tag+=i->tag;
	i->rc->val+=i->tag;i->rc->tag+=i->tag;
	i->lc->sum+=i->tag*i->lc->siz;
	i->rc->sum+=i->tag*i->rc->siz;
	i->tag=0;
}
void split(Fhq_Treap* i,int k,Fhq_Treap* &x,Fhq_Treap* &y)
{
	if(i==nul){x=y=nul;return;}
	if(i->tag)pushdown(i);
	if(k<=i->lc->siz)y=i,split(i->lc,k,x,i->lc);
	else x=i,split(i->rc,k-i->lc->siz-1,i->rc,y);
	pushup(i);
}
Fhq_Treap* merge(Fhq_Treap* x,Fhq_Treap* y)
{
	if(x==nul)return y;
	if(y==nul)return x;
	if(x->pri<y->pri)
	{
		if(x->tag)pushdown(x);
		x->rc=merge(x->rc,y);
		pushup(x);return x;
	}
	else
	{
		if(y->tag)pushdown(y);
		y->lc=merge(x,y->lc);
		pushup(y);return y;
	}
}
void update(int l,int r,int k)
{
	split(rot,r,rx,rz);
	split(rx,l-1,rx,ry);
	ry->val+=k,ry->tag+=k;
	ry->sum+=k*ry->siz;
	rot=merge(merge(rx,ry),rz);
}
int ask(int l,int r)
{
	split(rot,r,rx,rz);
	split(rx,l-1,rx,ry);
	int ret=ry->sum;
	rot=merge(merge(rx,ry),rz);
	return ret;
}
int main()
{
	n=re();m=re();
	nul=new Fhq_Treap(0,0,0,0,0,0,0);
	rot=rx=ry=rz=nul;
	for(int i=1;i<=n;i++)
		k=re(),rot=merge(rot,new_(k));
	while(m--)
	{
		int op=re(),l=re(),r=re();
		if(op==1)update(l,r,re());
		else wr(ask(l,r)),putchar('\n');
	}
	return 0;
}

虽然区间平衡树是按照下标建的树，但平衡树的节点上储存的还是权值。

这么看来，其实区间平衡树的基本思想就是将维护的区间单独拎出来，然后进行维护。

其实，Splay 区间维护的基本思想也是这样的。

区间平衡树好题：[NOI2005] 维护数列。

时间复杂度证明

Splay

基本概念与储存

Splay，又叫伸展树。

它的主要思想就是将通过伸展（splay）操作将使用频率较高的点旋转到距离根节点较近的位置。

至于怎么统计使用频率，其实并不需要很复杂，直接将每一次插入或查询的点 splay 到根即可。

由于某些操作需要知道一个节点的父节点是什么，所以要维护父指针。

并且为了旋转的方便，左右子节点用一个数组表示， $0$ 表示左儿子， $1$ 表示右儿子。

siz 表示子树大小，cnt 表示当前值出现了几次。

 struct Splay{
	int fa,hz[2];
	int siz,cnt,val;
}T[inf],q0;

树旋转

学习 Splay，首先需要掌握树旋转。

单旋

将某个节点旋转到根节点，首先需要知道这个节点的父节点是谁。

而且显然，旋转前后不能破坏 BST 的性质，也就是中序遍历单调这个性质不能变。

像这样：

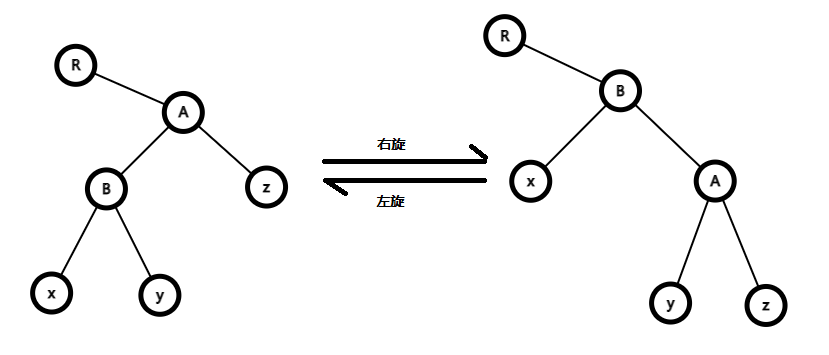
显然，中序遍历都是 RxByAz。

首先，我们要知道这个点是它的父节点的什么儿子：

 bool pd(int i)
{
	if(i==T[T[i].fa].hz[0])return 0;//左儿子
	else return 1;//右儿子
}

好像有点奇怪……

可以写成一行：

 bool pd(int i){return i==T[T[i].fa].hz[1];}

然后根据上图，我们要旋转 B。

B 是 A 的左儿子，所以旋转之后，A 就变成 B 的右儿子。

同时，B 的右儿子会变成 A 的左儿子。

而且，A 为 R 的右儿子，那么 B 将变为 R 的右儿子。

所以旋转操作共涉及到三组父子关系的建立。

代码实现是就是这样：

 void rotate(int i)
{
	int fa=T[i].fa,gf=T[fa].fa;
	int pdi=pd(i),pdf=pd(fa);
	T[i].fa=gf;if(gf)T[gf].hz[pdf]=i;
	T[fa].hz[pdi]=T[i].hz[pdi^1];
	if(T[i].hz[pdi^1])T[T[i].hz[pdi^1]].fa=fa;
	T[i].hz[pdi^1]=fa;T[fa].fa=i;
	pushup(fa),pushup(i);
}

在这里，我们用 i 表示当前节点，fa 表示当前节点的父亲节点，gf 表示当前节点的祖父节点。

由于 i 的子节点和祖父节点可能不存在（为 $0$ ），而在查询时可能会用到 $0$ 节点，所以建立关系时需要特判一下是否为 $0$ 。

pushup 和 Fhq_Treap 差不多，只不过 Splay 将相同权值储存在同一个点，需要 +cnt 而不是 +1。

 void pushup(int i)
{
	T[i].siz=T[T[i].hz[0]].siz+T[T[i].hz[1]].siz+T[i].cnt;
}

但是只有单旋的话，复杂度是错的，因此需要引入双旋。

伸展（双旋）

~~只有单旋的话，你写的不是 Splay，而是 Spaly~~

17 年安徽湖南省选也在抨击这种行为：https://www.luogu.com.cn/problem/P3721。

不过好像大多数题都没有刻意卡单旋，毕竟大多数出题人都默认大家都写双旋。

比如洛谷模板，比双旋跑得还快。

加强版倒是卡了一个点。

但如果考场上为了省这几行代码被卡，那就得不偿失了。

像 18 年 NOI 的归程，就卡了 SPFA……

splay(i,to)，就是将节点 i 伸展到 to 位置。

spaly 是这样写：

 void spaly(int i,int to)
{
	to=T[to].fa;
	while(T[i].fa^to)rotate(i);
	if(!to)rot=i;
}

很好理解，此处不再赘述。

因为我们的重点是复杂度正确的 Splay。

除去上述的两个单旋，Splay 还有四种旋转方式：

/ \ < >

看不懂？画个图：

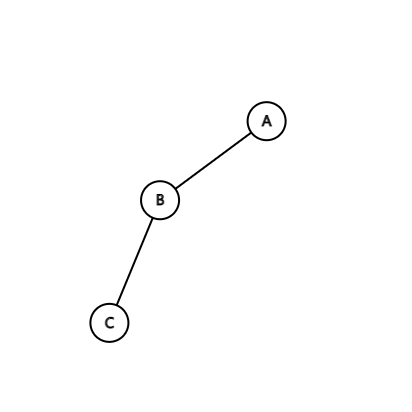
~~有没有感觉上边的符号很生动形象。~~

对于前两种情况，称为“一字型”，需要先旋 fa，再旋 i；而后两种情况称为“之字形”，则需旋两次 i。

不过，还有一种情况，就是只需要一步单旋就可以旋到 to。那么直接 rotate 即可。

写成代码就是这样：

 void splay(int i,int to)
{
	to=T[to].fa;
	int fa=T[i].fa;
	while(fa!=to)
	{
		if(T[fa].fa==to){rotate(i);break;}//最后一步单旋
		if(pd(i)^pd(fa))rotate(i);//之字形
		else rotate(fa);//一字型
		rotate(i);fa=T[i].fa;//最后一步都是旋 i
	}
	if(!to)rot=i;
}

不过，这个代码可以用三目运算符简化：

 void splay(int i,int to)
{
	to=T[to].fa;
	for(int fa=T[i].fa;fa!=to;rotate(i),fa=T[i].fa)
		if(T[fa].fa^to)rotate((pd(i)^pd(fa))?i:fa);
	if(!to)rot=i;
}

至此，树旋转完结撒花~~

实现权值平衡树

掌握了树旋转，也就掌握了 Splay。

插入-insert

按照 BST 的性质，找到 k 所对应的节点。然后 cnt++,siz++。

若找不到，则新建一个节点。

 int new_(int k,int fa)
{
	T[++cnt].fa=fa,T[cnt].val=k;
	T[cnt].siz=T[cnt].cnt=1;
	return cnt;
}

当然，都需要将节点 splay 到根。

 void insert(int k)
{
	if(!rot){rot=new_(k,0);return;}
	int now=rot,fa=0;
	while(now)
	{
		if(k==T[now].val)
		{
			T[now].siz++,T[now].cnt++;
			splay(now,rot);return;
		}
		fa=now;
		if(k<T[now].val)now=T[now].hz[0];
		else now=T[now].hz[1];
	}
	now=new_(k,fa);
	T[fa].hz[k>T[fa].val]=now;
	splay(now,rot);
}

排名-rank

与 BST 相同，左边多则查询左边，否则查询右边，顺便统计答案。

找不到则返回当前查询到的比 k 小的个数 +1。

 int ask_rnk(int k)
{
	int now=rot,ans=0;
	while(now)
	{
		if(k==T[now].val)
		{
			int ret=T[T[now].hz[0]].siz;
			splay(now,rot);
			return ans+ret+1;
		}
		if(k<T[now].val)now=T[now].hz[0];
		else ans+=T[T[now].hz[0]].siz+T[now].cnt,now=T[now].hz[1];
	}
	return ans+1;
}

k 小值-kth

和 Fhq_Treap 类似，但当前节点不一定只有一个 k，所以需要全部考虑。

 int ask_kth(int k)
{
	int now=rot;
	while(1)
	{
		if(T[T[now].hz[0]].siz+1<=k&&k<=T[T[now].hz[0]].siz+T[now].cnt)
			{splay(now,rot);return T[now].val;}
		if(k<=T[T[now].hz[0]].siz)now=T[now].hz[0];
		else k-=T[T[now].hz[0]].siz+T[now].cnt,now=T[now].hz[1];
	}
}

前驱、后继-pre/nex

前驱后继有些繁琐：

先将 k 插入并 splay 到根节点，此时 k 的前驱为左子树的最大值，后继为右子树的最小值。

找到之后，再将 k 删除即可。

 int pre()
{
	int now=T[rot].hz[0];
	if(now)
	{
		while(T[now].hz[1])
			now=T[now].hz[1];
		splay(now,rot);
	}
	return now;
}
int ask_pre(int k)
{
	insert(k);int ret=T[pre()].val;
	remove(k);return ret;
}
int nex()
{
	int now=T[rot].hz[1];
	if(now)
	{
		while(T[now].hz[0])
			now=T[now].hz[0];
		splay(now,rot);
	}
	return now;
}
int ask_nex(int k)
{
	insert(k);int ret=T[nex()].val;
	remove(k);return ret;
}

删除-remove

删除操作更为繁琐……

首先，用一个 ask_rnk 将 k 所在节点 splay 到根。

如果当前节点 cnt>1，则直接 cnt-- 即可。

如果当前节点没有子节点，直接将节点清空。

如果当前节点没有左儿子，就用右儿子取代当前节点。

同理，没有右儿子，就用做儿子取代当前节点。

否则，找到当前节点的前驱节点，并 Splay 到根。

此时待删除节点没有左儿子，用其右儿子取代待删除节点即可。

 void remove(int k)
{
	ask_rnk(k);int now=rot;
	if(T[now].cnt>1){T[now].cnt--,T[now].siz--;return;}
	if(T[now].hz[0]+T[now].hz[1]==0){clear(now),rot=0;return;}
	if(T[now].hz[0]==0)
	{
		rot=T[now].hz[1];T[rot].fa=0;
		pushup(rot);return;
	}
	if(T[now].hz[1]==0)
	{
		rot=T[now].hz[0];T[rot].fa=0;
		pushup(rot);return;
	}
	int ls=pre();
	splay(ls,rot);
	T[rot].hz[1]=T[now].hz[1];
	T[T[now].hz[1]].fa=rot;
	clear(now);pushup(rot);
}

其中的 clear 函数更为简单粗暴。由于使用的是结构体，可以直接赋值清零。

 void clear(int i){T[i]=q0;}

AC Code

 const int inf=1e5+7;
int n;
struct Splay{
	int fa,hz[2];
	int siz,cnt,val;
}T[inf],q0;
int rot,cnt;
void clear(int i){T[i]=q0;}
void pushup(int i){T[i].siz=T[T[i].hz[0]].siz+T[T[i].hz[1]].siz+T[i].cnt;}
bool pd(int i){return i==T[T[i].fa].hz[1];}
void rotate(int i)
{
	int fa=T[i].fa,gf=T[fa].fa;
	int pdi=pd(i),pdf=pd(fa);
	T[i].fa=gf;if(gf)T[gf].hz[pdf]=i;
	T[fa].hz[pdi]=T[i].hz[pdi^1];
	if(T[i].hz[pdi^1])T[T[i].hz[pdi^1]].fa=fa;
	T[i].hz[pdi^1]=fa;T[fa].fa=i;
	pushup(fa),pushup(i);
}
void splay(int now,int to)
{
	to=T[to].fa;
	for(int fa=T[now].fa;fa!=to;rotate(now),fa=T[now].fa)
		if(T[fa].fa^to)rotate((pd(now)^pd(fa))?now:fa);
	if(!to)rot=now;
}
int new_(int k,int fa)
{
	T[++cnt].fa=fa,T[cnt].val=k;
	T[cnt].siz=T[cnt].cnt=1;
	return cnt;
}
void insert(int k)
{
	if(!rot){rot=new_(k,0);return;}
	int now=rot,fa=0;
	while(now)
	{
		if(k==T[now].val)
		{
			T[now].siz++,T[now].cnt++;
			splay(now,rot);return;
		}
		fa=now;
		if(k<T[now].val)now=T[now].hz[0];
		else now=T[now].hz[1];
	}
	now=new_(k,fa);
	T[fa].hz[k>T[fa].val]=now;
	splay(now,rot);
}
int ask_rnk(int k)
{
	int now=rot,ans=0;
	while(now)
	{
		if(k==T[now].val)
		{
			int ret=T[T[now].hz[0]].siz;
			splay(now,rot);
			return ans+ret+1;
		}
		if(k<T[now].val)now=T[now].hz[0];
		else ans+=T[T[now].hz[0]].siz+T[now].cnt,now=T[now].hz[1];
	}
	return ans+1;
}
int ask_kth(int k)
{
	int now=rot;
	while(1)
	{
		if(T[T[now].hz[0]].siz+1<=k&&k<=T[T[now].hz[0]].siz+T[now].cnt)
			{splay(now,rot);return T[now].val;}
		if(k<=T[T[now].hz[0]].siz)now=T[now].hz[0];
		else k-=T[T[now].hz[0]].siz+T[now].cnt,now=T[now].hz[1];
	}
}
int pre()
{
	int now=T[rot].hz[0];
	if(now)
	{
		while(T[now].hz[1])
			now=T[now].hz[1];
		splay(now,rot);
	}
	return now;
}
int nex()
{
	int now=T[rot].hz[1];
	if(now)
	{
		while(T[now].hz[0])
			now=T[now].hz[0];
		splay(now,rot);
	}
	return now;
}
void remove(int k)
{
	ask_rnk(k);int now=rot;
	if(T[now].cnt>1){T[now].cnt--,T[now].siz--;return;}
	if(T[now].hz[0]+T[now].hz[1]==0){clear(now),rot=0;return;}
	if(T[now].hz[0]==0)
	{
		rot=T[now].hz[1];T[rot].fa=0;
		pushup(rot);return;
	}
	if(T[now].hz[1]==0)
	{
		rot=T[now].hz[0];T[rot].fa=0;
		pushup(rot);return;
	}
	int ls=pre();
	splay(ls,rot);
	T[rot].hz[1]=T[now].hz[1];
	T[T[now].hz[1]].fa=rot;
	clear(now);pushup(rot);
}
int ask_pre(int k)
{
	insert(k);int ret=T[pre()].val;
	remove(k);return ret;
}
int ask_nex(int k)
{
	insert(k);int ret=T[nex()].val;
	remove(k);return ret;
}
int main()
{
	n=re();
	for(int i=1;i<=n;i++)
	{
		int op=re(),k=re();
		if(op==1)insert(k);
		if(op==2)remove(k);
		if(op==3)wr(ask_rnk(k)),putchar('\n');
		if(op==4)wr(ask_kth(k)),putchar('\n');
		if(op==5)wr(ask_pre(k)),putchar('\n');
		if(op==6)wr(ask_nex(k)),putchar('\n');
	}
	return 0;
}

很抱歉，此代码没有指针版。

实现区间平衡树

在讲 Fhq_Treap 的提到过，两者实现区间操作的方式都是将区间单独拎出来。

Fhq_Treap 可以分裂，那么 Splay 怎么拎出来一个区间呢？

比如我们要操作的区间是 $[l,r]$ ，那么可以这样：

先将 $l-1$ 所对应的点伸展到根，再将 $r+1$ 所对应的点伸展到根的子节点。

这样， $r+1$ 节点的左儿子都比 $l-1$ 大，比 $r+1$ 小。也就是区间 $[l,r]$ 。

很容易发现，这里的 splay 和权值平衡树的 splay 不太一样。

权值平衡树那里是伸展到某个节点，而此处则有个操作是伸展到某个节点的子节点。

其实也很好维护，只需要将上述 splay 稍微改一下就好了：

 void splay(int i,int to)
{
	for(int fa=T[i].fa;fa!=to;rotate(i),fa=T[i].fa)
		if(T[fa].fa^to)rotate((pd(i)^pd(fa))?i:fa);
	if(!to)rot=i;
}

其实就少了一句话……

可能就有人会问了：那 splay 到根的操作怎么办？

显然，根的父节点为 $0$ ，所以 splay 到 $0$ 就好了。

至于怎么找节点，用类似于区间 k 小值的方式就好了。

拎出来之后，就可以进行区间操作了。

不过，如果想要翻转区间 $[1,n]$ ，则需要用到 $0$ 和 $n+1$ 。因此，在平衡树两端加上两个哨兵，以便于全局翻转。

AC Code

 const int inf=1e5+7;
int n,m,a[inf];
struct Splay{
	int fa,hz[2];
	int siz,val,tag;
}T[inf];
int rot,cnt;
void pushup(int i){T[i].siz=T[T[i].hz[0]].siz+T[T[i].hz[1]].siz+1;}
bool pd(int i){return T[T[i].fa].hz[1]==i;}
void build(int &i,int l,int r,int fa)
{
	if(l>r)return;
	int mid=(l+r)>>1;i=++cnt;
	T[i].val=a[mid];
	T[i].fa=fa;T[i].siz=1;
	build(T[i].hz[0],l,mid-1,i);
	build(T[i].hz[1],mid+1,r,i);
	pushup(i);
}
void rotate(int i)
{
	int fa=T[i].fa,gf=T[fa].fa;
	int pdi=pd(i),pdf=pd(fa);
	T[i].fa=gf;if(gf)T[gf].hz[pdf]=i;
	if(T[i].hz[pdi^1])T[T[i].hz[pdi^1]].fa=fa;
	T[fa].hz[pdi]=T[i].hz[pdi^1];
	T[fa].fa=i;T[i].hz[pdi^1]=fa;
	pushup(fa),pushup(i);
}
void splay(int i,int to)
{
	for(int fa=T[i].fa;fa!=to;rotate(i),fa=T[i].fa)
		if(T[fa].fa^to)rotate((pd(i)^pd(fa))?i:fa);
	if(!to)rot=i;
}
void pushdown(int i)
{
	T[T[i].hz[0]].tag^=1;
	T[T[i].hz[1]].tag^=1;
	swap(T[i].hz[0],T[i].hz[1]);
	T[i].tag=0;
}
int ask_kth(int k)
{
	int i=rot;
	while(1)
	{
		if(T[i].tag)pushdown(i);
		if(k==T[T[i].hz[0]].siz+1)return i;
		if(k<=T[T[i].hz[0]].siz)i=T[i].hz[0];
		else k-=T[T[i].hz[0]].siz+1,i=T[i].hz[1];
	}
}
void reverse(int l,int r)
{
	l=ask_kth(l),r=ask_kth(r);
	splay(l,0);splay(r,l);
	int pos=T[rot].hz[1];
	pos=T[pos].hz[0];
	T[pos].tag^=1;
}
void dfs(int now)
{
	if(!now)return;
	if(T[now].tag)pushdown(now);
	dfs(T[now].hz[0]);
	if((T[now].val^-1)&(T[now].val^inf))
		wr(T[now].val),putchar(' ');
	dfs(T[now].hz[1]);
}
int main()
{
	n=re();m=re();
	a[1]=-1,a[n+2]=inf;
	for(int i=1;i<=n;i++)a[i+1]=i;
	build(rot,1,n+2,0);
	for(int i=1;i<=m;i++)
	{
		int l=re()+1,r=re()+1;
		reverse(l-1,r+1);
	}
	dfs(rot);
	return 0;
}

同样，这份代码没有指针版。

其他操作

还是这个熟悉的线段树模板。

 const int inf=1e5+7;
int n,m,a[inf];
struct Splay{
	int fa,hz[2];
	int siz,val,sum,tag;
}T[inf];
int rot,cnt;
bool pd(int i){return T[T[i].fa].hz[1]==i;}
void pushup(int i)
{
	T[i].siz=T[T[i].hz[0]].siz+T[T[i].hz[1]].siz+1;
	T[i].sum=T[T[i].hz[0]].sum+T[T[i].hz[1]].sum+T[i].val;
}
void rotate(int i)
{
	int fa=T[i].fa,gf=T[fa].fa;
	bool pdi=pd(i),pdf=pd(fa);
	T[i].fa=gf;if(gf)T[gf].hz[pdf]=i;
	if(T[i].hz[pdi^1])T[T[i].hz[pdi^1]].fa=fa;
	T[fa].hz[pdi]=T[i].hz[pdi^1];
	T[fa].fa=i;T[i].hz[pdi^1]=fa;
	pushup(fa),pushup(fa);
}
void splay(int i,int to)
{
	for(int fa=T[i].fa;fa!=to;rotate(i),fa=T[i].fa)
		if(T[fa].fa^to)rotate((pd(i)^pd(fa))?i:fa);
	if(!to)rot=i;
}
void build(int &i,int l,int r,int fa)
{
	if(l>r)return;
	int mid=(l+r)>>1;i=++cnt;
	T[i].val=a[mid];
	T[i].siz=1,T[i].fa=fa;
	build(T[i].hz[0],l,mid-1,i);
	build(T[i].hz[1],mid+1,r,i);
	pushup(i);
}
void pushdown(int i)
{
	T[T[i].hz[0]].sum+=T[T[i].hz[0]].siz*T[i].tag;
	T[T[i].hz[1]].sum+=T[T[i].hz[1]].siz*T[i].tag;
	T[T[i].hz[0]].val+=T[i].tag;T[T[i].hz[1]].val+=T[i].tag;
	T[T[i].hz[0]].tag+=T[i].tag;T[T[i].hz[1]].tag+=T[i].tag;
	T[i].tag=0;
}
int kth(int k)
{
	int i=rot;
	while(1)
	{
		pushdown(i);
		if(k==T[T[i].hz[0]].siz+1)return i;
		if(k<=T[T[i].hz[0]].siz)i=T[i].hz[0];
		else k-=T[T[i].hz[0]].siz+1,i=T[i].hz[1];
	}
}
void update(int l,int r,int k)
{
	l=kth(l-1),r=kth(r+1);
	splay(l,0),splay(r,l);
	int pos=T[T[rot].hz[1]].hz[0];
	T[pos].sum+=T[pos].siz*k;
	T[pos].val+=k;T[pos].tag+=k;
}
int ask(int l,int r)
{
	l=kth(l-1),r=kth(r+1);
	splay(l,0),splay(r,l);
	int pos=T[T[rot].hz[1]].hz[0];
	return T[pos].sum;
}
signed main()
{
	n=re();m=re();
	for(int i=1;i<=n;i++)
		a[i+1]=re();
	build(rot,1,n+2,0);
	while(m--)
	{
		int op=re(),l=re()+1,r=re()+1;
		if(op==1)update(l,r,re());
		else wr(ask(l,r)),putchar('\n');
	}
	return 0;
}

时间复杂度证明

可持久化

~~不会。~~

posted @ 2022-10-02 10:44 Zvelig1205 阅读(2056) 评论(0) 编辑收藏举报

刷新页面返回顶部

登录后才能查看或发表评论，立即登录或者逛逛博客园首页

相关博文：

· BST 与 Treap

· 大树套小树

· 平衡树——fhq_treap

· 「学习笔记」平衡树基础：Splay 和 Treap

· FHQ-treap 学习笔记

阅读排行：
· winform 绘制太阳，地球，月球运作规律
· TypeScript + Deepseek 打造卜卦网站：技术与玄学的结合
· AI 智能体引爆开源社区「GitHub 热点速览」
· Manus的开源复刻OpenManus初探
· 写一个简单的SQL生成工具

公告

昵称： Zvelig1205
园龄： 3年7个月
粉丝： 17
关注： 2

+加关注

2025年3月

日

一

二

三

四

五

六

随笔分类

随笔档案

阅读排行榜

评论排行榜

1. 分块九讲(1)

	void split(int i,int k,int &x,int &y)
	{
	if(!i){x=y=0;return;}
	if(T[i].val<=k)
	x=i,split(T[i].rc,k,T[i].rc,y);
	else y=i,split(T[i].lc,k,x,T[i].lc);
	pushup(i);
	}

	int merge(int x,int y)
	{
	if(!x\|\|!y)return x\|y;
	if(T[x].pri<T[y].pri)
	{
	T[x].rc=merge(T[x].rc,y);
	pushup(x);return x;
	}
	else
	{
	T[y].lc=merge(x,T[y].lc);
	pushup(y);return y;
	}
	}

	void pushup(int i)
	{
	T[i].siz=T[T[i].lc].siz+T[T[i].rc].siz+1;
	}

	#include<random>
	mt19937 rnd(51205);
	int new_(int k)
	{
	T[++cnt].pri=rnd();
	T[cnt].siz=1;T[cnt].val=k;
	return cnt;
	}

	void insert(int k)
	{
	split(rot,k,rx,ry);
	rot=merge(merge(rx,new_(k)),ry);
	}

	void remove(int k)
	{
	split(rot,k,rx,rz);
	split(rx,k-1,rx,ry);
	ry=merge(T[ry].lc,T[ry].rc);
	rot=merge(merge(rx,ry),rz);
	}

	int kth(int i,int k)
	{
	while(1)
	{
	if(k==T[T[i].lc].siz+1)return T[i].val;
	if(k<=T[T[i].lc].siz)i=T[i].lc;
	else k-=T[T[i].lc].siz+1,i=T[i].rc;
	}
	}

	void ask_rank(int k)
	{
	split(rot,k-1,rx,ry);
	wr(T[rx].siz+1),putchar('\n');
	rot=merge(rx,ry);
	}

	void ask_pre(int k)
	{
	split(rot,k-1,rx,ry);
	wr(kth(rx,T[rx].siz)),putchar('\n');
	rot=merge(rx,ry);
	}
	void ask_nex(int k)
	{
	split(rot,k,rx,ry);
	wr(kth(ry,1)),putchar('\n');
	rot=merge(rx,ry);
	}

	const int inf=1e5+7;
	int n,op,k;
	struct Fhq_Treap{
	int lc,rc;
	int val,siz;
	unsigned pri;
	}T[inf];
	int cnt,rot,rx,ry,rz;
	#include<random>
	mt19937 rnd(51205);
	int new_(int k)
	{
	T[++cnt].pri=rnd();
	T[cnt].siz=1,T[cnt].val=k;
	return cnt;
	}
	void pushup(int i)
	{
	T[i].siz=T[T[i].lc].siz+T[T[i].rc].siz+1;
	}
	void split(int i,int k,int &x,int &y)
	{
	if(!i){x=y=0;return;}
	if(T[i].val<=k)
	x=i,split(T[i].rc,k,T[i].rc,y);
	else y=i,split(T[i].lc,k,x,T[i].lc);
	pushup(i);
	}
	int merge(int x,int y)
	{
	if(!x\|\|!y)return x\|y;
	if(T[x].pri<T[y].pri)
	{
	T[x].rc=merge(T[x].rc,y);
	pushup(x);return x;
	}
	else
	{
	T[y].lc=merge(x,T[y].lc);
	pushup(y);return y;
	}
	}
	int kth(int i,int k)
	{
	while(1)
	{
	if(k==T[T[i].lc].siz+1)return T[i].val;
	if(k<=T[T[i].lc].siz)i=T[i].lc;
	else k-=T[T[i].lc].siz+1,i=T[i].rc;
	}
	}
	void insert(int k)
	{
	split(rot,k,rx,ry);
	rot=merge(merge(rx,new_(k)),ry);
	}
	void remove(int k)
	{
	split(rot,k,rx,rz);
	split(rx,k-1,rx,ry);
	ry=merge(T[ry].lc,T[ry].rc);
	rot=merge(merge(rx,ry),rz);
	}
	void ask_rank(int k)
	{
	split(rot,k-1,rx,ry);
	wr(T[rx].siz+1),putchar('\n');
	rot=merge(rx,ry);
	}
	void ask_kth(int k)
	{
	wr(kth(rot,k)),putchar('\n');
	}
	void ask_pre(int k)
	{
	split(rot,k-1,rx,ry);
	wr(kth(rx,T[rx].siz)),putchar('\n');
	rot=merge(rx,ry);
	}
	void ask_nex(int k)
	{
	split(rot,k,rx,ry);
	wr(kth(ry,1)),putchar('\n');
	rot=merge(rx,ry);
	}
	int main()
	{
	n=re();
	for(int i=1;i<=n;i++)
	{
	op=re(),k=re();
	if(op==1)insert(k);
	if(op==2)remove(k);
	if(op==3)ask_rank(k);
	if(op==4)ask_kth(k);
	if(op==5)ask_pre(k);
	if(op==6)ask_nex(k);
	}
	return 0;
	}

	int n;
	struct Fhq_Treap{
	int siz,val;unsigned pri;
	Fhq_Treap lc,rc;
	Fhq_Treap(){}
	Fhq_Treap(int siz,int val,unsigned pri,Fhq_Treap* lc,Fhq_Treap* rc):
	siz(siz),val(val),pri(pri),lc(lc),rc(rc){}
	}rot,nul,rx,ry,*rz;
	#include<random>
	mt19937 rnd(51205);
	Fhq_Treap* new_(int k)
	{
	return new Fhq_Treap(1,k,rnd(),nul,nul);
	}
	void pushup(Fhq_Treap* &i){i->siz=i->lc->siz+i->rc->siz+1;}
	void split(Fhq_Treap* i,int k,Fhq_Treap* &x,Fhq_Treap* &y)
	{
	if(i==nul){x=y=nul;return;}
	if(i->val<=k)
	x=i,split(i->rc,k,i->rc,y);
	else y=i,split(i->lc,k,x,i->lc);
	pushup(i);
	}
	Fhq_Treap* merge(Fhq_Treap* x,Fhq_Treap* y)
	{
	if(x==nul)return y;
	if(y==nul)return x;
	if(x->pri<y->pri)
	{
	x->rc=merge(x->rc,y);
	pushup(x);return x;
	}
	else
	{
	y->lc=merge(x,y->lc);
	pushup(y);return y;
	}
	}
	int kth(Fhq_Treap* i,int k)
	{
	Fhq_Treap* now=i;
	while(1)
	{
	if(k==now->lc->siz+1)return now->val;
	if(k<=now->lc->siz)now=now->lc;
	else k-=now->lc->siz+1,now=now->rc;
	}
	}
	int main()
	{
	n=re();
	nul=new Fhq_Treap(0,0,0,0,0);
	rot=rx=ry=rz=nul;
	while(n--)
	{
	int op=re(),k=re();
	if(op==1)
	{
	split(rot,k,rx,ry);
	rot=merge(merge(rx,new_(k)),ry);
	}
	if(op==2)
	{
	split(rot,k,rx,rz);
	split(rx,k-1,rx,ry);
	ry=merge(ry->lc,ry->rc);
	rot=merge(merge(rx,ry),rz);
	}
	if(op==3)
	{
	split(rot,k-1,rx,ry);
	wr(rx->siz+1),putchar('\n');
	rot=merge(rx,ry);
	}
	if(op==4)wr(kth(rot,k)),putchar('\n');
	if(op==5)
	{
	split(rot,k-1,rx,ry);
	wr(kth(rx,rx->siz)),putchar('\n');
	rot=merge(rx,ry);
	}
	if(op==6)
	{
	split(rot,k,rx,ry);
	wr(kth(ry,1)),putchar('\n');
	rot=merge(rx,ry);
	}
	}
	return 0;
	}

	void split(int i,int k,int &x,int &y)
	{
	if(!i){x=y=0;return;}
	if(T[i].tag)pushdown(i);
	if(k<=T[T[i].lc].siz)y=i,split(T[i].lc,k,x,T[i].lc);
	else x=i,split(T[i].rc,k-T[T[i].lc].siz-1,T[i].rc,y);
	pushup(i);
	}

	void pushdown(int i)
	{
	swap(T[i].lc,T[i].rc);
	T[T[i].lc].tag^=1;
	T[T[i].rc].tag^=1;
	T[i].tag=0;
	}

	const int inf=1e5+7;
	int n,m;
	struct Fhq_Treap{
	int lc,rc;
	int siz,val;
	unsigned pri;
	bool tag;
	}T[inf];
	int cnt,rot,rx,ry,rz;
	#include<random>
	mt19937 rnd(51205);
	int new_(int k)
	{
	T[++cnt].pri=rnd();
	T[cnt].siz=1;T[cnt].val=k;
	return cnt;
	}
	void pushup(int i)
	{
	T[i].siz=T[T[i].lc].siz+T[T[i].rc].siz+1;
	}
	void pushdown(int i)
	{
	swap(T[i].lc,T[i].rc);
	T[T[i].lc].tag^=1;
	T[T[i].rc].tag^=1;
	T[i].tag=0;
	}
	void split(int i,int k,int &x,int &y)
	{
	if(!i){x=y=0;return;}
	if(T[i].tag)pushdown(i);
	if(k<=T[T[i].lc].siz)y=i,split(T[i].lc,k,x,T[i].lc);
	else x=i,split(T[i].rc,k-T[T[i].lc].siz-1,T[i].rc,y);
	pushup(i);
	}
	int merge(int x,int y)
	{
	if(!x\|\|!y)return x\|y;
	if(T[x].pri<T[y].pri)
	{
	if(T[x].tag)pushdown(x);
	T[x].rc=merge(T[x].rc,y);
	pushup(x);return x;
	}
	else
	{
	if(T[y].tag)pushdown(y);
	T[y].lc=merge(x,T[y].lc);
	pushup(y);return y;
	}
	}
	void dfs(int i)
	{
	if(T[i].tag)pushdown(i);
	if(T[i].lc)dfs(T[i].lc);
	wr(T[i].val),putchar(' ');
	if(T[i].rc)dfs(T[i].rc);
	}
	int main()
	{
	n=re();m=re();
	for(int i=1;i<=n;i++)
	rot=merge(rot,new_(i));
	for(int i=1;i<=m;i++)
	{
	int l=re(),r=re();
	split(rot,r,rx,rz);
	split(rx,l-1,rx,ry);
	T[ry].tag^=1;
	rot=merge(merge(rx,ry),rz);
	}
	dfs(rot);
	return 0;
	}

	int n,m,k;
	struct Fhq_Treap{
	int siz,val,sum,tag;
	unsigned pri;
	Fhq_Treap lc,rc;
	Fhq_Treap(int siz,int val,int sum,int tag,unsigned pri,Fhq_Treap* lc,Fhq_Treap* rc):
	siz(siz),val(val),sum(sum),tag(tag),pri(pri),lc(lc),rc(rc){}
	}rot,rx,ry,rz,*nul;
	#include<random>
	mt19937 rnd(51205);
	Fhq_Treap* new_(int k)
	{
	return new Fhq_Treap(1,k,k,0,rnd(),nul,nul);
	}
	void pushup(Fhq_Treap* &i)
	{
	i->siz=i->lc->siz+i->rc->siz+1;
	i->sum=i->lc->sum+i->rc->sum+i->val;
	}
	void pushdown(Fhq_Treap* &i)
	{
	i->lc->val+=i->tag;i->lc->tag+=i->tag;
	i->rc->val+=i->tag;i->rc->tag+=i->tag;
	i->lc->sum+=i->tag*i->lc->siz;
	i->rc->sum+=i->tag*i->rc->siz;
	i->tag=0;
	}
	void split(Fhq_Treap* i,int k,Fhq_Treap* &x,Fhq_Treap* &y)
	{
	if(i==nul){x=y=nul;return;}
	if(i->tag)pushdown(i);
	if(k<=i->lc->siz)y=i,split(i->lc,k,x,i->lc);
	else x=i,split(i->rc,k-i->lc->siz-1,i->rc,y);
	pushup(i);
	}
	Fhq_Treap* merge(Fhq_Treap* x,Fhq_Treap* y)
	{
	if(x==nul)return y;
	if(y==nul)return x;
	if(x->pri<y->pri)
	{
	if(x->tag)pushdown(x);
	x->rc=merge(x->rc,y);
	pushup(x);return x;
	}
	else
	{
	if(y->tag)pushdown(y);
	y->lc=merge(x,y->lc);
	pushup(y);return y;
	}
	}
	void update(int l,int r,int k)
	{
	split(rot,r,rx,rz);
	split(rx,l-1,rx,ry);
	ry->val+=k,ry->tag+=k;
	ry->sum+=k*ry->siz;
	rot=merge(merge(rx,ry),rz);
	}
	int ask(int l,int r)
	{
	split(rot,r,rx,rz);
	split(rx,l-1,rx,ry);
	int ret=ry->sum;
	rot=merge(merge(rx,ry),rz);
	return ret;
	}
	int main()
	{
	n=re();m=re();
	nul=new Fhq_Treap(0,0,0,0,0,0,0);
	rot=rx=ry=rz=nul;
	for(int i=1;i<=n;i++)
	k=re(),rot=merge(rot,new_(k));
	while(m--)
	{
	int op=re(),l=re(),r=re();
	if(op==1)update(l,r,re());
	else wr(ask(l,r)),putchar('\n');
	}
	return 0;
	}

	bool pd(int i)
	{
	if(i==T[T[i].fa].hz[0])return 0;//左儿子
	else return 1;//右儿子
	}

	void rotate(int i)
	{
	int fa=T[i].fa,gf=T[fa].fa;
	int pdi=pd(i),pdf=pd(fa);
	T[i].fa=gf;if(gf)T[gf].hz[pdf]=i;
	T[fa].hz[pdi]=T[i].hz[pdi^1];
	if(T[i].hz[pdi^1])T[T[i].hz[pdi^1]].fa=fa;
	T[i].hz[pdi^1]=fa;T[fa].fa=i;
	pushup(fa),pushup(i);
	}

	void pushup(int i)
	{
	T[i].siz=T[T[i].hz[0]].siz+T[T[i].hz[1]].siz+T[i].cnt;
	}

	void spaly(int i,int to)
	{
	to=T[to].fa;
	while(T[i].fa^to)rotate(i);
	if(!to)rot=i;
	}

	void splay(int i,int to)
	{
	to=T[to].fa;
	int fa=T[i].fa;
	while(fa!=to)
	{
	if(T[fa].fa==to){rotate(i);break;}//最后一步单旋
	if(pd(i)^pd(fa))rotate(i);//之字形
	else rotate(fa);//一字型
	rotate(i);fa=T[i].fa;//最后一步都是旋 i
	}
	if(!to)rot=i;
	}

晓看天色暮看云

平衡树

Fhq_Treap

基本概念与储存

实现权值平衡树

分裂-split

合并-merge

其他操作

1. pushup

2. new_ k

3. insert k

4. remove k

5. ask_kth

6. ask_rank k

7. ask_pre/ask_nex k

完整代码

指针版实现

实现区间平衡树

建树

分裂-split

翻转-reverse

AC Code

指针实现

其他操作

Splay

基本概念与储存

树旋转

单旋

伸展（双旋）

实现权值平衡树

插入-insert

排名-rank

k 小值-kth

前驱、后继-pre/nex

删除-remove

AC Code

实现区间平衡树

AC Code

其他操作

可持久化

公告

搜索

常用链接

随笔档案

1. `pushup`

2. `new_ k`

3. `insert k`

4. `remove k`

5. `ask_kth`

6. `ask_rank k`

7. `ask_pre/ask_nex k`

	void splay(int i,int to)
	{
	to=T[to].fa;
	for(int fa=T[i].fa;fa!=to;rotate(i),fa=T[i].fa)
	if(T[fa].fa^to)rotate((pd(i)^pd(fa))?i:fa);
	if(!to)rot=i;
	}

	int new_(int k,int fa)
	{
	T[++cnt].fa=fa,T[cnt].val=k;
	T[cnt].siz=T[cnt].cnt=1;
	return cnt;
	}

	void insert(int k)
	{
	if(!rot){rot=new_(k,0);return;}
	int now=rot,fa=0;
	while(now)
	{
	if(k==T[now].val)
	{
	T[now].siz++,T[now].cnt++;
	splay(now,rot);return;
	}
	fa=now;
	if(k<T[now].val)now=T[now].hz[0];
	else now=T[now].hz[1];
	}
	now=new_(k,fa);
	T[fa].hz[k>T[fa].val]=now;
	splay(now,rot);
	}

	int ask_rnk(int k)
	{
	int now=rot,ans=0;
	while(now)
	{
	if(k==T[now].val)
	{
	int ret=T[T[now].hz[0]].siz;
	splay(now,rot);
	return ans+ret+1;
	}
	if(k<T[now].val)now=T[now].hz[0];
	else ans+=T[T[now].hz[0]].siz+T[now].cnt,now=T[now].hz[1];
	}
	return ans+1;
	}

	int ask_kth(int k)
	{
	int now=rot;
	while(1)
	{
	if(T[T[now].hz[0]].siz+1<=k&&k<=T[T[now].hz[0]].siz+T[now].cnt)
	{splay(now,rot);return T[now].val;}
	if(k<=T[T[now].hz[0]].siz)now=T[now].hz[0];
	else k-=T[T[now].hz[0]].siz+T[now].cnt,now=T[now].hz[1];
	}
	}

	int pre()
	{
	int now=T[rot].hz[0];
	if(now)
	{
	while(T[now].hz[1])
	now=T[now].hz[1];
	splay(now,rot);
	}
	return now;
	}
	int ask_pre(int k)
	{
	insert(k);int ret=T[pre()].val;
	remove(k);return ret;
	}
	int nex()
	{
	int now=T[rot].hz[1];
	if(now)
	{
	while(T[now].hz[0])
	now=T[now].hz[0];
	splay(now,rot);
	}
	return now;
	}
	int ask_nex(int k)
	{
	insert(k);int ret=T[nex()].val;
	remove(k);return ret;
	}

	void remove(int k)
	{
	ask_rnk(k);int now=rot;
	if(T[now].cnt>1){T[now].cnt--,T[now].siz--;return;}
	if(T[now].hz[0]+T[now].hz[1]==0){clear(now),rot=0;return;}
	if(T[now].hz[0]==0)
	{
	rot=T[now].hz[1];T[rot].fa=0;
	pushup(rot);return;
	}
	if(T[now].hz[1]==0)
	{
	rot=T[now].hz[0];T[rot].fa=0;
	pushup(rot);return;
	}
	int ls=pre();
	splay(ls,rot);
	T[rot].hz[1]=T[now].hz[1];
	T[T[now].hz[1]].fa=rot;
	clear(now);pushup(rot);
	}

	const int inf=1e5+7;
	int n;
	struct Splay{
	int fa,hz[2];
	int siz,cnt,val;
	}T[inf],q0;
	int rot,cnt;
	void clear(int i){T[i]=q0;}
	void pushup(int i){T[i].siz=T[T[i].hz[0]].siz+T[T[i].hz[1]].siz+T[i].cnt;}
	bool pd(int i){return i==T[T[i].fa].hz[1];}
	void rotate(int i)
	{
	int fa=T[i].fa,gf=T[fa].fa;
	int pdi=pd(i),pdf=pd(fa);
	T[i].fa=gf;if(gf)T[gf].hz[pdf]=i;
	T[fa].hz[pdi]=T[i].hz[pdi^1];
	if(T[i].hz[pdi^1])T[T[i].hz[pdi^1]].fa=fa;
	T[i].hz[pdi^1]=fa;T[fa].fa=i;
	pushup(fa),pushup(i);
	}
	void splay(int now,int to)
	{
	to=T[to].fa;
	for(int fa=T[now].fa;fa!=to;rotate(now),fa=T[now].fa)
	if(T[fa].fa^to)rotate((pd(now)^pd(fa))?now:fa);
	if(!to)rot=now;
	}
	int new_(int k,int fa)
	{
	T[++cnt].fa=fa,T[cnt].val=k;
	T[cnt].siz=T[cnt].cnt=1;
	return cnt;
	}
	void insert(int k)
	{
	if(!rot){rot=new_(k,0);return;}
	int now=rot,fa=0;
	while(now)
	{
	if(k==T[now].val)
	{
	T[now].siz++,T[now].cnt++;
	splay(now,rot);return;
	}
	fa=now;
	if(k<T[now].val)now=T[now].hz[0];
	else now=T[now].hz[1];
	}
	now=new_(k,fa);
	T[fa].hz[k>T[fa].val]=now;
	splay(now,rot);
	}
	int ask_rnk(int k)
	{
	int now=rot,ans=0;
	while(now)
	{
	if(k==T[now].val)
	{
	int ret=T[T[now].hz[0]].siz;
	splay(now,rot);
	return ans+ret+1;
	}
	if(k<T[now].val)now=T[now].hz[0];
	else ans+=T[T[now].hz[0]].siz+T[now].cnt,now=T[now].hz[1];
	}
	return ans+1;
	}
	int ask_kth(int k)
	{
	int now=rot;
	while(1)
	{
	if(T[T[now].hz[0]].siz+1<=k&&k<=T[T[now].hz[0]].siz+T[now].cnt)
	{splay(now,rot);return T[now].val;}
	if(k<=T[T[now].hz[0]].siz)now=T[now].hz[0];
	else k-=T[T[now].hz[0]].siz+T[now].cnt,now=T[now].hz[1];
	}
	}
	int pre()
	{
	int now=T[rot].hz[0];
	if(now)
	{
	while(T[now].hz[1])
	now=T[now].hz[1];
	splay(now,rot);
	}
	return now;
	}
	int nex()
	{
	int now=T[rot].hz[1];
	if(now)
	{
	while(T[now].hz[0])
	now=T[now].hz[0];
	splay(now,rot);
	}
	return now;
	}
	void remove(int k)
	{
	ask_rnk(k);int now=rot;
	if(T[now].cnt>1){T[now].cnt--,T[now].siz--;return;}
	if(T[now].hz[0]+T[now].hz[1]==0){clear(now),rot=0;return;}
	if(T[now].hz[0]==0)
	{
	rot=T[now].hz[1];T[rot].fa=0;
	pushup(rot);return;
	}
	if(T[now].hz[1]==0)
	{
	rot=T[now].hz[0];T[rot].fa=0;
	pushup(rot);return;
	}
	int ls=pre();
	splay(ls,rot);
	T[rot].hz[1]=T[now].hz[1];
	T[T[now].hz[1]].fa=rot;
	clear(now);pushup(rot);
	}
	int ask_pre(int k)
	{
	insert(k);int ret=T[pre()].val;
	remove(k);return ret;
	}
	int ask_nex(int k)
	{
	insert(k);int ret=T[nex()].val;
	remove(k);return ret;
	}
	int main()
	{
	n=re();
	for(int i=1;i<=n;i++)
	{
	int op=re(),k=re();
	if(op==1)insert(k);
	if(op==2)remove(k);
	if(op==3)wr(ask_rnk(k)),putchar('\n');
	if(op==4)wr(ask_kth(k)),putchar('\n');
	if(op==5)wr(ask_pre(k)),putchar('\n');
	if(op==6)wr(ask_nex(k)),putchar('\n');
	}
	return 0;
	}

	const int inf=1e5+7;
	int n,m,a[inf];
	struct Splay{
	int fa,hz[2];
	int siz,val,tag;
	}T[inf];
	int rot,cnt;
	void pushup(int i){T[i].siz=T[T[i].hz[0]].siz+T[T[i].hz[1]].siz+1;}
	bool pd(int i){return T[T[i].fa].hz[1]==i;}
	void build(int &i,int l,int r,int fa)
	{
	if(l>r)return;
	int mid=(l+r)>>1;i=++cnt;
	T[i].val=a[mid];
	T[i].fa=fa;T[i].siz=1;
	build(T[i].hz[0],l,mid-1,i);
	build(T[i].hz[1],mid+1,r,i);
	pushup(i);
	}
	void rotate(int i)
	{
	int fa=T[i].fa,gf=T[fa].fa;
	int pdi=pd(i),pdf=pd(fa);
	T[i].fa=gf;if(gf)T[gf].hz[pdf]=i;
	if(T[i].hz[pdi^1])T[T[i].hz[pdi^1]].fa=fa;
	T[fa].hz[pdi]=T[i].hz[pdi^1];
	T[fa].fa=i;T[i].hz[pdi^1]=fa;
	pushup(fa),pushup(i);
	}
	void splay(int i,int to)
	{
	for(int fa=T[i].fa;fa!=to;rotate(i),fa=T[i].fa)
	if(T[fa].fa^to)rotate((pd(i)^pd(fa))?i:fa);
	if(!to)rot=i;
	}
	void pushdown(int i)
	{
	T[T[i].hz[0]].tag^=1;
	T[T[i].hz[1]].tag^=1;
	swap(T[i].hz[0],T[i].hz[1]);
	T[i].tag=0;
	}
	int ask_kth(int k)
	{
	int i=rot;
	while(1)
	{
	if(T[i].tag)pushdown(i);
	if(k==T[T[i].hz[0]].siz+1)return i;
	if(k<=T[T[i].hz[0]].siz)i=T[i].hz[0];
	else k-=T[T[i].hz[0]].siz+1,i=T[i].hz[1];
	}
	}
	void reverse(int l,int r)
	{
	l=ask_kth(l),r=ask_kth(r);
	splay(l,0);splay(r,l);
	int pos=T[rot].hz[1];
	pos=T[pos].hz[0];
	T[pos].tag^=1;
	}
	void dfs(int now)
	{
	if(!now)return;
	if(T[now].tag)pushdown(now);
	dfs(T[now].hz[0]);
	if((T[now].val^-1)&(T[now].val^inf))
	wr(T[now].val),putchar(' ');
	dfs(T[now].hz[1]);
	}
	int main()
	{
	n=re();m=re();
	a[1]=-1,a[n+2]=inf;
	for(int i=1;i<=n;i++)a[i+1]=i;
	build(rot,1,n+2,0);
	for(int i=1;i<=m;i++)
	{
	int l=re()+1,r=re()+1;
	reverse(l-1,r+1);
	}
	dfs(rot);
	return 0;
	}