分块九讲

（别问我为什么鸽了这么久）

一些闲话

忽然好想学分块~~

LOJ 我来了！！！

~~要不是 Ynoi 做不动 qwq~~

题目 link

什么是分块

严格来讲，分块是一种思想，而非一种数据结构，又被称为“优雅的暴力”。

顾名思义，分块就是将一整个数组分成若干块的小数组，便于维护一些信息。

至于分多少块，一般来说，不能过多，也不能过少。

太少的话，会有大量的时间浪费在零散的块处理；

太多的话，对于整块的处理有会很繁琐，失去了分块的意义。

块状数组的建立

确定块长。

大多数情况下都是取 \(\sqrt n\) 的（毕竟是暴力，不需要太完美；但如果是 Ynoi 当我没说）。至于其他情况，可查看徐明宽在 2017 年的国家集训队论文《非常规大小分块算法初探》。
确定块的左右端点

块左端点为上一个块右端点 +1，右端点即为当前块编号乘块长。
维护块内信息

比如所属区间和区间和等内容。

len=sqrt(n);//1. 块长
for(int i=1;i<=len;i++)
	L[i]=R[i-1]+1,R[i]=i*len;//2. 块端点
R[len]=n;
for(int i=1;i<=len;i++)
	for(int j=L[i];j<=R[i];j++)
		bel[j]=i;//3. 所属区间

对于块内外的处理

大体上来说就是“大段维护，小段朴素”

具体操作根据题目灵活多变（真 · 灵活）。

而某些区间操作，可能有“懒标”

对，就是线段树的懒标。~~虽然但是，我习惯这样叫~~

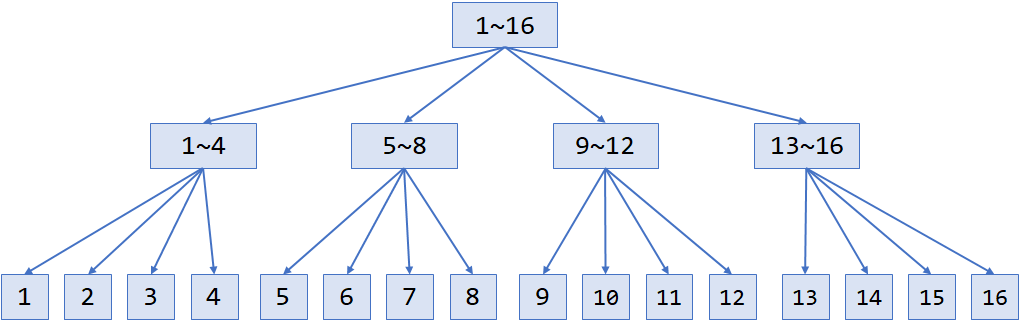
那么也就可以用另一种方式理解分块：

线段树是深度为 \(\log\) 的树形结构，分块就是深度为 3 的树形结构：

（图片来源于知乎，侵权自删）

时间复杂度分析

（由于能力限制，只分析块长为 \(\sqrt n\) 的情况）

对于零散块的处理，最长不过 \(\sqrt n\)，同样，整块的块数也不超过 \(\sqrt n\)。

所以单次维护的时间复杂度为 \(O(\sqrt n)\) 的。

那么 m 次操作的时间复杂度就是 \(O(m\sqrt n)\)。

当然，也会有单次操作会带一个 \(\log\)，此时需要另作讨论。

分块九讲

上述介绍可能比较笼统，对于没接触过分块的人不怎么友好。

接下来将会有九个分块经典入门题来带领读者进一步领略分块的优雅。

心急的童鞋可以快进到分块 9。

分块 1

题意概述：区间加，单点求值。

会线段树 / 树状数组的应该一眼就能秒了，但我们学分块，就强制用分块来做。

初始化和之上所述基本没有变化。此时的块内信息需要维护区间和。（其实并不需要）

for(int i=1;i<=len;i++)
	for(int j=L[i];j<=R[i];j++)
		bel[j]=i,sum[i]+=a[j];

区间加时，分两种情况讨论（大多数分块都会这样讨论）：

修改区间的左右端点在同一块内

此时直接对此块暴力加即可。
```
if(lin==rin)
{
	for(int i=l;i<=r;i++)
		a[i]+=k,sum[lin]+=k;
	return;
}
```
lin 和 rin 分别为左右端点所在的块内。

修改区间的左右端点不在同一块内

对于两边的零散区间，按照上述进行暴力处理，而中间的整块，加上懒标即可。

for(int i=l;i<=R[lin];i++)//左边的零散块
	sum[lin]+=k,a[i]+=k;
for(int i=L[rin];i<=r;i++)//右边的零散块
	sum[rin]+=k,a[i]+=k;
for(int i=lin+1;i<rin;i++)//中间的整块
	tag[i]+=k;

这样，查询时只需要将值与区间的懒标相加即可。

完整代码：

const int inf=5e4+7;
int n,len,a[inf];
int L[400],R[400],bel[inf];
int sum[400],tag[400];
void update(int l,int r,int k)
{
	int lin=bel[l],rin=bel[r];
	if(lin==rin)
	{
		for(int i=l;i<=r;i++)
			a[i]+=k,sum[lin]+=k;
		return;
	}
	for(int i=l;i<=R[lin];i++)
		sum[lin]+=k,a[i]+=k;
	for(int i=L[rin];i<=r;i++)
		sum[rin]+=k,a[i]+=k;
	for(int i=lin+1;i<rin;i++)
		tag[i]+=k;
}
int ask(int x)
{
	return a[x]+tag[bel[x]];
}
int main()
{
	n=re();len=sqrt(n);
	for(int i=1;i<=n;i++)
		a[i]=re();
	for(int i=1;i<=len;i++)
		L[i]=R[i-1]+1,R[i]=i*len;
	R[len]=n;
	for(int i=1;i<=len;i++)
		for(int j=L[i];j<=R[i];j++)
			bel[j]=i,sum[i]+=a[j];
	for(int i=1;i<=n;i++)
	{
		int op=re(),l=re(),r=re(),k=re();
		if(op==0)update(l,r,k);
		else wr(ask(r)),putchar('\n');
	}
	return 0;
}

分块 2

题意概述：区间加，区间查询小于某个数的个数。

对于一个无序数组而言，查询小于某数的个数需要的复杂度是 \(O(n)\) 的。而对于有序数组而言，则可以通过二分查找达到 \(O(\log n)\) 的复杂度。

因此我们在预处理时将每个块内的元素进行排序，这样就可以通过二分较为快速的求出整块内的小于某数的个数。

for(int i=1;i<=len;i++)
{
	for(int j=L[i];j<=R[i];j++)
		bel[j]=i,h[i].push_back(a[j]);
	sort(h[i].begin(),h[i].end());
}

对于零散块，仅有某些数会增加，因此顺序会发生改变。需要暴力修改，重新排序后再二分查找。

（为方便实现，此处的二分查找使用 lower_bound 实现）

void baoli(int l,int r,int k)
{//暴力修改
	int in=bel[l];
	for(int i=l;i<=r;i++)a[i]+=k;
	h[in].clear();
	for(int i=L[in];i<=R[in];i++)
		h[in].push_back(a[i]);
	sort(h[in].begin(),h[in].end());
}
int query(int l,int r,int k)
{//暴力查询
	vector<int>ls;
	for(int i=l;i<=r;i++)
		ls.push_back(a[i]+tag[bel[l]]);
	sort(ls.begin(),ls.end());
	return lower_bound(ls.begin(),ls.end(),k)-ls.begin();
}

而对于整块，注意到，整块区间加时，并不会影响其中元素的相对顺序。所以只需要更新懒标即可。区间查询直接二分即可。

void update(int l,int r,int k)
{//区间修改
	int lin=bel[l],rin=bel[r];
	if(lin==rin)
	{
		baoli(l,r,k);
		return;
	}
	baoli(l,R[lin],k);
	baoli(L[rin],r,k);
	for(int i=lin+1;i<rin;i++)
		tag[i]+=k;
}
int ask(int l,int r,int k)
{//区间查询
	int lin=bel[l],rin=bel[r];
	if(lin==rin)return query(l,r,k);
	int ans=0;
	ans+=query(l,R[lin],k)+query(L[rin],r,k);
	for(int i=lin+1;i<rin;i++)
		ans+=lower_bound(h[i].begin(),h[i].end(),k-tag[i])-h[i].begin();
	return ans;
}

完整代码：

const int inf=5e4+7;
int n,len,a[inf];
int bel[inf],L[400],R[400];
int tag[400];
vector<int>h[400];
void baoli(int l,int r,int k)
{
	int in=bel[l];
	for(int i=l;i<=r;i++)a[i]+=k;
	h[in].clear();
	for(int i=L[in];i<=R[in];i++)
		h[in].push_back(a[i]);
	sort(h[in].begin(),h[in].end());
}
void update(int l,int r,int k)
{
	int lin=bel[l],rin=bel[r];
	if(lin==rin)
	{
		baoli(l,r,k);
		return;
	}
	baoli(l,R[lin],k);
	baoli(L[rin],r,k);
	for(int i=lin+1;i<rin;i++)
		tag[i]+=k;
}
int query(int l,int r,int k)
{
	vector<int>ls;
	for(int i=l;i<=r;i++)
		ls.push_back(a[i]+tag[bel[l]]);
	sort(ls.begin(),ls.end());
	return lower_bound(ls.begin(),ls.end(),k)-ls.begin();
}
int ask(int l,int r,int k)
{
	int lin=bel[l],rin=bel[r];
	if(lin==rin)return query(l,r,k);
	int ans=0;
	ans+=query(l,R[lin],k)+query(L[rin],r,k);
	for(int i=lin+1;i<rin;i++)
		ans+=lower_bound(h[i].begin(),h[i].end(),k-tag[i])-h[i].begin();
	return ans;
}
int main()
{
	n=re();len=sqrt(n);
	for(int i=1;i<=n;i++)
		a[i]=re();
	for(int i=1;i<=len;i++)
		L[i]=R[i-1]+1,R[i]=i*len;
	R[len]=n;
	for(int i=1;i<=len;i++)
	{
		for(int j=L[i];j<=R[i];j++)
			bel[j]=i,h[i].push_back(a[j]);
		sort(h[i].begin(),h[i].end());
	}
	for(int i=1;i<=n;i++)
	{
		int op=re(),l=re(),r=re(),k=re();
		if(op==0)update(l,r,k);
		else wr(ask(l,r,k*k)),putchar('\n');
	}
	return 0;
}

分块 3

题意概述：区间加，区间查询某个数的前驱。

和“分块 2”相同，对有序数组查询前驱较为简单。因此本题的思路和“分块 2”基本无异，只是细节实现上存在不同。

对于整块，区间加同样不会影响相对顺序，只需要用 tag 记录。对于零散块，可以暴力重排之后再二分查找。

完整代码：

const int inf=1e5+7;
int n,len,a[inf];
int bel[inf],L[400],R[400];
int tag[400];
vector<int>h[400];
void baoli(int l,int r,int k)
{
	int in=bel[l];
	for(int i=l;i<=r;i++)
		a[i]+=k;
	h[in].clear();
	for(int i=L[in];i<=R[in];i++)
		h[in].push_back(a[i]);
	sort(h[in].begin(),h[in].end());
}
void update(int l,int r,int k)
{
	int lin=bel[l],rin=bel[r];
	if(lin==rin)
	{
		baoli(l,r,k);
		return;
	}
	baoli(l,R[lin],k);
	baoli(L[rin],r,k);
	for(int i=lin+1;i<rin;i++)
		tag[i]+=k;
}
int query(int l,int r,int k)
{
	vector<int>ls;
	for(int i=l;i<=r;i++)
		ls.push_back(a[i]+tag[bel[l]]);
	sort(ls.begin(),ls.end());
	vector<int>::iterator ret=lower_bound(ls.begin(),ls.end(),k);
	if(ret==ls.begin())return -1;
	return *--ret;
}
int ask(int l,int r,int k)
{
	int lin=bel[l],rin=bel[r];
	if(lin==rin)return query(l,r,k);
	int ans=-1;
	ans=max(ans,query(l,R[lin],k));
	ans=max(ans,query(L[rin],r,k));
	for(int i=lin+1;i<rin;i++)
	{
		vector<int>::iterator ls=lower_bound(h[i].begin(),h[i].end(),k-tag[i]);
		if(ls==h[i].begin())ans=max(ans,-1);
		else ans=max(ans,*--ls+tag[i]);
	}
	return ans;
}
int main()
{
	n=re();len=sqrt(n);
	for(int i=1;i<=n;i++)
		a[i]=re();
	for(int i=1;i<=len;i++)
		L[i]=R[i-1]+1,R[i]=i*len;
	R[len]=n;
	for(int i=1;i<=len;i++)
	{
		for(int j=L[i];j<=R[i];j++)
			bel[j]=i,h[i].push_back(a[j]);
		sort(h[i].begin(),h[i].end());
	}
	for(int i=1;i<=n;i++)
	{
		int op=re(),l=re(),r=re(),k=re();
		if(op)wr(ask(l,r,k)),putchar('\n');
		else update(l,r,k);
	}
	return 0;
}

分块 4

题意概述：区间加，区间求和。

和“分块 1”相比，仅仅是将单点求值改为了区间求和。对比单点求值与区间求和的线段树，便可很容易写出此题的代码：

const int inf=1e5+7;
int n,len,a[inf];
int bel[inf],L[400],R[400];
int sum[400],tag[400];
void update(int l,int r,int k)
{
	int lin=bel[l],rin=bel[r];
	if(lin==rin)
	{
		for(int i=l;i<=r;i++)
			a[i]+=k,sum[lin]+=k;
		return;
	}
	for(int i=l;i<=R[lin];i++)
		a[i]+=k,sum[lin]+=k;
	for(int i=L[rin];i<=r;i++)
		a[i]+=k,sum[rin]+=k;
	for(int i=lin+1;i<rin;i++)
		tag[i]+=k,sum[i]+=k*(R[i]-L[i]+1);
}
int ask(int l,int r,int p)
{
	int lin=bel[l],rin=bel[r],ans=0;
	if(lin==rin)
	{
		for(int i=l;i<=r;i++)
			ans=(ans+a[i]+tag[lin])%p;
		return ans;
	}
	for(int i=l;i<=R[lin];i++)
		ans=(ans+a[i]+tag[lin])%p;
	for(int i=L[rin];i<=r;i++)
		ans=(ans+a[i]+tag[rin])%p;
	for(int i=lin+1;i<rin;i++)
		ans=(ans+sum[i])%p;
	return ans;
}
signed main()
{
	n=re();len=sqrt(n);
	for(int i=1;i<=n;i++)
		a[i]=re();
	for(int i=1;i<=len;i++)
		L[i]=R[i-1]+1,R[i]=i*len;
	R[len]=n;
	for(int i=1;i<=len;i++)
		for(int j=L[i];j<=R[i];j++)
			bel[j]=i,sum[i]+=a[j];
	for(int i=1;i<=n;i++)
	{
		int op=re(),l=re(),r=re(),k=re();
		if(op)wr(ask(l,r,k+1)),putchar('\n');
		else update(l,r,k);
	}
	return 0;
}

分块 5

题意概述：区间开方，区间求和。

很多人可能感觉这道题很眼熟，没错，就是这个。

相比较于之前的题目，其实这个题更为简单。

考虑开方这个操作有什么特点。没错，\(\sqrt 1=1\)。而 int 范围内的任何数，开方不到 10 次就会变成 1。

因此，如果一个块的数全是 1，开方时就可以直接跳过此块。虽然开始的时候，能跳过的块基本没有，但是随着操作次数的增加，全为 1 的块越来越多，跳过的也越来越多。

时间复杂度需要势能分析。

完整代码：

const int inf=5e4+7;
int n,len,a[inf];
int bel[inf],L[400],R[400];
int sum[400];
void update(int l,int r)
{
	int lin=bel[l],rin=bel[r];
	if(lin==rin)
	{
		for(int i=l;i<=r;i++)
			sum[lin]-=a[i],a[i]=sqrt(a[i]),sum[lin]+=a[i];
		return;
	}
	for(int i=l;i<=R[lin];i++)
		sum[lin]-=a[i],a[i]=sqrt(a[i]),sum[lin]+=a[i];
	for(int i=L[rin];i<=r;i++)
		sum[rin]-=a[i],a[i]=sqrt(a[i]),sum[rin]+=a[i];
	for(int i=lin+1;i<rin;i++)
	{
		if(sum[i]==R[i]-L[i]+1)continue;
		sum[i]=0;
		for(int j=L[i];j<=R[i];j++)
			a[j]=sqrt(a[j]),sum[i]+=a[j];
	}
}
int ask(int l,int r)
{
	int lin=bel[l],rin=bel[r],ans=0;
	if(lin==rin)
	{
		for(int i=l;i<=r;i++)
			ans+=a[i];
		return ans;
	}
	for(int i=l;i<=R[lin];i++)
		ans+=a[i];
	for(int i=L[rin];i<=r;i++)
		ans+=a[i];
	for(int i=lin+1;i<rin;i++)
		ans+=sum[i];
	return ans;
}
int main()
{
	n=re();len=sqrt(n);
	for(int i=1;i<=n;i++)
		a[i]=re();
	for(int i=1;i<=len;i++)
		L[i]=R[i-1]+1,R[i]=i*len;
	R[len]=n;
	for(int i=1;i<=len;i++)
		for(int j=L[i];j<=R[i];j++)
			bel[j]=i,sum[i]+=a[j];
	for(int i=1;i<=n;i++)
	{
		int op=re(),l=re(),r=re(),k=re();
		if(op)wr(ask(l,r)),putchar('\n');
		else update(l,r);
	}
	return 0;
}

分块 6

题意概述：单点插入，单点查询。

对于整个 vector 的单点插入复杂度是 \(O(n)\) 的，但是如果有 \(\sqrt n\) 个 vector，复杂度就变成了 \(O(\sqrt n)\)。

具体思路就是，将整个数组分块。通过 vector 可以很容易的得到当前块的元素个数，那么通过遍历每个块，就能用 \(O(\sqrt n)\) 的复杂度找到要插入的位置（查询同理）。块中插入直接用 vector 自带的 insert 就好。

完整代码：

const int inf=1e5+7;
int n,len,a[inf];
int L[400],R[400];
vector<int>h[inf];
void insert(int id,int k)
{
	for(int i=1;i<=len;i++)
	{
		if(id<=h[i].size())
		{
			vector<int>::iterator ls=h[i].begin()+id-1;
			h[i].insert(ls,k);
			return;
		}
		id-=h[i].size();
	}
}
int ask(int id)
{
	for(int i=1;i<=len;i++)
	{
		if(id<=h[i].size())
			return *(h[i].begin()+id-1);
		id-=h[i].size();
	}
}
int main()
{
	n=re();len=sqrt(n);
	for(int i=1;i<=n;i++)
		a[i]=re();
	for(int i=1;i<=len;i++)
		L[i]=R[i-1]+1,R[i]=i*len;
	R[len]=n;
	for(int i=1;i<=len;i++)
		for(int j=L[i];j<=R[i];j++)
			h[i].push_back(a[j]);
	for(int i=1;i<=n;i++)
	{
		int op=re(),l=re(),r=re(),k=re();
		if(op)wr(ask(r)),putchar('\n');
		else insert(l,r);
	}
	return 0;
}

分块 7

题意概述：区间乘，区间加，单点查询。

类似于线段树 2 的模板。在“分块 1”时，我们就已经使用了懒标，那么本题我们同样也可以和线段树 2 一样，使用两个懒标。

同样是局部暴力整体维护，注意 mul 标记的优先级是要高于 add 的。记得取模。

const int inf=1e5+7,mod=10007;
int n,len,a[inf];
int bel[inf],L[400],R[400];
int add[400],mul[400];
void baoli_add(int l,int r,int k)
{
	int in=bel[l];
	for(int i=L[in];i<=R[in];i++)
		a[i]=((a[i]*mul[in])%mod+add[in])%mod;
	add[in]=0,mul[in]=1;
	for(int i=l;i<=r;i++)
		a[i]=(a[i]+k)%mod;
}
void update_add(int l,int r,int k)
{
	int lin=bel[l],rin=bel[r];
	if(lin==rin)
	{
		baoli_add(l,r,k);
		return;
	}
	baoli_add(l,R[lin],k);
	baoli_add(L[rin],r,k);
	for(int i=lin+1;i<rin;i++)
		add[i]=(add[i]+k)%mod;
}
void baoli_mul(int l,int r,int k)
{
	int in=bel[l];
	for(int i=L[in];i<=R[in];i++)
		a[i]=((a[i]*mul[in])%mod+add[in])%mod;
	add[in]=0,mul[in]=1;
	for(int i=l;i<=r;i++)
		a[i]=(a[i]*k)%mod;
}
void update_mul(int l,int r,int k)
{
	int lin=bel[l],rin=bel[r];
	if(lin==rin)
	{
		baoli_mul(l,r,k);
		return;
	}
	baoli_mul(l,R[lin],k);
	baoli_mul(L[rin],r,k);
	for(int i=lin+1;i<rin;i++)
		mul[i]=(mul[i]*k)%mod,add[i]=(add[i]*k)%mod;
}
int main()
{
	n=re();len=sqrt(n);
	for(int i=1;i<=n;i++)
		a[i]=re();
	for(int i=1;i<=len;i++)
		L[i]=R[i-1]+1,R[i]=i*len,mul[i]=1;
	R[len]=n;
	for(int i=1;i<=len;i++)
		for(int j=L[i];j<=R[i];j++)
			bel[j]=i;
	for(int i=1;i<=n;i++)
	{
		int op=re(),l=re(),r=re(),k=re()%mod;
		if(op==0)update_add(l,r,k);
		if(op==1)update_mul(l,r,k);
		if(op==2)wr(((a[r]*mul[bel[r]])%mod+add[bel[r]])%mod),putchar('\n');
	}
	return 0;
}

分块 8

题意概述：区间查询相同值并推平。

区间推平容易实现，通过 tag 记录整块被推平的数，零散块下放 tag 并暴力修改即可。

而查询时，对于零散块，同样下放标记并暴力统计；对于整块，每个块开一个 map 作桶，记录每个数出现的次数。推平的时候就把整块的桶 clear，并为推平的值赋为块长，查询的时候也只需要查询当前块的桶。

完整代码：

const int inf=1e5+7;
int n,len,a[inf];
int bel[inf],L[400],R[400];
int tag[400],vis[400];
map<int,int>T[400];
int baoli(int l,int r,int k)
{
	int in=bel[l],ans=0;
	if(vis[in])
	{
		vis[in]=0;
		for(int i=L[in];i<=R[in];i++)
			a[i]=tag[in];
	}
	for(int i=l;i<=r;i++)
	{
		T[in][a[i]]--;T[in][k]++;
		ans+=(a[i]==k),a[i]=k;
	}
	return ans;
}
int assign(int l,int r,int k)
{
	int lin=bel[l],rin=bel[r],ans=0;
	if(lin==rin)return baoli(l,r,k);
	ans+=baoli(l,R[lin],k)+baoli(L[rin],r,k);
	for(int i=lin+1;i<rin;i++)
	{
		ans+=T[i][k];vis[i]=1,tag[i]=k;
		T[i].clear();T[i][k]=R[i]-L[i]+1;
	}
	return ans;
}
int main()
{
	n=re();len=sqrt(n);
	for(int i=1;i<=n;i++)
		a[i]=re();
	for(int i=1;i<=len;i++)
		L[i]=R[i-1]+1,R[i]=i*len;
	R[len]=n;
	for(int i=1;i<=len;i++)
		for(int j=L[i];j<=R[i];j++)
			bel[j]=i,T[i][a[j]]++;
	for(int i=1;i<=n;i++)
	{
		int l=re(),r=re(),k=re();
		wr(assign(l,r,k)),putchar('\n');
	}
	return 0;
}

分块 9

题意概述：查询区间众数。

一道很经典的分块 / 莫队的题。

分块

首先可以想到，既然是众数，就要统计出现次数，也就是要用到桶。

通过桶，可以统计每个块内的众数。

但是知道每个块内的众数有什么用呢？并没有。

由于只有 \(\sqrt n\) 个块，我们可以通过 \(O(n\sqrt n)\) 的复杂度用一个二维数组统计两个块之间所有数的众数。很容易证明，这样不会炸空间。

代码实现：

for(int i=1;i<=len;i++)
{
	memset(T,0,sizeof(T));
	int zs=0,maxn=0;
	for(int j=L[i];j<=n;j++)
	{
		T[a[j]]++;
		if((maxn<T[a[j]])||(maxn==T[a[j]]&&zs>a[j]))
			maxn=T[a[j]],zs=a[j];
		Z[i][bel[j]]=zs;
	}
}

由于值域比较大，数据已经过离散化。

显然啊，如果将一个整个区间分成三个区间，那么整个区间的众数要么在中间的整块里，要么在两边的零散块里。

中间整块的众数我们已经处理出来了，但是不知道作为众数的出现次数。

两边的零散块可以暴力找数，但是需要一个较快的方法找出现次数。

考虑二分。在离散化的时候，将每个数出现的位置存到相应的 vector 中。

最后在找数的出现次数时，便可直接二分查找区间的左右端点，来找到当前数在区间里的出现次数。

代码如下：

int times(int l,int r,int k)
{
	auto sta_=lower_bound(h[k].begin(),h[k].end(),l);
	auto end_=upper_bound(h[k].begin(),h[k].end(),r);
	return end_-sta_;
}
int ask(int l,int r)
{
	int lin=bel[l],rin=bel[r];
	int zs=0,sum=0;
	if(lin==rin)
	{
		memset(T,0,sizeof(T));
		for(int i=l;i<=r;i++)
		{
			T[a[i]]++;
			if((sum<T[a[i]])||(sum==T[a[i]]&&zs>a[i]))
				sum=T[a[i]],zs=a[i];
		}
		return zs;
	}
	zs=Z[lin+1][rin-1];sum=times(l,r,zs);
	for(int i=l;i<=R[lin];i++)
	{
		int ls=times(l,r,a[i]);
		if((sum<ls)||(sum==ls&&zs>a[i]))
			sum=ls,zs=a[i];
	}
	for(int i=L[rin];i<=r;i++)
	{
		int ls=times(l,r,a[i]);
		if((sum<ls)||(sum==ls&&zs>a[i]))
			sum=ls,zs=a[i];
	}
	return zs;
}

最后，将查找的众数再通过离散化数组找到原数据即可。

完整代码：

const int inf=1e5+7;
int n,m,len,a[inf],bok[inf];
int bel[inf],L[400],R[400];
vector<int>h[inf];
int T[inf],Z[400][400];
int times(int l,int r,int k)
{
	auto sta_=lower_bound(h[k].begin(),h[k].end(),l);
	auto end_=upper_bound(h[k].begin(),h[k].end(),r);
	return end_-sta_;
}
int ask(int l,int r)
{
	int lin=bel[l],rin=bel[r];
	int zs=0,sum=0;
	if(lin==rin)
	{
		memset(T,0,sizeof(T));
		for(int i=l;i<=r;i++)
		{
			T[a[i]]++;
			if((sum<T[a[i]])||(sum==T[a[i]]&&zs>a[i]))
				sum=T[a[i]],zs=a[i];
		}
		return zs;
	}
	zs=Z[lin+1][rin-1];sum=times(l,r,zs);
	for(int i=l;i<=R[lin];i++)
	{
		int ls=times(l,r,a[i]);
		if((sum<ls)||(sum==ls&&zs>a[i]))
			sum=ls,zs=a[i];
	}
	for(int i=L[rin];i<=r;i++)
	{
		int ls=times(l,r,a[i]);
		if((sum<ls)||(sum==ls&&zs>a[i]))
			sum=ls,zs=a[i];
	}
	return zs;
}
int main()
{
	n=re();len=sqrt(n);
	for(int i=1;i<=n;i++)
		bok[i]=a[i]=re();
	sort(bok+1,bok+n+1);
	int num=unique(bok+1,bok+n+1)-bok-1;
	for(int i=1;i<=n;i++)
	{
		a[i]=lower_bound(bok+1,bok+num+1,a[i])-bok;
		h[a[i]].push_back(i);
	}
	for(int i=1;i<=len;i++)
		L[i]=R[i-1]+1,R[i]=i*len;
	R[len]=n;
	for(int i=1;i<=len;i++)
		for(int j=L[i];j<=R[i];j++)
			bel[j]=i;
	for(int i=1;i<=len;i++)
	{
		memset(T,0,sizeof(T));
		int zs=0,maxn=0;
		for(int j=L[i];j<=n;j++)
		{
			T[a[j]]++;
			if((maxn<T[a[j]])||(maxn==T[a[j]]&&zs>a[j]))
				maxn=T[a[j]],zs=a[j];
			Z[i][bel[j]]=zs;
		}
	}
	for(int i=1;i<=n;i++)
	{
		int l=re(),r=re();
		wr(bok[ask(l,r)]),putchar('\n');
	}
	return 0;
}

莫队

莫队的多种类型已经在这篇博客中写过，本题属于回滚莫队中的不删除莫队。

代码：

const int inf=2e5+7;
int n,len,a[inf],bok[inf];
int bel[inf],L[500],R[500];
struct Query{
	int le,ri,id;
	bool operator <(const Query &b)const
	{
		return (bel[le]^bel[b.le])?(le<b.le):(ri<b.ri);
	}
}h[inf];
int T[inf],baoli[inf];
int maxn,zs,ans_[inf];
signed main()
{
	n=re();len=sqrt(n);
	for(int i=1;i<=n;i++)
		bok[i]=a[i]=re();
	sort(bok+1,bok+n+1);
	int num=unique(bok+1,bok+n+1)-bok-1;
	for(int i=1;i<=n;i++)
		a[i]=lower_bound(bok+1,bok+num+1,a[i])-bok;
	for(int i=1;i<=len;i++)
		L[i]=R[i-1]+1,R[i]=L[i]+len-1;
	R[len]=n;
	for(int i=1;i<=len;i++)
		for(int j=L[i];j<=R[i];j++)
			bel[j]=i;
	for(int i=1;i<=n;i++)
		h[i].le=re(),h[i].ri=re(),h[i].id=i;
	sort(h+1,h+n+1);
	int i=1;
	for(int k=1;k<=len;k++)
	{
		if(bel[h[i].le]^k)continue;
		memset(T,0,sizeof(T));
		int ir=R[k],il=R[k]+1;
		maxn=0,zs=0;
		while(bel[h[i].le]==k)
		{
			if(bel[h[i].ri]==k)
			{
				int lsmax=0,lszs=0;
				for(int j=h[i].le;j<=h[i].ri;j++)
				{
					baoli[a[j]]++;
					if(lsmax<baoli[a[j]]||(lsmax==baoli[a[j]]&&lszs>a[j]))
						lszs=a[j],lsmax=baoli[a[j]];
				}
				ans_[h[i].id]=bok[lszs];
				for(int j=h[i].le;j<=h[i].ri;j++)
					baoli[a[j]]=0;
				i++;continue;
			}
			while(ir<h[i].ri)
			{
				ir++,T[a[ir]]++;
				if(maxn<T[a[ir]]||(maxn==T[a[ir]]&&zs>a[ir]))
					zs=a[ir],maxn=T[a[ir]];
			}
			int lastmax=maxn,lastzs=zs,hg=il;
			while(il>h[i].le)
			{
				il--,T[a[il]]++;
				if(maxn<T[a[il]]||(maxn==T[a[il]]&&zs>a[il]))
					zs=a[il],maxn=T[a[il]];
			}
			ans_[h[i].id]=bok[zs];
			while(il<hg)T[a[il]]--,il++;
			maxn=lastmax;zs=lastzs;i++;
		}
	}
	for(int i=1;i<=n;i++)
		wr(ans_[i]),putchar('\n');
	return 0;
}

posted @ 2022-08-17 20:36 Zvelig1205 阅读(178) 评论(1) 编辑收藏举报

刷新页面返回顶部

Zvelig1205

晓看天色暮看云

分块九讲

分块九讲

一些闲话

什么是分块

块状数组的建立

对于块内外的处理

时间复杂度分析

分块九讲

分块 1

分块 2

分块 3

分块 4

分块 5

分块 6

分块 7

分块 8

分块 9

公告