不等式专项

重要不等式

$a^2+b^2\ge 2ab$

当且仅当 $a=b$ 时等号成立。

例 1
在 $\Delta ABC$ 中，$\angle B=\dfrac{\pi}{3},b=2$，求 $S_{\Delta ABC}$ 面积的最大值。

解：

由余弦定理推论：$\cos B=\dfrac{a^2+c^2-4}{2ac}=\dfrac12$

$a^2+c^2-4=ac\ge 2ac-4$

$ac\le4$

则 $S=\dfrac12ac\sin B\le\sqrt3$

基本不等式

$a\ge0,b\ge0\Rightarrow\dfrac{a+b}{2}\ge\sqrt{ab}$

当且仅当 $a=b$ 时等号成立。

例 2
若 $a,b>0$，且 $a+b=1$，求 $\dfrac{1}{4a}+\dfrac{1}{9b}$ 的最小值。

解：

$\begin{array}{ll} \dfrac{1}{4a}+\dfrac{1}{9b} &=1\times(\dfrac{1}{4a}+\dfrac{1}{9b})\\ &=(a+b)\times(\dfrac{1}{4a}+\dfrac{1}{9b})\\ &=\dfrac{1}{4}+\dfrac{1}{9}+\dfrac{b}{4a}+\dfrac{a}{9b}\\ &\ge\dfrac{13}{36}+2\sqrt{\dfrac{b}{4a}\times\dfrac{a}{9b}}\\ &=\dfrac{25}{36} \end{array}$

糖水不等式

$a>b>0,m>0\Rightarrow\dfrac{b}{a}<\dfrac{b+m}{a+m}$

理解：在糖水中加糖，糖水变甜。

例 3
数列 $a_n=\dfrac{3^n-1}{2}$，求证 $\displaystyle\sum_{i=1}^n\dfrac{1}{a_i}<\dfrac32$

证明：

$\dfrac{1}{a_n}=\dfrac2{3^n-1}<\dfrac{2+1}{3^n-1+1}=\dfrac{3}{3^n}=3^{1-n}$

令 $b_n=3^{1-n}$

则 $\{b_n\}$ 首项 $\dfrac{1}{a_1}=1$，公比为 $3^{-1}$

$\displaystyle\sum_{i=1}^n\dfrac{1}{a_i}<\displaystyle\sum_{i=1}^nb_i=S_n=1\times\dfrac{1-3^{-n}}{1-3^{-1}}<\dfrac32$

故 $\displaystyle\sum_{i=1}^n\dfrac{1}{a_i}<\dfrac32$

$Q.E.D.$

均值不等式

$a>0,b>0\Rightarrow\dfrac{2}{\frac1a+\frac1b}\le\sqrt{ab}\le\dfrac{a+b}{2}\le\sqrt{\dfrac{a^2+b^2}{2}}$

当且仅当 $a=b$ 时等号成立。

拓展：

$\text{调和均值：}H_{n}=\dfrac{n}{\displaystyle\sum_{i=1}^{n}\dfrac{1}{x_{i}}}= \dfrac{n}{\dfrac{1}{x_{1}}+ \dfrac{1}{x_{2}}+ \cdots + \dfrac{1}{x_{n}}} \\$

$\text{几何均值：}G_{n}=\sqrt[n]{\displaystyle\prod_{i=1}^{n}x_{i}}= \sqrt[n]{x_{1}x_{2}\cdots x_{n}} \\$

$\text{算数均值：}A_{n}=\dfrac{1}{n}\displaystyle\sum_{i=1}^{n}x_{i}=\dfrac{x_{1}+ x_{2}+ \cdots + x_{n}}{n} \\$

$\text{平方均值：}Q_{n}=\sqrt{\dfrac{1}{n}\displaystyle\sum_{i=1}^{n}x_{i}^{2}}= \sqrt{\dfrac{x_{1}^{2}+ x_{2}^{2}+ \cdots + x_{n}^{2}}{n}} \\$

$H_{n}\leq G_{n}\leq A_{n}\leq Q_{n}$

当且仅当 $a_1=a_2=\cdots =a_n$ 时等号成立。

例 4
若 $x,y,z>0,xyz+y+z=12$，求 $\log_4x+\log_2y+\log_2z$ 的最大值。

解：

$\begin{array}{ll} \log_4x+\log_2y+\log_2z &=\log_4x+\log_4y^2+\log_4z^2\\ &=\log_4xy^2z^2\\ &\le\log_4(\dfrac{xyz+y+z}3)^3\\ &=3 \end{array}$

幂平均不等式

$\alpha>\beta\Rightarrow (\dfrac1n\displaystyle\sum_{i=1}^na^{\alpha})^{\frac1{\alpha}}\ge(\dfrac1n\displaystyle\sum_{i=1}^nb^{\beta})^{\frac1{\beta}}$

例 5
若 $x\in[0,\frac{\pi}{2}]$，求 $\sqrt{\sin x}+\sqrt{\cos x}$ 的最大值。

解：

$\begin{array}{rl} (\dfrac{\sqrt{\sin x}+\sqrt{\cos x}}2)^2&\le (\dfrac{\sin^2 x+\cos^2 x}2)^{\frac12}\\ &=(\dfrac12)^{\frac12}\\ \sqrt{\sin x}+\sqrt{\cos x}&\le 2\times (\dfrac12)^{\frac14}\\ &=2^{\frac34} \end{array}$

对数不等式

$a>0,b>0\Rightarrow\sqrt{ab}\le\dfrac{a-b}{\ln a -\ln b}\le\dfrac{a+b}{2}$

例 6
已知 $f(x)=x-a\ln x$，若 $f(x_1)=f(x_2)=k$，求证 $x_1+x_2>2a$。

证明：

$\because f(x_1)=f(x_2)$

$\therefore x_1-a\ln x_1=x_2-a\ln x_2$

$\therefore x_1-x_2=a\ln x_1-a\ln x_2$

$\therefore \dfrac{x_1-x_2}{a(\ln x_1-\ln x_2)}=1$

$\therefore \dfrac{x_1-x_2}{a(\ln x_1-\ln x_2)}=1<\dfrac{x_1+x_2}{2a}$

$\therefore x_1+x_2>2a$

$Q.E.D.$

绝对值的三角不等式

$||a|-|b||\le|a\pm b|\le|a|+|b|$

$a,b$ 可以是实数，复数，向量等。

例 7
已知函数 $f(x)=|x-a|+|x+3|$，若 $f(x)>-a$，求 $a$ 的取值范围。

解：

$f(x)=|x-a|+|x+3|\ge|x-a-x-3|=|-a-3|$

$\therefore f(x)_ {\min}=|-a-3|$

$\because f(x)>-a$

$\therefore f(x)_ {\min}>-a$

$\therefore |-a-3|>-a$

$\therefore (-a-3)^2>(-a)^2$

$\therefore a>-\dfrac32$

切线不等式

$e^x\ge x+1>x>x-1\ge\ln x$

当 $x=0$ 时前者等号成立，当 $x=1$ 时后者等号成立

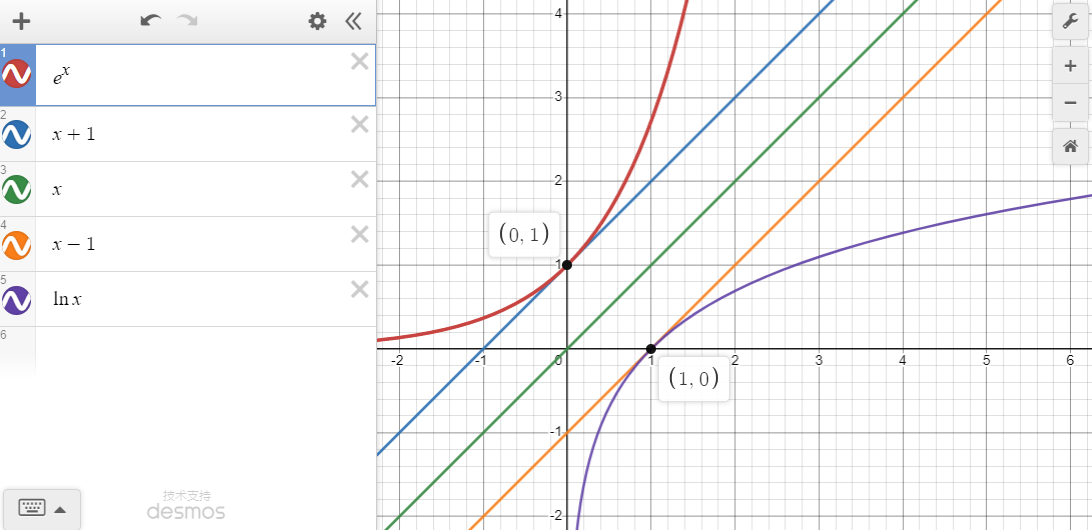
又名“方天画戟”

例 8
已知 $f(x)=e^x-\ln(x+m)$，当 $m\le2$ 时，求证 $f(x)>0$。

证明：

$f(x)=e^x-\ln(x+m)>(x+1)-(x+m-1)=2-m$

等号不同时成立，不取等

$\because m\le2$

$\therefore 2-m\ge0$

$\therefore f(x)>2-m\ge0$

$Q.E.D.$

柯西不等式

一般形式

$(\displaystyle\sum_{i=1}^na_i^2)(\displaystyle\sum_{i=1}^nb_i^2)\ge(\displaystyle\sum_{i=1}^na_ib_i)^2$

当且仅当 $\dfrac{a_1}{b_1}=\dfrac{a_2}{b_2}=\cdots=\dfrac{a_n}{b_n}$ 时等号成立

二维形式

$(a^2+b^2)(c^2+d^2)\ge(ac+bd)^2$

当且仅当 $\dfrac{a}{c}=\dfrac{b}{d}$ 时等号成立

推论 1

$\displaystyle\sum_{i=1}^na_i^2\ge\dfrac1n(\displaystyle\sum_{i=1}^na_i)^2$

当且仅当 $a_1=a_2=\cdots=a_n$ 时等号成立

推论 2

$\sqrt{(\displaystyle\sum_{i=1}^na_i^2)(\displaystyle\sum_{i=1}^nb_i^2)}\ge\displaystyle\sum_{i=1}^na_ib_i$

当且仅当 $\dfrac{a_1}{b_1}=\dfrac{a_2}{b_2}=\cdots=\dfrac{a_n}{b_n}$ 时等号成立

推广：赫尔德公式

$n\ge 2,p>1\text{且}\dfrac1p+\dfrac1q=1$

$(\displaystyle\sum_{i=1}^na_i^2)^{\frac1p}(\displaystyle\sum_{i=1}^nb_i^2)^{\frac1q}\ge\displaystyle\sum_{i=1}^na_ib_i$

当且仅当 $\dfrac{a_1}{b_1}=\dfrac{a_2}{b_2}=\cdots=\dfrac{a_n}{b_n}$ 时等号成立

例 9
已知 $x+y+z=1$，求 $(x-1)^2+(y+1)^2+(z+1)^2$ 的最小值。

解：

$(x-1)^2+(y+1)^2+(z+1)^2\ge\dfrac13[(x-1)+(y+1)+(z+1)]^2=\dfrac43$

权方和不等式

$a_i,b_i>0\Rightarrow\displaystyle\sum_{i=1}^n\dfrac{a_i^2}{b_i}\ge\dfrac{(\sum\limits_{i=1}^na_i)^2}{\sum\limits_{i=1}^nb_i}$

当且仅当 $\dfrac{a_1}{b_1}=\dfrac{a_2}{b_2}=\cdots=\dfrac{a_n}{b_n}$ 时等号成立

其实权方和不等式也是柯西不等式的推论

观察柯西不等式

$(\displaystyle\sum_{i=1}^na_i^2)(\displaystyle\sum_{i=1}^nb_i^2)\ge(\displaystyle\sum_{i=1}^na_ib_i)^2$

若 $a_i\to \dfrac{a_i}{\sqrt {b_i}},b_i\to\sqrt{b_i}$

$(\displaystyle\sum_{i=1}^n\dfrac{a_i^2}{b_i})(\displaystyle\sum_{i=1}^nb_i)\ge(\displaystyle\sum_{i=1}^n\dfrac{a_i}{\sqrt{b_i}}\sqrt{b_i})^2=(\displaystyle\sum_{i=1}^n a_i)^2$

$\displaystyle\sum_{i=1}^n\dfrac{a_i^2}{b_i}\ge\dfrac{(\displaystyle\sum_{i=1}^n a_i)^2}{(\displaystyle\sum_{i=1}^nb_i)}$

推广：

$a_i,b_i>0,m>0,\displaystyle\sum_{i=1}^n\dfrac{a_i^{m+1}}{b_i^m}\ge\dfrac{(\sum\limits_{i=1}^na_i)^{m+1}}{(\sum\limits_{i=1}^nb_i)^m}$

当且仅当 $\dfrac{a_1}{b_1}=\dfrac{a_2}{b_2}=\cdots=\dfrac{a_n}{b_n}$ 时等号成立

例 10
已知 $x+y=1,x>0,y>0$，求 $\dfrac1{x^2}+\dfrac8{y^2}$ 的最小值。

解：

$\dfrac1{x^2}+\dfrac8{y^2}=\dfrac{1^3}{x^2}+\dfrac{2^3}{y^2}\ge\dfrac{(1+2)^3}{(x+y)^2}=27$

排序不等式

若 $a_1\le a_2\le \cdots \le a_n$ 且 $b_1\le b_2\le \cdots \le b_n$

设 $\{t\}$ 是 ${1,2\cdots n}$ 的一个排列

则有 $a_1b_n+a_2b_{n-1}+\cdots a_nb_1\le a_1b_{t_1}+a_2b_{t_2}+\cdots+a_nb_{t_n}\le a_1b_1+a_2b_2+\cdots a_nb_n$

当且仅当 $a_1=a_2=\cdots=a_n$ 或 $b_1=b_2=\cdots=b_n$ 时等号成立

简记：$\text{反序和}\le\text{乱序和}\le\text{正序和}$

例 11
已知 $a,b,c,d>0$，求证：$a^ab^bc^cd^d>a^db^cc^bd^a$

证明：

要证 $a^ab^bc^cd^d>a^db^cc^bd^a$

即证 $\ln a^ab^bc^cd^d>\ln a^db^cc^bd^a$

即证 $a\ln a+b\ln b+c\ln c+d\ln d>d\ln a+c\ln b+b\ln c+a\ln d$

不妨设 $a\le b\le c\le d$，则显然 $\ln a\le\ln b\le\ln c\le\ln d$

由排序不等式，显然 $a\ln a+b\ln b+c\ln c+d\ln d>d\ln a+c\ln b+b\ln c+a\ln d$ 成立

故 $a^ab^bc^cd^d>a^db^cc^bd^a$

$Q.E.D.$

琴生不等式

若 $f(x)$ 在 $(a,b)$ 上为凸函数，则有 $x_1,x_2,\cdots,x_n\in(a,b)$，满足 $\dfrac1n\displaystyle\sum_{i=1}^nf(x_i)\le f(\dfrac1n\displaystyle\sum_{i=1}^nx_i)$

若 $g(x)$ 在 $(a,b)$ 上为凹函数，则有 $x_1,x_2,\cdots,x_n\in(a,b)$，满足 $\dfrac1n\displaystyle\sum_{i=1}^ng(x_i)\ge g(\dfrac1n\displaystyle\sum_{i=1}^nx_i)$

当且仅当 $x_1=x_2=\cdots=x_n$ 时等号成立

例 12
若 $a+2b=12$，求 $2^a+2^{b+1}$ 的最小值。

解：

$2^a+2^{b+1}=2^a+2^b+2^b$

令 $f(x)=2^x$，显然 $f(x)$ 是凹函数

$f(a)+f(b)+f(b)>3\times f(\dfrac{a+b+b}{3})=3\times f(4)=48$

$2^a+2^{b+1}>48$

伯努利不等式

若 $x_1,x_2,\cdots,x_n\in(-1,0)\cup(0,+\infty)$ 且同号

则 $(1+x_1)(1+x_2)\cdots(1+x_n)>1+x_1+x_2+\cdots+x_n$

推论：

$x\in(-1,0)\cup(0,+\infty),(1+x)^n>1+nx$

例 13
若 $e_n=(1+\dfrac1n)^n(n\in N_+)$，求证：数列 $\{e_n\}$ 严格递增。

证明：

$\begin{array}{ll} \dfrac{e_{n+1}}{e_n}&=\dfrac{(\frac{n+2}{n+1})^{n+1}}{(\frac{n+1}{n})^n}\\ &=(\dfrac{n+2}{n+1})[\dfrac{n(n+2)}{(n+1)^2}]^n\\ &=(\dfrac{n+2}{n+1})(\dfrac{n^2+2n}{n^2+2n+1})^n\\ &=(\dfrac{n+2}{n+1})[1-\dfrac{1}{(n+1)^2}]^n\\ &>(\dfrac{n+2}{n+1})[1-\dfrac{n}{(n+1)^2}]\\ &=(\dfrac{n+2}{n+1})[\dfrac{(n+1)^2-n}{(n+1)^2}]\\ &=\dfrac{(n+2)(n+1)^2-n(n+2)}{(n+1)^3}\\ &=\dfrac{n^3+3n^2+3n+2}{n^3+3n^2+3n+1}\\ &=1+\dfrac{1}{n^3+3n^2+3n+1}\\ &>1 \end{array}$

故 $e_{n+1}>e_n$

$Q.E.D.$

切比雪夫不等式

若随机变量 $X$ 有期望 $E(X)$ 和方差 $D(X)$，对于任意的正数 $\xi$，满足 $P(|X-E(X)|\ge\xi)\le\dfrac{D(X)}{\xi^2}$

例 14
已知正常男性成年人血液中每毫升白细胞数的平均值为 7300，标准差为 700，则每毫升血液中含有的白细胞数在 5200~9400 之间的概率。

解：

$\begin{array}{ll} P(5200\le X\le 9400)&=P(5200-7300\le X-7300\le 9400-7300)\\ &=P(|X-7300|\le2100)\\ &=1-P(|X-7300|\ge2100)\\ &\ge1-\dfrac{D(X)}{2100^2}\\ &=\dfrac89 \end{array}$

舒尔不等式

$a,b,c\ge0,r\in R\Rightarrow a^r(a-b)(a-c)+b^r(b-a)(b-c)+c^r(c-a)(c-b)\ge0$

当且仅当 $a=b=c$ 或 $a=b,c=0$ 时等号成立。

三次舒尔（$r=1$）：$a^3+b^3+c^3+3abc\ge a^2(b+c)+b^2(a+c)+c^2(a+b)$

四次舒尔（$r=2$）：$a^4+b^4+c^4+abc(a+b+c)\ge a^3(b+c)+b^3(a+c)+c^3(a+b)$

例 15
已知 $x,y,z\ge0,x+y+z=1$，求证 $0\le xy+yz+zx-2xyz\le\dfrac{7}{27}$

证明：

$xy+yz+zx-2xyz=y(x+z-2xz)+xz\ge y(2\sqrt{xz}-2xz)+xz\ge0$

由三次舒尔 $x^3+y^3+z^3+3xyz\ge x^2(y+z)+y^2(x+z)+z^2(x+y)$

$\therefore x^3+y^3+z^3+3xyz+3x^2y+3x^2z+3y^2x+3y^2z+3z^2x+3z^2y+12xyz\ge 4x^2y+4x^2z+4y^2x+4y^2z+4z^2x+4z^2y+12xyz$

即 $(x+y+z)^3+9xyz\ge 4(x+y+z)(xy+yz+zx)$

$\because x+y+z=1$

$\therefore 1+9xyz\ge 4(xy+yz+zx)$

$\therefore 1+xyz\ge 4(xy+yz+zx-2xyz)$

由均值不等式

$xyz\le(\dfrac{x+y+z}{3})^3=\dfrac1{27}$

$\therefore 4(xy+yz+zx-2xyz)\le\dfrac{28}{27}$

$\therefore xy+yz+zx-2xyz\le\dfrac{7}{27}$

故 $0\le xy+yz+zx-2xyz\le\dfrac{7}{27}$

$Q.E.D.$