莫队一本通
莫队
两只小手跳来跳去
众所周知,莫队算法是由莫涛大神总结的一种短小精悍的离线暴力维护区间操作的算法。
因其简短的框架,简单好记的板子和优雅的时间复杂度而闻名。

普通莫队
(本部分主要以莫队的二维理解为主)
基本思路
普通莫队就是最普通的莫队。
举个简单的例子:
对于给定的数列,k 次询问,每次输出区间 [l,r] 的区间和。
显然啊,这题可以直接前缀和。但既然是学莫队,那就强制用莫队做。
如果现在知道 \([2,5]\) 的区间和,怎么求区间 \([2,6]\) 的区间和?
显然,直接用前者 \(+a_6\) 就可以了。
莫队就是这样。莫队的核心就是在 \(O(1)\) 的时间里从状态 \([l,r]\) 转移到状态 \([l-1,r],[l+1,r],[l,r-1],[l,r+1]\) 其中之一。
就是开头说的两只小手跳来跳去。
等等。
如果将方括号换成圆括号的话……
那不就是从状态 \((l,r)\) 转移到状态 \((l-1,r),(l+1,r),(l,r-1),(l,r+1)\) 嘛。
那不就是以 \(l\) 为横坐标,\(r\) 为纵坐标的平面直角坐标系上的点吗?
就是这样:
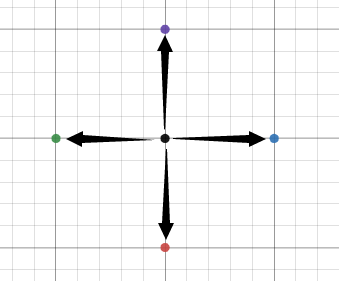
这就是莫队的二维理解。
举个例子:
比如我们要维护 \([1,4],[2,6],[3,5],[5,6]\) 四个区间,就相当于是坐标系上的 \((1,4),(2,6),(3,5),(5,6)\) 四个点。也就是:

而从一个点去到另一个点的花费就是两点的曼哈顿距离。
显然,我们要在较短的时间里完成所有的任务,那么就是要经历所有的点,且费用较小。
如果是最优,那显然是曼哈顿最小生成树,不过既然我们是暴力,那显然不用最优。
接下来思考:
如果按照询问顺序进行回答的话……
显然不行,比如我给你这样几个点:
\((1,2),(99999,100000),(1,2),(99999,100000)\cdots\)
那么你每次移动都要跑整个序列。累死两只小手
如果将所有的点储存下来,然后按左端点排序之后再依次遍历的话……
就是这样:
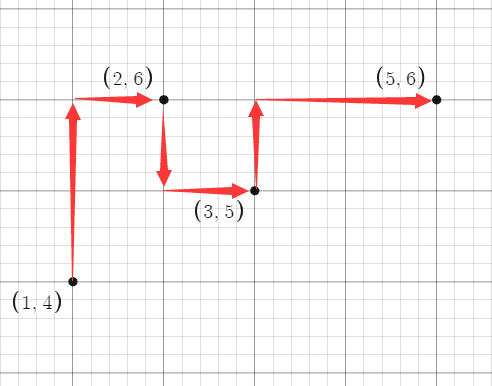
对于上边的的好像可以?
\((1,2),(1,2)\cdots(99999,100000),(99999,100000)\cdots\)
确实。
但还是不行。
为啥?
比如我给你这样的几个点:
\((1,10^5),(2,2),(3,10^5),(4,4)\cdots\)
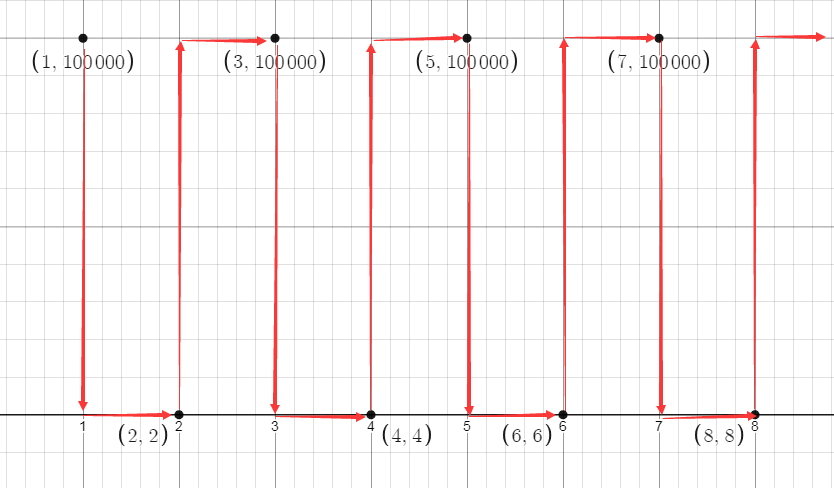
上上下下来来回回累死两个小手
不过这给我们了一个启示:不同的询问顺序,询问总时间也是不同的。
所以要对询问顺序进行优化。
以上便是莫队的前置知识。
至于优化方案……
将所有的点按照块长为 \(\sqrt n\) 进行分块,块外左端点块递增,块内右端点递增。
那么上例中每个块中就是递增的,逐步上跳总比来回跑快吧。
代码处理
先完善一下上述题面:
题面描述:
给定一个长度为 n 的数列,有 m 询问,每次询问输出区间 \([l,r]\) 中各个元素的和。
输入格式:
第一行两个整数 n,m,含义如上。
第二行 n 个数,表示原数列。
接下来 m 行,每行两个整数 [l,r],表示查找的区间。
数据范围:
\(n,m<10^5\)
首先进行分块
len=sqrt(n);
for(int i=1;i<=n;i++)
a[i]=re(),bel[i]=i/len+1;
然后我们要将所有的询问储存下来
for(int i=1;i<=m;i++)
h[i].le=re(),h[i].ri=re(),h[i].id=i;
sort(h.begin(),h.end());
其中 h 数组:
struct Query{
int le,ri,id;
bool operator <(const Query &b)const
{
return (bel[le]^bel[b.le])?(le<b.le):(ri<b.ri);
}
}h[inf];
然后两只小手跳来跳去。
int il=1,ir=0;
for(int i=0;i<m;i++)
{
Query ls=h[i];
while(il>ls.le)insert(--il);
while(il<ls.le)remove(il++);
while(ir<ls.ri)insert(++ir);
while(ir>ls.ri)remove(ir--);
ans_[ls.id]=ans;
}
这里的 ++ -- 是不是很恶心的样子?
但其实很容易理解。
很容易想到,insert 需要先移动到目标位置再插入,remove 则需要先删除再移动到下一位置。
而对于两只手来说,左手向右是删除,向左是插入;右手向左是删除,向右是插入。
自己体会一下,会发现这个是不需要背的。
而 insert 和 remove 函数就要根据题目进行推导(就像状态转移方程)
在这个题中就是这样:
void insert(int i){ans+=a[i];}
void remove(int i){ans-=a[i];}
再优化
- 手打快读快写
比 scanf 快点。
int re()
{
int s=0,f=1;char ch=getchar();
while(ch>'9'||ch<'0')
{
if(ch=='-')f=-1;
ch=getchar();
}
while(ch>='0'&&ch<='9')
s=s*10+ch-48,ch=getchar();
return s*f;
}
void wr(int s)
{
if(s<0)putchar('-'),s=-s;
if(s>9)wr(s/10);
putchar(s%10+48);
}
当然也有比我的更快的,这个只是我习惯的。
- 奇偶优化
别人说奇偶优化是玄学,可我感觉奇偶优化是艺术。
顾名思义,奇偶优化就是按照块的奇偶性进行优化。将奇数块内部按照右端点递增,偶数块内部按照右端点递减,块外按左端点递增进行排序。
(奇数块递减,偶数块递增也是可以的。)
刚刚是块内部逐步上跳,但是块与块之间是直接下来的,花费较大。但这时我们是逐步上跳,再逐步下跳。花费就更小了。
operator 就这样打:
bool operator <(const Query &b)const
{
return (bel[le]==bel[b.le])?((bel[le]&1)?(ri<b.ri):(ri>b.ri)):(le<b.le);
}
- 常数优化
将
while(il>ls.le)insert(--il);
while(il<ls.le)remove(il++);
while(ir<ls.ri)insert(++ir);
while(ir>ls.ri)remove(ir--);
和
void insert(int i){ans+=a[i];}
void remove(int i){ans-=a[i];}
压缩成
while(il>ls.le)ans+=a[--il];
while(il<ls.le)ans-=a[il++];
while(ir<ls.ri)ans+=a[++ir];
while(ir>ls.ri)ans-=a[ir--];
或者加上 inline 和 register。
例题
假设新加进来的袜子的颜色为 c,且现在颜色为 c 的袜子有 t 个。
根据排列组合知识,加入之前拿到相同颜色袜子的组合有 \(C_t^2\) 种,加入之后为 \(C_{t+1}^2\),则应该有:
同理可知,删除时有 \(ans=ans-(t-1)\)。
则 insert 和 remove 就好写了:
void insert(int i){ans+=T[a[i]]++;}
void remove(int i){ans-=--T[a[i]];}
其他的套板子就好了。
带修莫队
通过上面叙述可知,莫队是强制离线算法。
那么对于带修莫队要怎样实现呢?
回想莫队的二维理解,我们可以再引入一条时间轴,然后在分块排序的时候按照以下原则进行排序:
- 左端点不同块:左端点递增。
- 左端点同块,右端点不同块:右端点递增。
- 左右端点均同块:修改时间递增。
然后就相当于是从状态 \([l,r,t]\) 转移到状态 \([l,r,t-1],[l,r,t+1],[l-1,r,t],[l+1,r,t],[l,r-1,t],[l,r+1,t]\) 之一。
值得注意的是,对于要更改的点在查询的区间内的情况,还要顺带着将统计的答案更新。
例题
const int inf=1e6+7;
int n,m,len,ans;
int a[inf],T[inf];
int ans_[inf],bel[inf];
int cntQ,cntR;
struct Query{
int le,ri,tim,id,val;
bool operator <(const Query &b)const
{
return (bel[le]^bel[b.le])?(le<b.le):((bel[ri]^bel[b.ri])?(ri<b.ri):(tim<b.tim));
}
}h[inf];
struct Change{
int pos,val;
}c[inf];
void insert(int i){if(!T[i])ans++;T[i]++;}
void remove(int i){T[i]--;if(!T[i])ans--;}
int main()
{
n=re();m=re();
len=pow(n,2.0/3);
for(int i=1;i<=n;i++)
a[i]=re(),bel[i]=i/len+1;
for(int i=1;i<=m;i++)
{
char op[10]="";scanf("%s",op);
int x=re(),y=re();
if(op[0]=='Q')
{
cntQ++;
h[cntQ].le=x,h[cntQ].ri=y;
h[cntQ].id=cntQ;h[cntQ].tim=cntR;
}
else c[++cntR]=(Change){x,y};
}
sort(h+1,h+cntQ+1);
int il=1,ir=0,nowc=0;
for(int i=1;i<=cntQ;i++)
{
Query ls=h[i];
while(nowc<ls.tim)
{
nowc++;
if(il<=c[nowc].pos&&c[nowc].pos<=ir)
{
remove(a[c[nowc].pos]);
insert(c[nowc].val);
}
swap(a[c[nowc].pos],c[nowc].val);
}
while(nowc>ls.tim)
{
if(il<=c[nowc].pos&&c[nowc].pos<=ir)
{
remove(a[c[nowc].pos]);
insert(c[nowc].val);
}
swap(a[c[nowc].pos],c[nowc].val);
nowc--;
}
while(il>ls.le)insert(a[--il]);
while(il<ls.le)remove(a[il++]);
while(ir<ls.ri)insert(a[++ir]);
while(ir>ls.ri)remove(a[ir--]);
ans_[ls.id]=ans;
}
for(int i=1;i<=cntQ;i++)
wr(ans_[i]),putchar('\n');
return 0;
}
时间复杂度分析
不会
块大小为 \(\sqrt[3]{nt}\) 可以达到最快的理论复杂度 \(O(\sqrt[3]{n^4t})\),证明如下
设分块大小为 \(a\),莫队算法时间复杂度主要为 \(t\) 轴移动,同 \(r\) 块 \(l,r\) 移动,\(l\) 块间的 \(r\) 移动三部分
\(t\) 轴移动的复杂度为 \(O(\dfrac{n^2t}{a^2})\),同 \(r\) 块 \(l,r\) 移动复杂度为 \(O(na)\),\(l\) 块间的 \(r\) 移动复杂度为 \(O(\dfrac{n^2}{a})\)
三个函数 \(\max\) 的最小值当 \(a\) 为 \(\sqrt[3]{nt}\) 取得,为 \(O(\sqrt[3]{n^4t})\)
上述内容摘抄自洛谷题解
树上莫队
树上莫队分为两种:
-
假树上莫队(维护子树)
-
莫队上树(维护路径)
假树上莫队
用时间戳将树变成一个序列,然后直接对序列套普通莫队。
时间戳
按照深度优先遍历的过程,以每个节点第一次被访问的顺序,依次给予这 \(N\) 个节点 \(1\sim N\) 的整数标记,该标记就被称为时间戳,记为 dfn。
摘抄自李煜东的《算法竞赛进阶指南》
显然,子树的时间戳是连续的,那么在对应序列里就是连续的。
const int inf=1e5+7;
int n,m,len,x;
int a[inf],bel[inf];
int fir[inf],nex[inf<<1],poi[inf<<1],cnt;
void ins(int x,int y)
{
nex[++cnt]=fir[x];
poi[cnt]=y;
fir[x]=cnt;
}
int siz[inf],dfn[inf],rnk[inf],sum;
void dfs(int now,int from)
{
siz[now]=1;
dfn[now]=++sum;rnk[sum]=now;
for(int i=fir[now];i;i=nex[i])
{
int p=poi[i];
if(p==from)continue;
dfs(p,now);
siz[now]+=siz[p];
}
}
struct Query{
int le,ri,id,k;
bool operator <(const Query &b)const
{
return (bel[le]^bel[b.le])?(le<b.le):((bel[le]&1)?(ri<b.ri):(ri>b.ri));
}
}h[inf];
int T[inf],kth[inf],ans_[inf];
void insert(int i){T[a[i]]++,kth[T[a[i]]]++;}
void remove(int i){kth[T[a[i]]]--,T[a[i]]--;}
int main()
{
n=re();m=re();len=sqrt(n);
for(int i=1;i<=n;i++)
a[i]=re(),bel[i]=i/len+1;
for(int i=1;i<n;i++)
{
int u=re(),v=re();
ins(u,v);ins(v,u);
}
dfs(1,1);
for(int i=1;i<=m;i++)
{
x=re();h[i].k=re();
h[i].le=dfn[x],h[i].ri=dfn[x]+siz[x]-1,h[i].id=i;
}
sort(h+1,h+m+1);
int il=1,ir=0;
for(int i=1;i<=m;i++)
{
while(il>h[i].le)insert(rnk[--il]);
while(il<h[i].le)remove(rnk[il++]);
while(ir<h[i].ri)insert(rnk[++ir]);
while(ir>h[i].ri)remove(rnk[ir--]);
ans_[h[i].id]=kth[h[i].k];
}
for(int i=1;i<=m;i++)
wr(ans_[i]),putchar('\n');
return 0;
}
某位大佬的话:事实上,子树上统计完全不需要莫队,传个标记就能 \(O(n\log n)\) 了。
没错,那个大佬也划掉了。
莫队上树
继续尝试用时间戳解决此题。
样例的树:
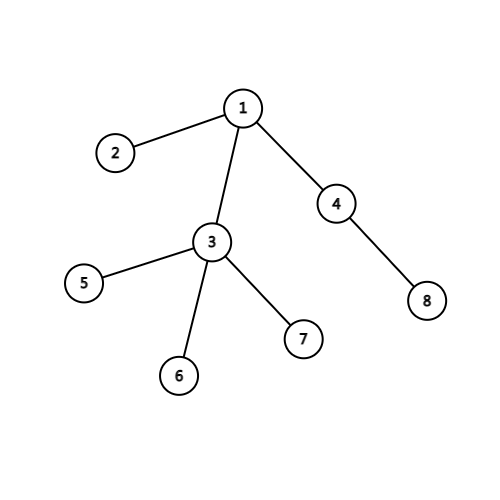
时间戳: [1,2,3,5,6,7,4,8]
查询路径:7~8
对应区…间……
玄学
看来用时间戳好像不能解决此题。
不过,我们还有 dfs 序!
树的 DFS 序
一般来讲,我们在对树进行深度优先遍历时,对于每个节点,在刚进入递归后以及即将回溯前各记录一次该点的编号,最后产生的长度为 \(2N\) 的节点序列就称为树的 DFS 序。
摘抄自李煜东的《算法竞赛进阶指南》
比如上图的 dfs 序即为:[1,2,3,5,5,6,6,7,7,3,4,8,8,4,1]
dfs 序有一些美妙的性质,比如
- 每个节点 x 的编号在 dfs 序中恰好出现两次。
- 设出现的位置分别为 \(sta_x\) 和 \(end_x\),那么闭区间 \([sta_x,end_x]\) 就是以 x 为根的子树的 dfs 序。
- 对于一条路径 {x,y}(假设 \(sta_x<sta_y\))而言,若 \(lca(x,y)=x\),则在路径上的点在区间 \([sta_x,sta_y]\) 中仅出现 1 次,而不在路径上的点在区间中出现 2 次或 0 次;否则,lca 在区间中出现 0 次。
根据这三点,尤其是第三点,维护链就变得相对容易了。
还是这个假设,对于一条路径 {x,y}(假设 \(sta_x<sta_y\))而言,若 \(lca(x,y)=x\),则直接维护区间 \([sta_x,sta_y]\);否则维护区间 \([end_x,sta_y]\) 并在统计答案时顺便维护 lca。
处理完这些,其他的套莫队板子就行了。用一个数组维护这个点是否在路经上,每出现一次就异或 1,然后在判断颜色数。
const int inf=1e5+7;
int n,m,bok[inf],a[inf];
int fir[inf],nex[inf<<1],poi[inf<<1],cnt;
void ins(int x,int y)
{
nex[++cnt]=fir[x];
poi[cnt]=y;
fir[x]=cnt;
}
int fa[inf][20],dep[inf];
int oul[inf<<1],sta_[inf],end_[inf],sum;
void dfs(int now,int from)
{
fa[now][0]=from;
dep[now]=dep[from]+1;
sta_[now]=++sum;oul[sum]=now;
for(int i=fir[now];i;i=nex[i])
{
int p=poi[i];
if(p==from)continue;
dfs(p,now);
}
end_[now]=++sum;oul[sum]=now;
}
int _lca(int x,int y)
{
if(dep[x]<dep[y])swap(x,y);
for(int i=19;i>=0;i--)
if(dep[fa[x][i]]>=dep[y])
x=fa[x][i];
if(x==y)return x;
for(int i=19;i>=0;i--)
if(fa[x][i]!=fa[y][i])
x=fa[x][i],y=fa[y][i];
return fa[x][0];
}
int bel[inf];
struct Query{
int le,ri,id,lca;
bool operator <(const Query &b)const
{
return (bel[le]^bel[b.le])?(le<b.le):((bel[le]&1)?(ri<b.ri):(ri>b.ri));
}
}h[inf];
int col[inf],T[inf];
int ans_[inf],ans;
void insert(int i)
{
if(col[a[oul[i]]]==0)ans++;
col[a[oul[i]]]++;
}
void remove(int i)
{
col[a[oul[i]]]--;
if(col[a[oul[i]]]==0)ans--;
}
void update(int i)
{
T[oul[i]]^=1;
T[oul[i]]?insert(i):remove(i);
}
int main()
{
n=re();m=re();
for(int i=1;i<=n;i++)
bok[i]=a[i]=re();
sort(bok+1,bok+n+1);
int num=unique(bok+1,bok+n+1)-bok-1;
for(int i=1;i<=n;i++)
a[i]=lower_bound(bok+1,bok+num+1,a[i])-bok;
for(int i=1;i<n;i++)
{
int u=re(),v=re();
ins(u,v),ins(v,u);
}
dfs(1,1);
for(int j=1;j<20;j++)
for(int i=1;i<=n;i++)
fa[i][j]=fa[fa[i][j-1]][j-1];
int len=sqrt(sum);
for(int i=1;i<=sum;i++)
bel[i]=i/len+1;
for(int i=1;i<=m;i++)
{
int x=re(),y=re();
if(sta_[x]>sta_[y])swap(x,y);
int lca=_lca(x,y);
if(x^lca)h[i].le=end_[x],h[i].ri=sta_[y],h[i].lca=lca;
else h[i].le=sta_[x],h[i].ri=sta_[y];
h[i].id=i;
}
sort(h+1,h+m+1);
int il=1,ir=0;
for(int i=1;i<=m;i++)
{
while(il>h[i].le)update(--il);
while(il<h[i].le)update(il++);
while(ir<h[i].ri)update(++ir);
while(ir>h[i].ri)update(ir--);
int ls=ans;
if(h[i].lca&&col[a[h[i].lca]]==0)ls++;
ans_[h[i].id]=ls;
}
for(int i=1;i<=m;i++)
wr(ans_[i]),putchar('\n');
return 0;
}
如果你 TLE 了,就检查一下自己的 len 和 bel,因为 dfs 序的长度是 \(2\times N\) 的。
虽然但是,这个细节处理不到位并不会影响答案的正确性,因为莫队的两个小手的排序只会影响速度就因为这个 T 了好久。
回滚莫队
虽然我谷有回滚莫队的模板,但大多数人更倾向于 ATcoder 的歴史の研究。
回滚莫队,应用于某些特殊的情景,比如插入操作很容易,但删除的复杂度很高;或者删除操作很容易,插入的时间复杂度却很高。
不删除莫队
以歴史の研究为例,插入操作很容易实现,直接将当前最大值和新的事件的重要度取 max 即可。
但删除……
将整个桶扫一遍?
\(O(n^2\sqrt n)\) 的时间复杂度让你原地升天。
那能不能不删除?
哎~ 还真能
和普通莫队一样,块外按照左端点排序,块内按右端点排序(注意!此处不能使用奇偶优化!)
对于左端点在同一块内的所有询问,左手赋值为当前块的右端点 +1,右手赋值为当前块右端点。
然后右手不断向右移(因为排过序了)。每次左手左移之前先将当前答案记录下来(记作 last),然后左手左移。待更新答案之后,再将左手右移并在移动过程中维护桶,最后再令 ans=last。
这样就成功避免了删除操作。
对于左右端点在同一块内,直接暴力统计即可。
const int inf=1e5+7;
int n,m,len,a[inf],bok[inf];
int bel[inf],L[400],R[400];
struct Query{
int le,ri,id;
bool operator <(const Query &b)const
{
return (bel[le]^bel[b.le])?(le<b.le):(ri<b.ri);
}
}h[inf];
int T[inf],baoli[inf];
int maxn,ans_[inf];
signed main()
{
n=re();m=re();len=sqrt(n);
for(int i=1;i<=n;i++)
bok[i]=a[i]=re();
sort(bok+1,bok+n+1);
int num=unique(bok+1,bok+n+1)-bok-1;
for(int i=1;i<=n;i++)
a[i]=lower_bound(bok+1,bok+num+1,a[i])-bok;
for(int i=1;i<=len;i++)
L[i]=R[i-1]+1,R[i]=L[i]+len-1;
R[len]=n;
for(int i=1;i<=len;i++)
for(int j=L[i];j<=R[i];j++)
bel[j]=i;
for(int i=1;i<=m;i++)
h[i].le=re(),h[i].ri=re(),h[i].id=i;
sort(h+1,h+m+1);
int i=1;
for(int k=1;k<=len;k++)
{
if(bel[h[i].le]^k)continue;
memset(T,0,sizeof(T));
int ir=R[k],il=R[k]+1;maxn=0;
while(bel[h[i].le]==k)
{
if(bel[h[i].ri]==k)
{
int ls=0;
for(int j=h[i].le;j<=h[i].ri;j++)
{
baoli[a[j]]++;
ls=max(ls,bok[a[j]]*baoli[a[j]]);
}
ans_[h[i].id]=ls;
for(int j=h[i].le;j<=h[i].ri;j++)
baoli[a[j]]=0;
i++;continue;
}
while(ir<h[i].ri)
{
ir++,T[a[ir]]++;
maxn=max(maxn,bok[a[ir]]*T[a[ir]]);
}
int last=maxn,hg=il;
while(il>h[i].le)
{
il--,T[a[il]]++;
maxn=max(maxn,bok[a[il]]*T[a[il]]);
}
ans_[h[i].id]=maxn;
while(il<hg)T[a[il]]--,il++;
maxn=last;i++;
}
}
for(int i=1;i<=m;i++)
wr(ans_[i]),putchar('\n');
return 0;
}
时间复杂度
对于每块中的右端点,最坏情况下要进行 \(O(n)\) 次移动,共 \(\sqrt n\) 个块。
对于每个左端点,最坏情况下要进行 \(O(\sqrt n)\) 次移动,共 \(n\) 个左端点。
对于暴力,最多维护长度为 \(\sqrt n\) 的块。
时间复杂度 \(O(n\sqrt n)\)。
不插入莫队
有只增不减的莫队,当然也有只减不增的喽。
显然,每删除一个数,若删除之后区间内没有了这个数,那么就在删除的数和当前 mex 之间取 min。
而插入一个数后 mex 很难确定,所以要尽量避免这个操作。
那么就可以先预处理出当前点到序列末尾的 mex,然后套回滚莫队板子。具体思路和不删除莫队差不多,不理解的可以看代码。
const int inf=2e5+7;
int n,m,len,maxn;
int a[inf],T[inf],baoli[inf];
int bel[inf],L[500],R[500];
int mex_[inf],mex,ans_[inf];
struct Query{
int le,ri,id;
bool operator <(const Query &b)const
{
return (bel[le]^bel[b.le])?(le<b.le):(ri>b.ri);
}
}h[inf];
int main()
{
n=re();m=re();
for(int i=1;i<=n;i++)
{
a[i]=re(),maxn=max(maxn,a[i]);
T[a[i]]++;
}
for(int i=0;i<=maxn+1;i++)
if(T[i]==0){mex=i;break;}
for(int i=1;i<=n;i++)
{
mex_[i]=mex;T[a[i]]--;
if(T[a[i]]==0&&a[i]<mex)mex=a[i];
}
len=sqrt(n);
for(int i=1;i<=len;i++)
L[i]=R[i-1]+1,R[i]=L[i]+len-1;
R[len]=n;
for(int i=1;i<=len;i++)
for(int j=L[i];j<=R[i];j++)
bel[j]=i;
for(int i=1;i<=m;i++)
h[i].le=re(),h[i].ri=re(),h[i].id=i;
sort(h+1,h+m+1);
int i=1;
for(int k=1;k<=len;k++)
{
if(bel[h[i].le]^k)continue;
int ir=n,il=L[k];mex=mex_[il];
memset(T,0,sizeof(T));
for(int i=il;i<=ir;i++)T[a[i]]++;
while(bel[h[i].le]==k)
{
if(bel[h[i].ri]==k)
{
int lsans,lsmax=0;
for(int j=h[i].le;j<=h[i].ri;j++)
baoli[a[j]]++,lsmax=max(lsmax,a[j]);
for(int j=0;j<=lsmax+1;j++)
if(baoli[j]==0){lsans=j;break;}
ans_[h[i].id]=lsans;
for(int j=h[i].le;j<=h[i].ri;j++)
baoli[a[j]]--;
i++;continue;
}
while(ir>h[i].ri)
{
T[a[ir]]--;
if(T[a[ir]]==0&&mex>a[ir])mex=a[ir];
ir--;
}
int last=mex,hg=il;
while(il<h[i].le)
{
T[a[il]]--;
if(T[a[il]]==0&&mex>a[il])mex=a[il];
il++;
}
ans_[h[i].id]=mex;
while(il>hg)il--,T[a[il]]++;
mex=last;i++;
}
}
for(int i=1;i<=m;i++)
wr(ans_[i]),putchar('\n');
return 0;
}


