kruskal 及其应用

kruskal

最小生成树

kruskal 是一种常见且好理解的最小生成树（MST）算法。

前置知识

看到路径压缩就可以了。

生成树

在有 n 的顶点的无向图中，取其中 n-1 条边相连，所得到的树即为生成树。

最小生成树就是生成树边权和最小。

kruskal 求 MST

kruskal 基于贪心。

如果让你的选择之和最小，该怎么选？

显然啊，每次选择的边权都是没选过的最小的，直到选了 n-1 条边。

但这样选有时会出问题。

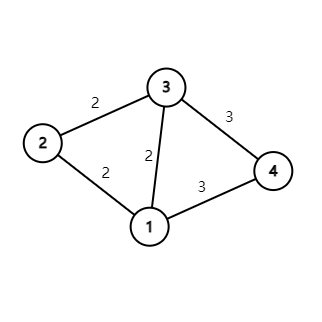
如上图，选最小的边应该是：

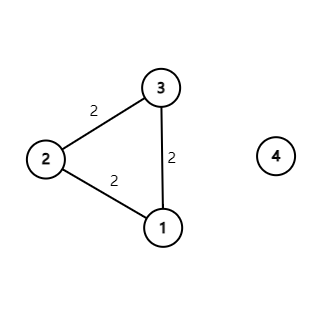
但显然，这不是一个树。

所以在连边之前，还要判断一下两个点是否在同一个连通块内。

判连通用什么？

Link-Cut Tree 并查集！

那么整个 kruskal 的过程就是：

排序 -> 判连通 -> 加边 -> 判连通 -> 加边 -> 判连通 -> 加边……。

Code(P3366)

const int inf=2e5+7;
int n,m,mst,cnt;
int fa[inf];
struct edge{
	int s,t,k;
	bool operator <(const edge &b)const
	{
		return k<b.k;
	}
}h[inf];
int find(int x){return (fa[x]^x)?(fa[x]=find(fa[x])):x;}
int main()
{
	n=re();m=re();
	for(int i=1;i<=n;i++)fa[i]=i;
	for(int i=1;i<=m;i++)
		h[i].s=re(),h[i].t=re(),h[i].k=re();
	sort(h+1,h+m+1);//排序
	for(int i=1;i<=m;i++)
	{
		int r1=find(h[i].s),r2=find(h[i].t);
		if(r1==r2)continue;//判连通
		fa[r1]=r2;
		cnt++,mst+=h[i].k;//加边
		if(cnt==n-1)break;
	}
	if(cnt==n-1)wr(mst,'\n');
	else puts("orz");
	return 0;
}

练习

P4826

P2212

次小生成树

前置知识

为方便叙述，最小生成树中的 \(n-1\) 边叫做树边，剩余的 \(m-n+1\) 条边叫非树边。

非严格次小生成树

显然，对于已经生成的最小生成树来说，每一条非树边的加入，都会形成一个环。那么再将环上的树边中最大的边删除，就能得到次小生成树的一颗候选树。

令最小生成树大小为 \(minn\)，新加入的非树边权值为 \(new\)，环上的最大树边为 \(max\)，那么候选树的大小就是 \(minn-max+new\)，我们所求则是 \(min\{minn-max+new\}\)。

严格次小生成树

当 \(new=max\) 时，若按上述方法进行维护，得到的 \((minn-max+new)=minn\)。

此时，就应该选择环上树边的次大值 \(nexm\)，\((minn-nexm+new)>minn\)。

解法

现在的问题就在于，如何快速求出两点间树边的最大值和次大值。

若直接用两个二维数组将两点间的最大值，次大值存下来是不现实的，\(O(n^2)\) 的空间复杂度不允许。

考虑倍增，储存下来每个节点到其 \(2^j\) 级祖先的最大值（严格时还需要统计次大值），然后在跳 lca 的过程中维护路径上可以加入候选树的最大值。

时间复杂度 \(O(m\log n)\)。

const int inf=3e5+7;
int n,m,mst,ans=1e18;
int fa[inf];
struct kruskal{
	int s,t,v;
	bool operator <(const kruskal &b)const
	{
		return v<b.v;
	}
}h[inf];
int fir[inf],nex[inf<<1],poi[inf<<1],val[inf<<1],sum;
void ins(int x,int y,int z)
{
	nex[++sum]=fir[x];
	poi[sum]=y;
	val[sum]=z;
	fir[x]=sum;
}
bool vis[inf];int cnt;
int find(int s)
{
	if(s==fa[s])return s;
	return fa[s]=find(fa[s]);
}
int dep[inf],fat[inf][20];
int maxn[inf][20],nexm[inf][20];
void dfs(int now,int from)
{
	fat[now][0]=from;
	dep[now]=dep[from]+1;
	for(int i=fir[now];i;i=nex[i])
	{
		int p=poi[i];
		if(p==from)continue;
		maxn[p][0]=val[i];
		dfs(p,now);
	}
}
int pd(int x,int i,int z)
{//判断是否与新加入的非树边相等
	return (maxn[x][i]^z)?maxn[x][i]:nexm[x][i];
}
int ask(int x,int y,int z)
{//倍增 lca 维护最大、次大值
	int max_=-2147483647;
	if(dep[x]<dep[y])swap(x,y);
	for(int i=19;i>=0;i--)
	{
		if(dep[fat[x][i]]>=dep[y])
		{
			max_=max(max_,pd(x,i,z));
			x=fat[x][i];
		}
	}
	if(x==y)return max_;
	for(int i=19;i>=0;i--)
	{
		if(fat[x][i]^fat[y][i])
		{
			max_=max(max_,max(pd(x,i,z),pd(y,i,z)));
			x=fat[x][i],y=fat[y][i];
		}
	}
	return max(max_,max(pd(x,0,z),pd(y,0,z)));
}
signed main()
{
	n=re();m=re();
	for(int i=1;i<=n;i++)fa[i]=i;
	for(int i=1;i<=m;i++)
		h[i].s=re(),h[i].t=re(),h[i].v=re();
	sort(h+1,h+m+1);
	for(int i=1;i<=m;i++)
	{//最小生成树
		int r1=find(h[i].s),r2=find(h[i].t);
		if(r1==r2)continue;
		cnt++;mst+=h[i].v;
		fa[r1]=r2;vis[i]=1;
		ins(h[i].s,h[i].t,h[i].v);
		ins(h[i].t,h[i].s,h[i].v);
		if(cnt==n-1)break;
	}
	for(int i=1;i<=n;i++)//赋初值
		for(int j=0;j<20;j++)
			maxn[i][j]=nexm[i][j]=-2147483647;
	dfs(1,1);
	for(int j=1;j<20;j++)
	{//倍增的预处理
		for(int i=1;i<=n;i++)
		{
			int f=fat[i][j-1];fat[i][j]=fat[f][j-1];
			maxn[i][j]=max(maxn[i][j-1],maxn[f][j-1]);
			if(maxn[i][j-1]==maxn[f][j-1])//分类讨论次大值
				nexm[i][j]=max(nexm[i][j-1],nexm[f][j-1]);
			else if(maxn[i][j-1]<maxn[f][j-1])
				nexm[i][j]=max(maxn[i][j-1],nexm[f][j-1]);
			else nexm[i][j]=max(nexm[i][j-1],maxn[f][j-1]);
		}
	}
	for(int i=1;i<=m;i++)
	{
		if(vis[i])continue;
		int max_=ask(h[i].s,h[i].t,h[i].v);
		if(max_^h[i].v)ans=min(ans,mst+h[i].v-max_);
	}
	wr(ans),putchar('\n');
	return 0;
}

kruskal 重构树

用途

巧妙地求解询问连接两点的所有路径中最大边的最小值或者最小边的最大值问题。

思路

kruskal 求 MST 的时候是逐步加边，而 kruskal 重构树则是将要加的边转化成点，并连接原来的两个点，边权为点权。

就像这样：

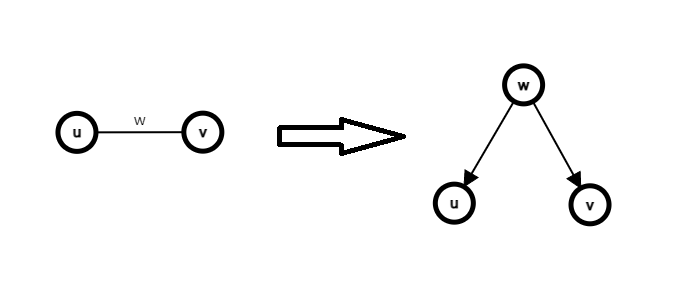
实例（图片来自 OI-Wiki）

原无向图：

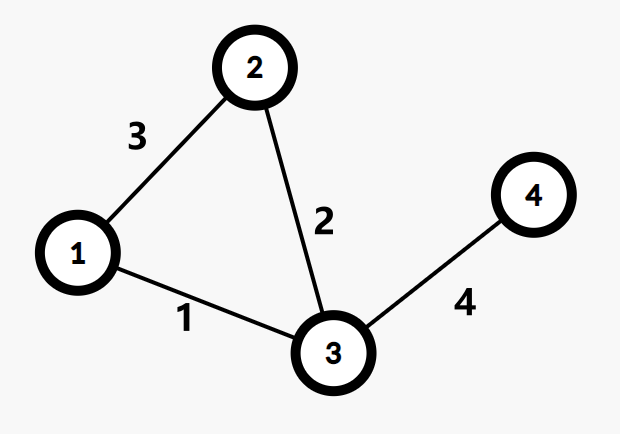
重构树：

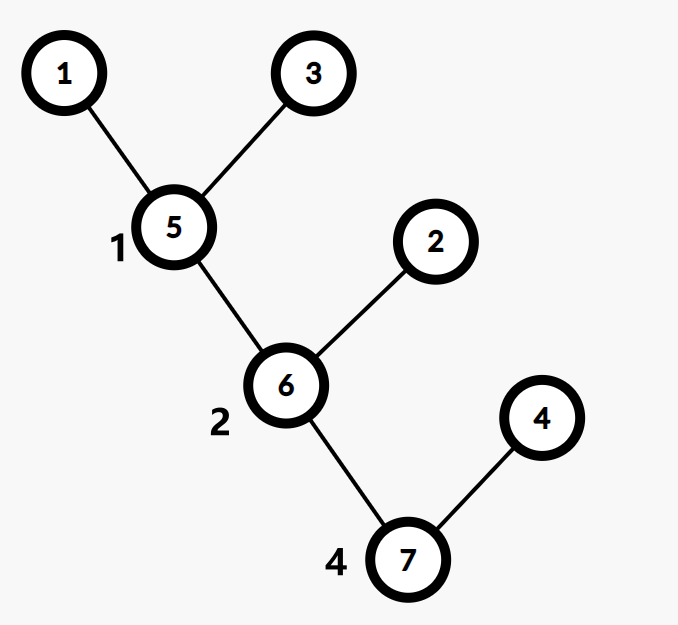
性质

  • kruskal 重构树是一棵二叉堆
  • 最小生成树的重构树是大根堆，最大生成树的重构树是小根堆
  • 图上两点最小路径的最大值或最大路径的最小值为重构树上两点的 lca 的点权。
  • 重构树上共 \(2n-1\) 的点，其中，\(n\) 个叶节点为原来图中的节点。

例题讲解

归程

这个题可以用可持久化并查集切掉。

原谅我不会

海拔比水位高的路车可以通过，剩下的路只能步行涉水。

显然，需要优先走海拔比较高的路径，这样才能尽可能多的行车，也就是先预处理最大生成树。

那么就先预处理出整张图的 kruskal 重构树，然后找到树上的一个节点 v，满足 val[v]>p&&val[fa[v]]<=p，这样，以 x 为根的子树中的叶节点就是能通过车连通的。

提前预处理出图上每个节点到 1 号节点的最短路，然后在重构树中维护每个节点为根时子树中距离 1 号节点的最小值。

至于怎么找到重构树上的节点 x，那就要用到倍增了。

坑点

  1. 最短路用 dijkstra，因为 SPFA 死了。
  2. 多测记得清空，尤其是 lastans 容易忘。

Code

const int inf = 4e5 + 7;
int n, m, q, K, s, lastans;
int fir[inf], nex[inf << 1], poi[inf << 1], val[inf << 1], cnt;
void ins(int x, int y, int z)
{
	nex[++cnt] = fir[x];
	poi[cnt] = y;
	val[cnt] = z;
	fir[x] = cnt;
}
struct node
{
	int id, val;
	node(int id, int val) : id(id), val(val) {}
	bool operator<(const node &b) const
	{
		return val > b.val;
	}
};
int dis[inf];
bool vis[inf];
void dij(int sta)
{
	priority_queue<node> h;
	memset(dis, 127, sizeof(dis));
	memset(vis, 0, sizeof(vis));
	dis[sta] = 0;
	h.push(node(sta, 0));
	while (h.size())
	{
		int now = h.top().id;
		h.pop();
		if (vis[now])
			continue;
		vis[now] = 1;
		for (int i = fir[now]; i; i = nex[i])
		{
			int p = poi[i];
			if (dis[p] > dis[now] + val[i])
			{
				dis[p] = dis[now] + val[i];
				h.push(node(p, dis[p]));
			}
		}
	}
}
struct kru
{
	int f, t, v;
	kru(int f, int t, int v) : f(f), t(t), v(v) {}
	bool operator<(const kru &b) const
	{
		return v > b.v;
	}
};
vector<kru> k;
int ktn;
int fat[inf];
int find(int x)
{
	if (x == fat[x])
		return x;
	return fat[x] = find(fat[x]);
}
struct Kru_Tree
{
	int lc, rc;
	int val, dis;
#define lc(i) T[i].lc
#define rc(i) T[i].rc
} T[inf];
void kruskal()
{
	for (int i = 1; i <= n; i++)
		fat[i] = i;
	sort(k.begin(), k.end());
	for (auto i : k)
	{
		int rf = find(i.f), rt = find(i.t);
		if (rf == rt)
			continue;
		T[++ktn].val = i.v;
		lc(ktn) = rf, rc(ktn) = rt;
		fat[rf] = fat[rt] = fat[ktn] = ktn;
		if (ktn == (2 * n - 1))
			break;
	}
}
int fa[inf][20];
void dfs(int now, int from)
{
	fa[now][0] = from;
	if (lc(now) == 0)
	{
		T[now].dis = dis[now];
		return;
	}
	dfs(lc(now), now);
	dfs(rc(now), now);
	T[now].dis = min(T[lc(now)].dis, T[rc(now)].dis);
}
int ask(int v, int p)
{
	for (int i = 19; i >= 0; i--)
		if (T[fa[v][i]].val > p)
			v = fa[v][i];
	return T[v].dis;
}
void init()
{
	lastans = 0, cnt = 0;
	memset(fir, 0, sizeof(fir));
	memset(fa, 0, sizeof(fa));
	memset(T, 0, sizeof(T));
	k.clear();
}
void solve()
{
	init();
	n = re(), m = re();
	ktn = n;
	for (int i = 1; i <= m; i++)
	{
		int u = re(), v = re(), l = re(), a = re();
		ins(u, v, l), ins(v, u, l);
		k.push_back(kru(u, v, a));
	}
	dij(1);
	kruskal();
	dfs(ktn, ktn);
	for (int j = 1; j < 20; j++)
		for (int i = 1; i <= ktn; i++)
			fa[i][j] = fa[fa[i][j - 1]][j - 1];
	q = re(), K = re(), s = re();
	for (int i = 1; i <= q; i++)
	{
		int v0 = re(), p0 = re();
		int v = (v0 + K * lastans - 1) % n + 1;
		int p = (p0 + K * lastans) % (s + 1);
		wr(lastans = ask(v, p), '\n');
	}
}
int main()
{
	int qwq = re();
	while (qwq--)
		solve();
	return 0;
}

练习

P1967

P4197

P4899

kruskal 相关题目

posted @ 2022-04-04 21:42  Zvelig1205  阅读(168)  评论(0)  编辑  收藏  举报