BST 与 Treap
刚学平衡树的时候写的了,感觉写得好烂。而且现在不记得 Treap 了,也不好维护,更不舍得删,就当是我的黑历史吧。
二叉搜索树
定义
二叉查找树(Binary Search Tree),是一棵空树或者是具有下列性质的二叉树:若它的左子树不空,则左子树上所有结点的值均小于它的根结点的值;若它的右子树不空,则右子树上所有结点的值均大于它的根结点的值;它的左、右子树也分别为二叉排序树。
二叉搜索树作为一种经典的数据结构,它既有链表的快速插入与删除操作的特点,又有数组快速查找的优势;所以应用十分广泛,例如在文件系统和数据库系统一般会采用这种数据结构进行高效率的排序与检索操作。
(上述文字来自百度百科)
简单来说,就是 \(val_{lc(i)}<val_{i}<val_{rc(i)}\),其中序遍历单调递增(当然,递减也是可以的)。
比如这个树:
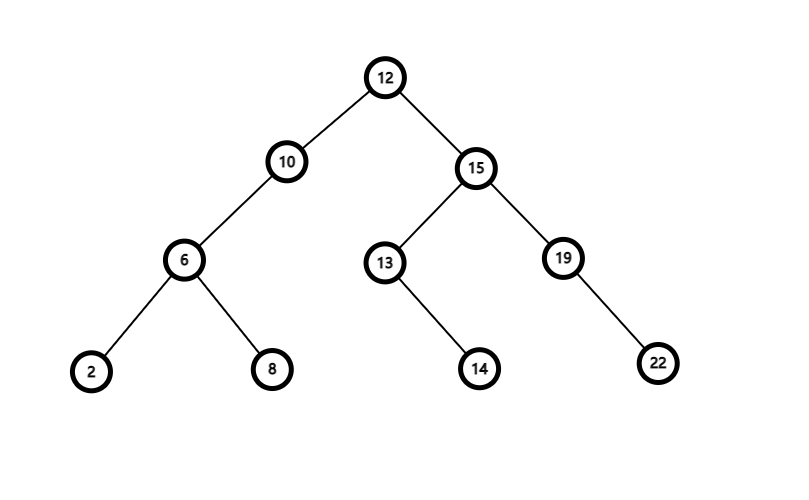
支持操作
- 插入或删除数 k
- 查询数 k 的排名
- 查询 k 小(大)值
- 查询 k 的前驱
- 查询 k 的后继
为方便叙述,本文中的所有相关数据结构均为不可重集。
实现
储存
因为你不知道哪个节点先用,节点会储存什么值,所以会用到动态开点。
众所周知,动态开点有一个特点:认儿子不认爹。
可以看看 这篇博客。
又是二叉树,只需要储存当前节点的值,以当前节点为根的子树大小,左右子节点编号。
像这样:
struct BST{
int val,siz;
int lc,rc;
}T[inf];
void new_node(int &i,int k)
{
i=++cnt;T[i].val=k;T[i].siz=1;
}
子树大小有什么用?别急,下边有。
insert
只需要将插入的值和当前节点的值比较,小左大右,使其满足 BST 性质。
void insert(int &i,int k)
{
if(i==0){new_node(i,k);return;}
T[i].siz++;
if(T[i].val==k)return;
if(k>T[i].val)insert(T[i].rc,k);
else insert(T[i].lc,k);
}
remove
BST 的删除比较麻烦,一般不讨论。
ask_rnk
同样依据 BST 性质,如果查找的值比当前节点的值小,就查找左子树;否则查询右子树,再加上左子树 siz+1。
int ask_rnk(int i,int key)
{
if(i==0)return 1;
if(key<T[i].val)return ask_rnk(T[i].lc,key);
else return ask_rnk(T[i].rc,key)+T[T[i].lc].siz+1;
}
这 siz 不就用上了嘛。
ask_kth
如果左子树 siz 比 k 大,就查询左子树;如果左子树 siz+1=k,说明当前节点就是 kth;否则查询右子树的 k- 左子树 siz-1。
int ask_kth(int i,int key)
{
if(T[T[i].lc].siz+1==key)return T[i].val;
if(key<T[T[i].lc].siz)return ask_kth(T[i].lc,key);
else return ask_kth(T[i].rc,key-T[T[i].lc].siz-1);
}
ask_pre
前驱:小于中最大的。
向右走说明当前节点小,可能是前驱;向右走说明比当前节点大,不可能是前驱。
可能是前驱的中最大的即为前驱。
int ask_pre(int i,int key)
{
if(i==0)return -2147483647;
if(T[i].val>key)return ask_pre(T[i].lc,key);
else return max(T[i].val,ask_pre(T[i].rc,key));
}
ask_nex
后继:大于中最小的。
和前驱差不多,只是左右相反,且求最小。
int ask_nex(int i,int key)
{
if(i==0)return 2147483647;
if(T[i].val>key)return ask_nex(T[i].rc,key);
else return min(T[i].val,ask_nex(T[i].lc,key));
}
复杂度分析
期望复杂度:\(O(n\log n)\)。
最差复杂度:\(O(n^2)\)。
因为如果插入的序列是单调的,会使我们的 BST 退化成一条链,单次复杂度 \(O(n)\),因此需要平衡操作。
Treap
Treap=Tree+Heap
Tree 指的就是上述 BST,而 Heap 指堆。
所以 Treap 的中文翻译就是树堆。
堆
堆,一种完全二叉树。这不就避免退化成链了吗
堆有大根堆和小根堆,不过由于 STL 的原因,C++ 中很少有人手打堆,而是直接用 priority_queue,这就导致了有些人只知道堆,但不了解它的工作原理。
priority_queue 支持的操作有:插入(push),查询最值(top),弹出最值(pop)。堆还支持删除任意数(remove),不过不常用。
堆的主要操作有两个:上浮 和 下沉。具体实现方式,前两篇题解讲的还是挺好的。
rotate
从性质来看,树和堆是两个矛盾的数据结构。
不过,我们引入堆是利用它是一个完全二叉树来防止退化成链,所以整棵树还是一棵 BST。
所以我们给 Treap 的每个节点赋上随机值 heap,让 val 满足 BST 性质,heap 满足堆性质。
就像这样(图片来源于 洛谷日报)

所以要如何在插入节点后使 heap 满足堆性质呢?
旋转(rotation)。
那么,如何旋转呢?
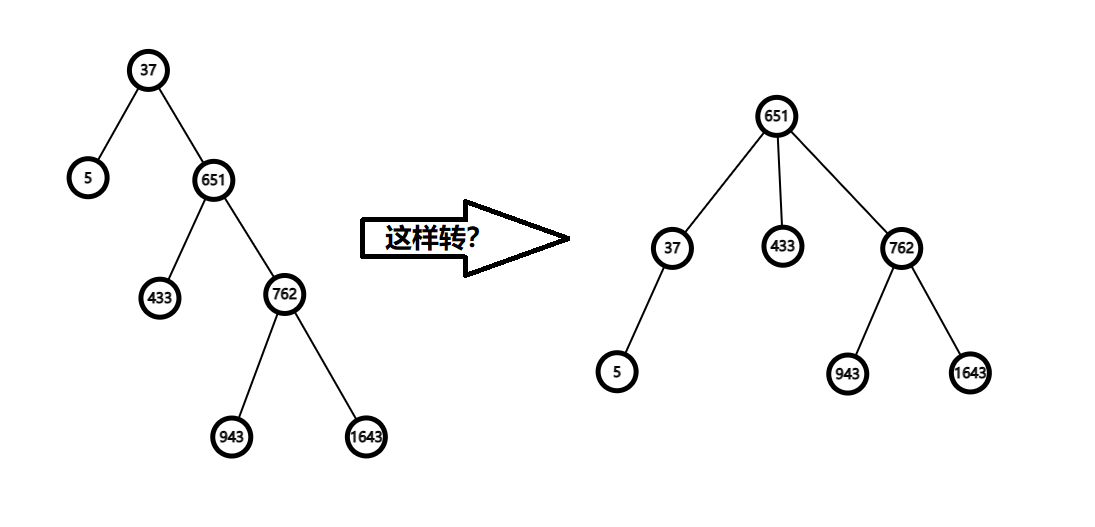
显然,这样是不行的,因为 651 变成三叉了……
但经过观察可以发现,原来 37 既有左儿子又有右儿子,但这样旋转之后,就只剩下左儿子了。而且,433 若成为 37 的的右儿子并不破坏 Treap 的 BST 性质。
所以应该这样转:

这是巧合吗?
看一下一般情况:

按上述转法,转完之后就是:
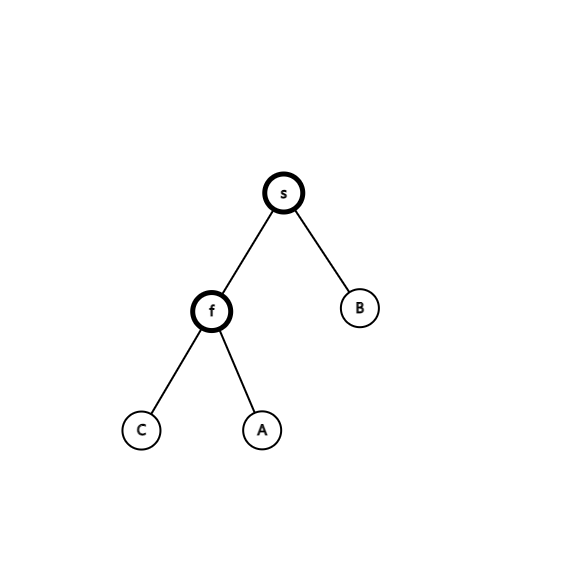
(小写字母表示节点,大写字母表示子树)
对于上边的图的中序遍历是 CfAsB,下边的图中序遍历也是 CfAsB,可见旋转并没有破坏 BST 性质。
所以这样转是正确的,这就是左旋。
有左旋,就有右旋。就像这样:

左旋 f= 右旋 s
再以左旋为例,看一下相对关系:
- s 是 f 的右儿子
- f 的左儿子不变;
- s 的右儿子不变;
- f 的右儿子变为 s 的左儿子;
- s 的左儿子变为 f;
那么代码就是这样的:
void pushup(int i)
{
T[i].siz=T[T[i].lc].siz+T[T[i].rc].siz+1;
}
void zig(int &i)//左旋
{
int s=T[i].rc;
T[i].rc=T[s].lc;
T[s].lc=i;
pushup(i);pushup(s);
i=s;
}
void zag(int &i)//右旋
{
int s=T[i].lc;
T[i].lc=T[s].rc;
T[s].rc=i;
pushup(i);pushup(s);
i=s;
}
当然,用 \(son_0\) 表示左儿子,\(son_1\) 表示右儿子,旋转操作还可以合并成:
void pushup(int i)
{
T[i].siz=T[T[i].lc].siz+T[T[i].rc].siz+1;
}
void rotate(int &i,int t)
{
int s=T[i].son[t^1];
T[i].son[t^1]=T[s].son[t];
T[s].son[t]=i;
pushup(i);pushup(s);
i=s;
}
其他操作
了解如何旋转之后,那么什么时候进行旋转操作呢?
在插入节点的时候,节点根据 BST 性质找到合适的位置;插入完成后,再比较当前节点和左右子节点的 heap,不满足堆性质的就旋转。
此处的堆性质可以是大根堆,也可以是小根堆。
void insert(int &i,int key)
{
if(i==0)
{
i=++cnt;T[i].heap=rand();
T[i].siz=1;T[i].val=key;
return;
}
T[i].siz++;
if(key>T[i].val)
{
insert(T[i].rc,key);
if(T[T[i].rc].heap<T[i].heap)
zig(i);
}
else
{
insert(T[i].lc,key);
if(T[T[i].lc].heap<T[i].heap)
zag(i);
}
}
之前说过,BST 的删除比较麻烦,相比之下,堆的删除就简单了许多。
将我们要删除的节点转到叶节点的位置,然后再删除。
删除的时候也要考虑堆性质,和插入时保持一致。
void remove(int &i,int key)
{
if(T[i].val==key)
{
if(T[i].lc==0||T[i].rc==0)
{
i=T[i].lc+T[i].rc;
return;
}
if(T[T[i].lc].heap<T[T[i].rc].heap)
zig(i),remove(T[i].lc,key);
else zag(i),remove(T[i].rc,key);
}
else if(key<T[i].val)
remove(T[i].lc,key);
else remove(T[i].rc,key);
pushup(i);
}
4 个查询操作和 BST 的查询完全相同(本来堆就是打辅助的)。
Code
const int inf=1e5+7;
int n,root,op,x,cnt;
struct Treap{
int val,heap;
int siz,son[2];
#define lc(i) T[i].son[0]
#define rc(i) T[i].son[1]
}T[inf];
int max(int a,int b){return a>b?a:b;}
int min(int a,int b){return a<b?a:b;}
void pushup(int i)
{
T[i].siz=T[lc(i)].siz+T[rc(i)].siz+1;
}
void rotate(int &i,int t)
{
int s=T[i].son[t^1];
T[i].son[t^1]=T[s].son[t];
T[s].son[t]=i;
pushup(i);pushup(s);
i=s;
}
void new_node(int &i,int k)
{
i=++cnt;
T[i].val=k;
T[i].siz=1;
T[i].heap=rand();
}
void insert(int &i,int k)
{
if(i==0){new_node(i,k);return;}
T[i].siz++;
if(k>T[i].val)
{
insert(rc(i),k);
if(T[rc(i)].heap<T[i].heap)
rotate(i,0);
}
else
{
insert(lc(i),k);
if(T[lc(i)].heap<T[i].heap)
rotate(i,1);
}
}
void remove(int &i,int k)
{
if(T[i].val==k)
{
if(lc(i)==0||rc(i)==0)
{
i=lc(i)+rc(i);
return;
}
if(T[lc(i)].heap<T[rc(i)].heap)
rotate(i,0),remove(lc(i),k);
else rotate(i,1),remove(rc(i),k);
}
else if(k<T[i].val)
remove(lc(i),k);
else remove(rc(i),k);
pushup(i);
}
int ask_rnk(int i,int k)
{
if(i==0)return 1;
if(k<=T[i].val)return ask_rnk(lc(i),k);
return ask_rnk(rc(i),k)+T[lc(i)].siz+1;
}
int ask_kth(int i,int k)
{
if(T[lc(i)].siz+1==k)return T[i].val;
if(k<=T[lc(i)].siz)return ask_kth(lc(i),k);
return ask_kth(rc(i),k-T[lc(i)].siz-1);
}
int ask_pre(int i,int k)
{
if(i==0)return -2147483647;
if(T[i].val>=k)return ask_pre(lc(i),k);
return max(T[i].val,ask_pre(rc(i),k));
}
int ask_nex(int i,int k)
{
if(i==0)return 2147483647;
if(T[i].val<=k)return ask_nex(rc(i),k);
return min(T[i].val,ask_nex(lc(i),k));
}
int main()
{
n=re();
for(int i=1;i<=n;i++)
{
op=re();x=re();
if(op==1)insert(root,x);
if(op==2)remove(root,x);
if(op==3)wr(ask_rnk(root,x));
if(op==4)wr(ask_kth(root,x));
if(op==5)wr(ask_pre(root,x));
if(op==6)wr(ask_nex(root,x));
}
return 0;
}
复杂度分析
回到最初的 BST,BST 退化的原因是什么呢?
顺序插入单调序列。
如果 heap 不随机,而是元素下标,那么顺序插入单调序列还是形成一条链。
不过因为 heap 值是随机的,就相当于将单调序列随机打乱后插入 BST,所以 Treap 的期望高度是 \(O(\log n)\),每次操作的期望复杂度为 \(O(\log n)\)。

图片来自 洛谷博客,侵权紫衫。
Splay 和 Fhq_Treap
自己写的。
替罪羊树
自己写的。
AVL 树
理解,没码过。
红黑树
不会。


