树链剖分之重链剖分
树链剖分
将树转化为线性序列,便于维护树上信息。
include: 重链剖分,长链剖分,实链剖分。
注:此文默认读者已经熟悉线段树的基本操作,不熟悉这可以先看这个:线段树
重链剖分
剖树
-
建图
很普通的邻接表存图:
void ins(int x,int y)
{
nex[++cnt]=fir[x];
poi[cnt]=y;
fir[x]=cnt;
}
-
通过第一遍
dfs,统计出每个节点的:-
父节点
fa; -
深度
dep; -
以当前节点为根的子树大小
siz; -
当前节点所有子节点对应的子树中 siz 最大的节点,即重儿子
son;
-
int fa[inf],son[inf],siz[inf],dep[inf];
void dfs1(int now,int from)
{
fa[now]=from;siz[now]=1;
dep[now]=dep[from]+1;
for(int i=fir[now];i;i=nex[i])
{
int p=poi[i];
if(p==from)continue;
dfs1(p,now);
siz[now]+=siz[p];
if(siz[son[now]]<siz[p])
son[now]=p;
}
}
-
然后用第二遍
dfs,统计出:-
每条链的顶点
top; -
节点的时间戳
dfn; -
时间戳所对应的节点
rnk,即rnk[dfn[x]]=x。
第二次
dfs中,在确保深度优先的前提下,以重儿子优先搜索,以确保每条重链的时间戳是连续的。 -
int top[inf],dfn[inf],rnk[inf],sum;
void dfs2(int now,int topn)
{
top[now]=topn;
dfn[now]=++sum;rnk[sum]=now;
if(!son[now])return;
dfs2(son[now],topn);
for(int i=fir[now];i;i=nex[i])
{
int p=poi[i];
if(dfn[p])continue;
dfs2(p,p);
}
}
- 效果展示
经过两次 dfs,就将一棵树上的点按照 dfn 映射到了一个线性的序列上了。
如下边这棵树:
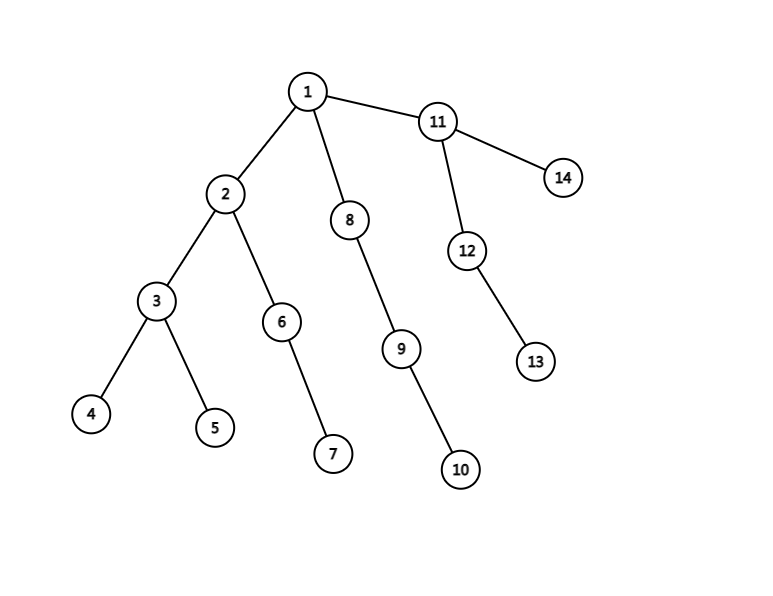
两次 dfs 之后这个树就是:
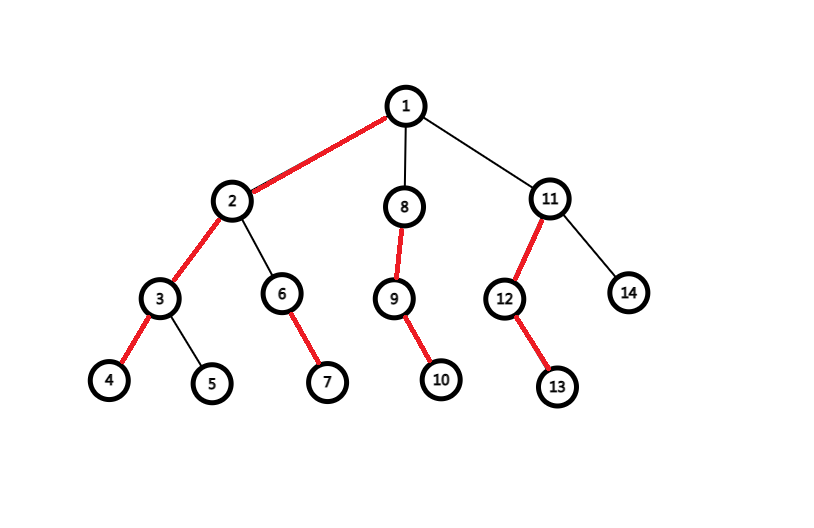
点中的数表示 dfs 序;红色的边表示重链,黑色的边表示轻链。
映射到线性序列,然后就可以用各种各样的数据结构(如线段树,分块,珂朵莉树,甚至直接暴力)来维护这个序列了。
luogu 模板
题目中包括 4 个操作:
-
1 x y z表示将树上从 \(x\) 到 \(y\) 节点的最短路径上的节点权值都加上 \(z\)。 -
2 x y表示查询树上从 \(x\) 到 \(y\) 节点的最短路径上的节点权值之和。 -
3 x z表示将树上以 \(x\) 为根的子树上所有节点的权值都加上 \(z\)。 -
4 x表示查询树上以 \(x\) 为根的子树上所有节点的权值之和。
可以分为两种:维护子树和维护链。
- 维护子树
观察上图,可以发现,同一子树上的点的 dfn 是连续的。也就是说,同一子树上的点在序列上也是连续的。举个例子:以 11 为根的子树的 siz 是 4,子树对应的 dfn 是从 11 到 14(即 11+4-1)。那么便可以直接进行区间维护。
void update(int i,int l,int r,int k)
{
if(l<=T[i].le&&T[i].ri<=r)
{
T[i].val+=(T[i].ri-T[i].le+1)*k;T[i].val%=mod;
T[i].tag+=k;T[i].tag%=mod;
return;
}
if(T[i].tag)pushdown(i);
int mid=(T[i].le+T[i].ri)>>1;
if(l<=mid)update(i<<1,l,r,k);
if(mid<r)update(i<<1|1,l,r,k);
T[i].val=(T[i<<1].val+T[i<<1|1].val)%mod;
}
int ask(int i,int l,int r)
{
if(l<=T[i].le&&T[i].ri<=r)
return T[i].val%mod;
if(T[i].tag)pushdown(i);
int mid=(T[i].le+T[i].ri)>>1,ans=0;
if(l<=mid)ans+=ask(i<<1,l,r),ans%=mod;
if(mid<r)ans+=ask(i<<1|1,l,r),ans%=mod;
return ans%mod;
}
- 维护链
在树上两点的简单路径必然经过 lca,而重链的时间戳是连续的。
那么可以在跳 lca 的过程中维护经过的重链。
void chain_add(int x,int y,int k)
{
while(top[x]!=top[y])
{
if(dep[top[x]]<dep[top[y]])x^=y^=x^=y;
update(1,dfn[top[x]],dfn[x],k);
x=fa[top[x]];
}
if(dep[x]>dep[y])x^=y^=x^=y;
update(1,dfn[x],dfn[y],k);
}
int chain_ask(int x,int y)
{
int ans=0;
while(top[x]!=top[y])
{
if(dep[top[x]]<dep[top[y]])x^=y^=x^=y;
ans+=ask(1,dfn[top[x]],dfn[x]);ans%=mod;
x=fa[top[x]];
}
if(dep[x]>dep[y])x^=y^=x^=y;
ans+=ask(1,dfn[x],dfn[y]);
return ans%mod;
}
完整代码
cosnt int inf=1e5+7;
struct Seg_Tree{
int le,ri;
int tag,val;
}T[inf<<2];
int n,m,root,mod,op,x,y,k,a[inf];
int fir[inf],nex[inf<<1],poi[inf<<1],cnt;
void ins(int x,int y)
{
nex[++cnt]=fir[x];
poi[cnt]=y;
fir[x]=cnt;
}
int fa[inf],son[inf],siz[inf],dep[inf];
void dfs1(int now,int from)
{
fa[now]=from;siz[now]=1;
dep[now]=dep[from]+1;
int maxn=0;
for(int i=fir[now];i;i=nex[i])
{
int p=poi[i];
if(p==from)continue;
dfs1(p,now);
siz[now]+=siz[p];
if(siz[son[now]]<siz[p])
son[now]=p;
}
}
int top[inf],dfn[inf],rnk[inf],sum;
void dfs2(int now,int topn)
{
top[now]=topn;
dfn[now]=++sum;rnk[sum]=now;
if(!son[now])return;
dfs2(son[now],topn);
for(int i=fir[now];i;i=nex[i])
{
int p=poi[i];
if(dfn[p])continue;
dfs2(p,p);
}
}
void build(int i,int l,int r)
{
T[i].le=l;T[i].ri=r;
if(l==r)
{
T[i].val=a[rnk[l]]%mod;
return;
}
int mid=(l+r)>>1;
build(i<<1,l,mid);
build(i<<1|1,mid+1,r);
T[i].val=(T[i<<1].val+T[i<<1|1].val)%mod;
}
void pushdown(int i)
{
T[i<<1].val+=(T[i<<1].ri-T[i<<1].le+1)*T[i].tag;
T[i<<1|1].val+=(T[i<<1|1].ri-T[i<<1|1].le+1)*T[i].tag;
T[i<<1].val%=mod;T[i<<1|1].val%=mod;
T[i<<1].tag+=T[i].tag;T[i<<1].tag%=mod;
T[i<<1|1].tag+=T[i].tag;T[i<<1|1].tag%=mod;
T[i].tag=0;
}
void update(int i,int l,int r,int k)
{
if(l<=T[i].le&&T[i].ri<=r)
{
T[i].val+=(T[i].ri-T[i].le+1)*k;T[i].val%=mod;
T[i].tag+=k;T[i].tag%=mod;
return;
}
if(T[i].tag)pushdown(i);
int mid=(T[i].le+T[i].ri)>>1;
if(l<=mid)update(i<<1,l,r,k);
if(mid<r)update(i<<1|1,l,r,k);
T[i].val=(T[i<<1].val+T[i<<1|1].val)%mod;
}
int ask(int i,int l,int r)
{
if(l<=T[i].le&&T[i].ri<=r)
return T[i].val%mod;
if(T[i].tag)pushdown(i);
int mid=(T[i].le+T[i].ri)>>1,ans=0;
if(l<=mid)ans+=ask(i<<1,l,r),ans%=mod;
if(mid<r)ans+=ask(i<<1|1,l,r),ans%=mod;
return ans%mod;
}
void chain_add(int x,int y,int k)
{
while(top[x]!=top[y])
{
if(dep[top[x]]<dep[top[y]])x^=y^=x^=y;
update(1,dfn[top[x]],dfn[x],k);
x=fa[top[x]];
}
if(dep[x]>dep[y])x^=y^=x^=y;
update(1,dfn[x],dfn[y],k);
}
int chain_ask(int x,int y)
{
int ans=0;
while(top[x]!=top[y])
{
if(dep[top[x]]<dep[top[y]])x^=y^=x^=y;
ans+=ask(1,dfn[top[x]],dfn[x]);ans%=mod;
x=fa[top[x]];
}
if(dep[x]>dep[y])x^=y^=x^=y;
ans+=ask(1,dfn[x],dfn[y]);
return ans%mod;
}
signed main()
{
n=re();m=re();root=re();mod=re();
for(int i=1;i<=n;i++)
a[i]=re();
for(int i=1;i<n;i++)
{
int u=re(),v=re();
ins(u,v);ins(v,u);
}
dfs1(root,root);
dfs2(root,root);
build(1,1,n);
for(int i=1;i<=m;i++)
{
op=re();x=re();
if(op==1)y=re(),k=re(),chain_add(x,y,k%mod);
if(op==2)y=re(),wr(chain_ask(x,y)%mod),putchar('\n');
if(op==3)k=re(),update(1,dfn[x],dfn[x]+siz[x]-1,k%mod);
if(op==4)wr(ask(1,dfn[x],dfn[x]+siz[x]-1)%mod),putchar('\n');
}
return 0;
}
时间复杂度
树剖有两条性质:
- 如果 \((x,y)\) 是轻链,那么必有 \(2\cdot siz_y<siz_x\)
- 根节点到任意节点的路径上的轻重链个数都少于 \(\log n\)
综上,树剖的时间复杂度就是 \(O(n\log n)\) 的。
再套上线段树,时间复杂度为 \(O(n\log^2n)\)。
当然,树剖不一定要结合线段树,或者说不一定要结合数据结构。因为树剖之后有一些美妙的性质,可以以此维护一些树上信息。
例题选讲
树剖维护树上信息
第一篇题解我写的
树剖珂朵莉树
话说我珂朵莉比分块学得早
题意转化为树剖问题就是:
- 子树推平为 0
- 链上推平为 1
区间推平,那必然是珂朵莉啊。
不过,这个题不开 O2 会 T 掉,不知道当年考场上开了吗。
const int inf=1e5+7;
int n,m,x;
struct Chtholly{
int l,r;
mutable int val;
Chtholly(int l,int r,int val):
l(l),r(r),val(val){}
bool operator <(const Chtholly &b)const
{
return l<b.l;
}
};
set<Chtholly>tre;
#define IT set<Chtholly>::iterator
int fir[inf],nex[inf],poi[inf],cnt;
void ins(int x,int y)
{
nex[++cnt]=fir[x];
poi[cnt]=y;
fir[x]=cnt;
}
int fa[inf],dep[inf],siz[inf],son[inf];
void dfs1(int now,int from)
{
siz[now]=1;fa[now]=from;
dep[now]=dep[from]+1;
for(int i=fir[now];i;i=nex[i])
{
int p=poi[i];
if(p==from)continue;
dfs1(p,now);
siz[now]+=siz[p];
if(siz[son[now]]<siz[p])
son[now]=p;
}
}
int top[inf],dfn[inf],rnk[inf],sum;
void dfs2(int now,int topn)
{
top[now]=topn;
dfn[now]=++sum;rnk[sum]=now;
if(son[now]==0)return;
dfs2(son[now],topn);
for(int i=fir[now];i;i=nex[i])
{
int p=poi[i];
if(dfn[p])continue;
dfs2(p,p);
}
}
IT split(int now)
{
IT i=tre.lower_bound(Chtholly(now,0,0));
if(i!=tre.end()&&i->l==now)return i;
i--;int l=i->l,r=i->r,v=i->val;
tre.erase(i);
tre.insert(Chtholly(l,now-1,v));
return tre.insert(Chtholly(now,r,v)).first;
}
int assign(int l,int r,int k)
{
IT ir=split(r+1),il=split(l),i=il;
int ans=0;
while(i!=ir)
{
if(i->val!=k)ans+=i->r-i->l+1;
i++;
}
tre.erase(il,ir);
tre.insert(Chtholly(l,r,k));
return ans;
}
int cover(int l,int r,int k)
{
int ans=0;
while(top[l]!=top[r])
{
ans+=assign(dfn[top[r]],dfn[r],k);
r=fa[top[r]];
}
ans+=assign(dfn[l],dfn[r],k);
return ans;
}
int main()
{
n=re();
for(int i=1;i<n;i++)
ins(re()+1,i+1);
dfs1(1,1);dfs2(1,1);
tre.insert(Chtholly(1,n,0));
m=re();
for(int i=1;i<=m;i++)
{
char s[10]="";
scanf("%s",s);x=re()+1;
if(s[0]=='i')wr(cover(1,x,1)),putchar('\n');
else wr(assign(dfn[x],dfn[x]+siz[x]-1,0)),putchar('\n');
}
return 0;
}
树剖分块
每次单点修改后暴力维护块内的 sum 和 maxn,然后树剖查询。
时间复杂度 \(O(n\sqrt n\log n)\),跑到了最优解第 7。
const int inf=1e5+7;
int n,m,len,a[inf],c[inf];
int fir[inf],nex[inf<<1],poi[inf<<1],cnt;
void ins(int x,int y)
{
nex[++cnt]=fir[x];
poi[cnt]=y;
fir[x]=cnt;
}
int fa[inf],son[inf],siz[inf],dep[inf];
void dfs1(int now,int from)
{
dep[now]=dep[from]+1;
siz[now]=1;fa[now]=from;
for(int i=fir[now];i;i=nex[i])
{
int p=poi[i];
if(p==from)continue;
dfs1(p,now);
siz[now]+=siz[p];
if(siz[son[now]]<siz[p])
son[now]=p;
}
}
int top[inf],dfn[inf],val[inf],col[inf],dfn_;
void dfs2(int now,int topn)
{
top[now]=topn;dfn[now]=++dfn_;
val[dfn_]=a[now];col[dfn_]=c[now];
if(!son[now])return;
dfs2(son[now],topn);
for(int i=fir[now];i;i=nex[i])
{
int p=poi[i];
if(dfn[p])continue;
dfs2(p,p);
}
}
int bel[inf],L[400],R[400];
int sum[inf][400],maxn[inf][400];
int query_sum(int l,int r,int c)
{
int lin=bel[l],rin=bel[r];
int ans=0;
if(lin==rin)
{
for(int i=l;i<=r;i++)
if(col[i]==c)ans+=val[i];
return ans;
}
for(int i=l;i<=R[lin];i++)
if(col[i]==c)ans+=val[i];
for(int i=L[rin];i<=r;i++)
if(col[i]==c)ans+=val[i];
for(int i=lin+1;i<rin;i++)
ans+=sum[c][i];
return ans;
}
int ask_sum(int x,int y,int c)
{
int ans=0;
while(top[x]^top[y])
{
if(dep[top[x]]<dep[top[y]])swap(x,y);
ans+=query_sum(dfn[top[x]],dfn[x],c);
x=fa[top[x]];
}
if(dep[x]>dep[y])swap(x,y);
return ans+query_sum(dfn[x],dfn[y],c);
}
int query_max(int l,int r,int c)
{
int lin=bel[l],rin=bel[r];
int ans=0;
if(lin==rin)
{
for(int i=l;i<=r;i++)
if(col[i]==c)ans=max(ans,val[i]);
return ans;
}
for(int i=l;i<=R[lin];i++)
if(col[i]==c)ans=max(ans,val[i]);
for(int i=L[rin];i<=r;i++)
if(col[i]==c)ans=max(ans,val[i]);
for(int i=lin+1;i<rin;i++)
ans=max(ans,maxn[c][i]);
return ans;
}
int ask_max(int x,int y,int c)
{
int ans=0;
while(top[x]^top[y])
{
if(dep[top[x]]<dep[top[y]])swap(x,y);
ans=max(ans,query_max(dfn[top[x]],dfn[x],c));
x=fa[top[x]];
}
if(dep[x]>dep[y])swap(x,y);
return max(ans,query_max(dfn[x],dfn[y],c));
}
int main()
{
n=re();m=re();len=sqrt(n);
for(int i=1;i<=n;i++)
a[i]=re(),c[i]=re();
for(int i=1;i<n;i++)
{
int u=re(),v=re();
ins(u,v),ins(v,u);
}
dfs1(1,1),dfs2(1,1);
for(int i=1;i<=len;i++)
L[i]=R[i-1]+1,R[i]=i*len;
R[len]=n;
for(int i=1;i<=len;i++)
{
for(int j=L[i];j<=R[i];j++)
{
bel[j]=i,sum[col[j]][i]+=val[j];
maxn[col[j]][i]=max(maxn[col[j]][i],val[j]);
}
}
for(int i=1;i<=m;i++)
{
char op[10]="";scanf("%s",op);
int x=re(),y=re();
if(op[1]=='C')
{
x=dfn[x];
for(int i=L[bel[x]];i<=R[bel[x]];i++)
sum[col[i]][bel[x]]=maxn[col[i]][bel[x]]=0;
col[x]=y;
for(int i=L[bel[x]];i<=R[bel[x]];i++)
{
sum[col[i]][bel[x]]+=val[i];
maxn[col[i]][bel[x]]=max(maxn[col[i]][bel[x]],val[i]);
}
}
if(op[1]=='W')
{
x=dfn[x];
for(int i=L[bel[x]];i<=R[bel[x]];i++)
sum[col[i]][bel[x]]=maxn[col[i]][bel[x]]=0;
val[x]=y;
for(int i=L[bel[x]];i<=R[bel[x]];i++)
{
sum[col[i]][bel[x]]+=val[i];
maxn[col[i]][bel[x]]=max(maxn[col[i]][bel[x]],val[i]);
}
}
if(op[1]=='S')wr(ask_sum(x,y,col[dfn[x]])),putchar('\n');
if(op[1]=='M')wr(ask_max(x,y,col[dfn[x]])),putchar('\n');
}
return 0;
}
练习
换根树剖
先看一道 例题。
操作 1 就是换根,而 2 和 3 是树剖的常规操作:链上更新,子树查询。
第一次看到换根树剖的时候,首先想到的思路是将这个树再剖一遍。但显然时间复杂度不允许。
在学树剖时,我们就将子树操作和链上操作分开讨论了。在这里,我们继续传承优良传统。
链上操作
可以发现,链上更新其实和根的位置没有关系。所以链上推平就可以直接用线段树来解决。
void pushdown(int i)
{
T[i<<1].minn=T[i<<1|1].minn=T[i].tag;
T[i<<1].tag=T[i<<1|1].tag=T[i].tag;
T[i].tag=0;
}
void assign(int i,int l,int r,int k)
{
if(l<=T[i].le&&T[i].ri<=r)
{
T[i].minn=k;
T[i].tag=k;
return;
}
if(T[i].tag)pushdown(i);
int mid=(T[i].le+T[i].ri)>>1;
if(l<=mid)assign(i<<1,l,r,k);
if(mid<r)assign(i<<1|1,l,r,k);
T[i].minn=min(T[i<<1].minn,T[i<<1|1].minn);
}
void swap(int &x,int &y){x^=y^=x^=y;}
void update(int x,int y,int k)
{
while(top[x]!=top[y])
{
if(dep[top[x]]<dep[top[y]])swap(x,y);
assign(1,dfn[top[x]],dfn[x],k);
x=fa[top[x]];
}
if(dep[x]>dep[y])swap(x,y);
assign(1,dfn[x],dfn[y],k);
}
子树操作
但子树查询不同。根的位置不同导致两个节点的 lca 不同,子树更不相同。
那怎么办?

我们可以 破罐子破摔 以 1 为根,先剖一遍。
然后记录下来每次要换成的根 root。
对于要查询的点 x,与 root 存在四种位置关系:
- x 就是 root
- root 是 x 的祖先
- x 和 root 无直接血缘
- x 是 root 的祖先
显然,第 1 种情况以 x 为根的子树就是整棵树,所以直接输出全局 min 值。
那么我们试着分析一下这三种情况中以 x 为根的子树长什么样。
1. root 是 x 的祖先
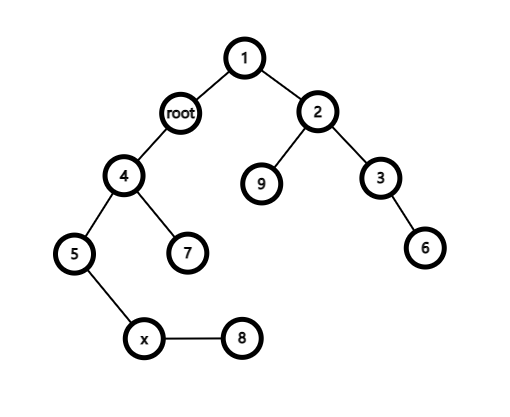
(图丑,凑活看吧)
显然,根为 1 时的 x 子树和根为 root 时的 x 子树没有什么区别,所以直接查询就可以了。
2. root 和 x 无直接血缘
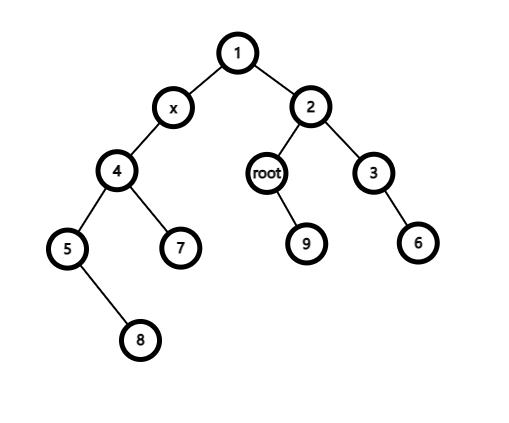
由图可知,此情况和情况 1 相同。
3. x 是 root 的祖先
这种情况就是换根树剖真正需要讨论的了。
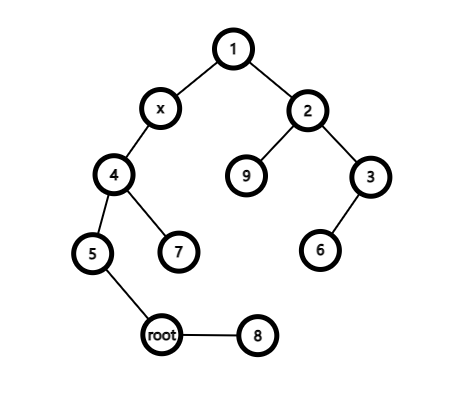
由图,我们先把 root 拉上去:
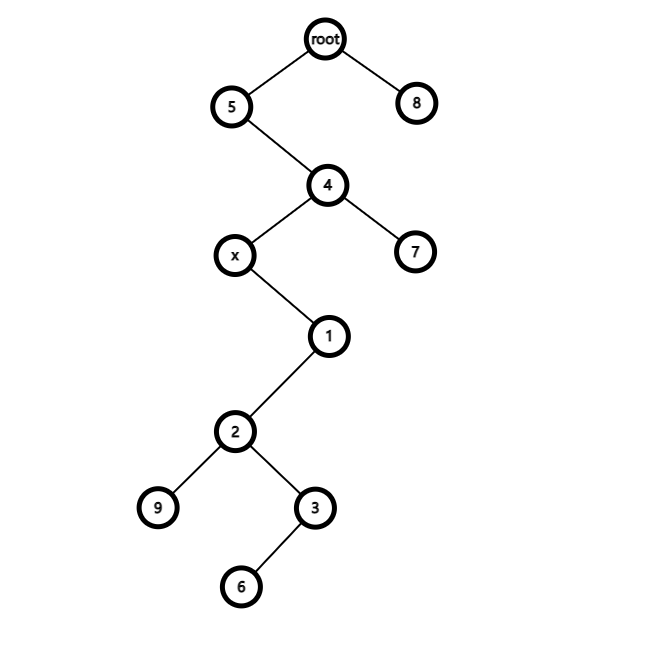
……蜈蚣……
和原图做对比,会发现,除了原图中 x 子树包含 root 的子节点,其余节点均属于新图中以 x 的子树。
那么现在的问题就在于,如何找到这个子树包含 root 的子节点。
暴力跳呗
while(fa[root]!=x)root=fa[root];
确实可以,但……你不是把树剖了吗?
那我们往上跳重链,它不香吗?
如果重链顶点的父亲是 x,就返回重链顶点。
如果 x 已经包含在了重链中,那就返回 x 的重儿子。
否则就向上跳重链。
int find(int x)
{
int now=root;
while(top[now]!=top[x])
{
if(fa[top[now]]==x)return top[now];
now=fa[top[now]];
}
return son[x];
}
那么不查询的是一个子树,时间戳是连续的,查询的就可以拆成两部分:
int ls=find(x);
wr(min(ask(1,1,dfn[ls]-1),ask(1,dfn[ls]+siz[ls],n)));
Code
const int inf=1e5+7;
int n,m,root;
int a[inf];
int fir[inf],nex[inf<<1],poi[inf<<1],cnt;
void ins(int x,int y)
{
nex[++cnt]=fir[x];
poi[cnt]=y;
fir[x]=cnt;
}
int fa[inf],son[inf],dep[inf],siz[inf];
void dfs1(int now,int from)
{
fa[now]=from;siz[now]=1;
dep[now]=dep[from]+1;
for(int i=fir[now];i;i=nex[i])
{
int p=poi[i];
if(p==from)continue;
dfs1(p,now);
siz[now]+=siz[p];
if(siz[p]>siz[son[now]])
son[now]=p;
}
}
int top[inf],dfn[inf],rnk[inf],sum;
void dfs2(int now,int topn)
{
top[now]=topn;
dfn[now]=++sum;rnk[sum]=now;
if(!son[now])return;
dfs2(son[now],topn);
for(int i=fir[now];i;i=nex[i])
{
int p=poi[i];
if(dfn[p])continue;
dfs2(p,p);
}
}
struct Seg_Tree{
int le,ri;
int tag,minn;
}T[inf<<2];
int min(int a,int b){return a<b?a:b;}
void build(int i,int l,int r)
{
T[i].le=l;T[i].ri=r;
if(l==r)
{
T[i].minn=a[rnk[l]];
return;
}
int mid=(l+r)>>1;
build(i<<1,l,mid);
build(i<<1|1,mid+1,r);
T[i].minn=min(T[i<<1].minn,T[i<<1|1].minn);
}
void pushdown(int i)
{
T[i<<1].minn=T[i<<1|1].minn=T[i].tag;
T[i<<1].tag=T[i<<1|1].tag=T[i].tag;
T[i].tag=0;
}
void assign(int i,int l,int r,int k)
{
if(l<=T[i].le&&T[i].ri<=r)
{
T[i].minn=k;
T[i].tag=k;
return;
}
if(T[i].tag)pushdown(i);
int mid=(T[i].le+T[i].ri)>>1;
if(l<=mid)assign(i<<1,l,r,k);
if(mid<r)assign(i<<1|1,l,r,k);
T[i].minn=min(T[i<<1].minn,T[i<<1|1].minn);
}
void swap(int &x,int &y){x^=y^=x^=y;}
void update(int x,int y,int k)
{
while(top[x]!=top[y])
{
if(dep[top[x]]<dep[top[y]])swap(x,y);
assign(1,dfn[top[x]],dfn[x],k);
x=fa[top[x]];
}
if(dep[x]>dep[y])swap(x,y);
assign(1,dfn[x],dfn[y],k);
}
int lca_(int x,int y)
{
while(top[x]!=top[y])
{
if(dep[top[x]]<dep[top[y]])swap(x,y);
x=fa[top[x]];
}
if(dep[x]>dep[y])swap(x,y);
return x;
}
int ask(int i,int l,int r)
{
if(l<=T[i].le&&T[i].ri<=r)
return T[i].minn;
if(T[i].tag)pushdown(i);
int mid=(T[i].le+T[i].ri)>>1,ans=0x7fffffff;
if(l<=mid)ans=min(ans,ask(i<<1,l,r));
if(mid<r)ans=min(ans,ask(i<<1|1,l,r));
return ans;
}
int find(int x)
{
int now=root;
while(top[now]!=top[x])
{
if(fa[top[now]]==x)return top[now];
now=fa[top[now]];
}
return son[x];
}
int main()
{
n=re();m=re();
for(int i=1;i<n;i++)
{
int u=re(),v=re();
ins(u,v),ins(v,u);
}
for(int i=1;i<=n;i++)
a[i]=re();
dfs1(1,1);dfs2(1,1);
root=re();
build(1,1,n);
for(int i=1;i<=m;i++)
{
int op=re();
if(op==1)root=re();
if(op==2)
{
int x=re(),y=re(),k=re();
update(x,y,k);
}
if(op==3)
{
int x=re(),lca=lca_(x,root);
if(x==root)wr(T[1].minn),putchar('\n');
else if(lca==x)
{
int ls=find(x);
wr(min(ask(1,1,dfn[ls]-1),ask(1,dfn[ls]+siz[ls],n)));
putchar('\n');
}
else
{
wr(ask(1,dfn[x],dfn[x]+siz[x]-1));
putchar('\n');
}
}
}
return 0;
}
练习
长链剖分
听说是用来优化 DP 的,鉴于本人 DP 很烂,没有学。
我才不会承认是因为我没学会。。。

