最短路
最短路
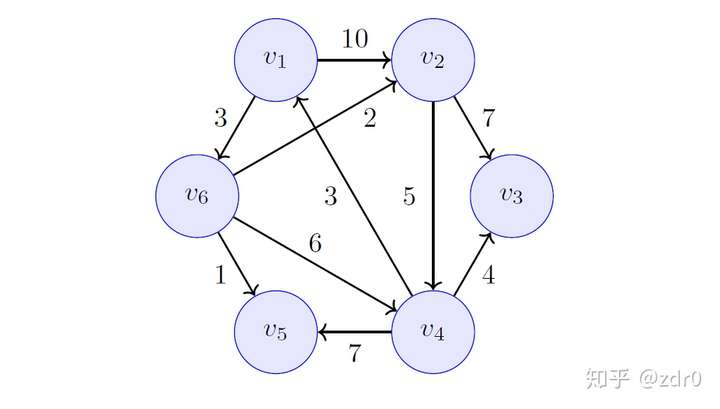
如下图(引自知乎):
求两点之间的最短路径。
最短路有两种:单源和全源。
常用的有四种最短路算法:
- Floyd(全)
- SPFA(单)
- Dijkstra(单)
- Johnson(全)
还有两种最短路的应用:
- 最短路计数
- 最短路径
Floyd(多源最短路)
Floyd 其实是一种 DP 思想。
核心只有四行代码:
for(int k=1;k<=n;k++)
for(int i=1;i<=n;i++)
for(int j=1;j<=n;j++)
v[i][j]=min(v[i][j],v[i][k]+v[k][j]);
v 数组的初始化也非常简单:
\(v_{i,i}=0,v_{i,j}=+\infty\)
再把输入的 i,j 更新就 OK 了
时间复杂度 \(O(n^3)\),空间复杂度 \(O(n^2)\)
需要注意的是一般有人写循环就会直接 for_i_j_k 依次来,但是 Flody 中 k 必须在第一维,否则会 WA 。
比如我们来看一个例子:
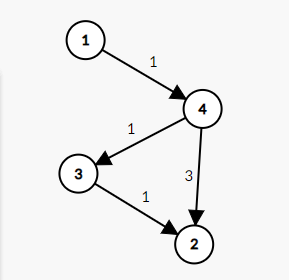
当 \(i=1,j=2,k=3\) 时,此时 \(dis_{1,3}=+\infty\),无法更新到 \(dis_{1,2}\)。
到 \(k=4\) 的时候,将 \(dis_{1,2}\) 更新为 \(dis_{1,4}+dis_{4,3}=4\)。
然后在 \(i=1,j=3,k=4\) 时,更新 \(dis_{1,3}=2\),但无法在将 \(dis_{1,2}\) 更新为 \(dis_{1,3}+dis_{3,2}=3\)。所以在最终结果中, \(dis_{1,2}=4\)。
具体原因就是其思想:DP
用 \(f_{k,i,j}\) 表示经过前 k 的点 i 和 j 的最短路
DP 方程就是 \(f_{k,i,j}=min(f_{k-1,i,j},f_{k-1,i,k}+f_{k-1,k,j})\)
然后滚动数组优化一下,就是 \(f_{i,j}=min(f_{i,j},f_{i,k}+f_{k,j})\)
Floyd 适用于点数较少的图上,可以用来判负环:在经过 Floyd 核心代码处理后的图上再跑一遍 Floyd ,如果有权值被更新,则存在负环。
也可以用来找最小环。
Dijkstra(单源最短路)
Flody 是 DP 的思想,而 Dij 是贪心的思想。
限制条件:无负权。
Dij 的思路主要是:找到每次更新后 dis 值最小的点,用这个最小的点再去维护它所指向的点。
由于没有负边权,所以每次选择最小的点更新的路径一定是最短路。
因为要对图中的 n 的点都进行更新,再加上每次找最小的点又要遍历一次,所有的边还要遍历一遍,所以朴素的 Dij 算法时间复杂度为 \(O(n^2)\) 。
dis[s]=0;
while(!vis[s])
{
int minn=2147483647;
vis[s]=1;
for(int i=fir[s];i;i=nex[i])
{
int p=poi[i];
if(!vis[p]&&dis[p]>dis[s]+val[i])
dis[p]=dis[s]+val[i];
}
for(int i=1;i<=n;i++)
if(!vis[i]&&dis[i]<minn)
minn=dis[i],s=i;
}
在多数情况下我们要对朴素 dij 进行优化。
遍历 n 个点事无法改变的,那么有没有一种办法更快找到最小权值的点?
堆优化
利用二叉小根堆,将点和它的 dis 值存入堆中,每次用 \(O(\log n)\) 的时间取出并删除堆顶,然后遍历其发出的边,更新相邻点的 dis 值。
时间复杂度 \(O(m\log n)\)。
但是 priority_queue 不支持随机删除,所以时间复杂度 \(O(m\log m)\)。
typedef pair<int,int> Pr;
priority_queue<Pr,vector<Pr>,greater<Pr> >h;
memset(dis,127,sizeof(dis));
dis[s]=0;h.push(Pr(0,s));
while(h.size())
{
int now=h.top().second;h.pop();
if(vis[now])continue;
vis[now]=1;
for(int i=fir[now];i;i=nex[i])
{
int p=poi[i];
if(dis[p]>dis[now]+val[i])
{
dis[p]=dis[now]+val[i];
h.push(Pr(dis[p],p));
}
}
}
这里的堆用优先队列来实现,有 STL 就没必要再手打堆。
如果不想用 pair,也可以用 struct 的 operator
struct node{
int id,val;
bool operator <(const node &b)const
{
return val>b.val;
}
};
priority_queue<node>h;
while(h.size())
{
int now=h.top().id;h.pop();
if(vis[now])continue;
vis[now]=1;
for(int i=fir[now];i;i=nex[i])
{
int p=poi[i];
if(dis[p]>dis[now]+val[i])
{
dis[p]=dis[now]+val[i];
h.push((node){p,dis[p]});
}
}
}
线段树优化
和堆优差不多,通过线段树找到最小点权及其位置
走过的位置就设置成极大值
线段树上就维护单点修改和全局最小值查询
时间复杂度 \(O(m\log n)\)。
struct Seg_tree{
int le,ri;
int minn,id;
}tre[inf<<2];
void pushup(int i)
{
if(tre[i<<1].minn>tre[i<<1|1].minn)
tre[i].minn=tre[i<<1|1].minn,tre[i].id=tre[i<<1|1].id;
else tre[i].minn=tre[i<<1].minn,tre[i].id=tre[i<<1].id;
}
void build(int i,int l,int r)
{
tre[i].le=l;tre[i].ri=r;
if(l==r)
{
tre[i].minn=2139062143;
tre[i].id=l;
return;
}
int mid=(l+r)>>1;
build(i<<1,l,mid);
build(i<<1|1,mid+1,r);
pushup(i);
}
void change(int i,int id,int k)
{
if(tre[i].le==tre[i].ri)
{
tre[i].minn=k;
return;
}
int mid=(tre[i].le+tre[i].ri)>>1;
if(id<=mid)change(i<<1,id,k);
else change(i<<1|1,id,k);
pushup(i);
}
void dij(int s)
{
memset(dis,127,sizeof(dis));
dis[s]=0;change(1,s,0);
for(int i=1;i<n;i++)
{
int now=tre[1].id;
change(1,now,2139062143);
for(int i=fir[now];i;i=nex[i])
{
int p=poi[i];
if(dis[p]>dis[now]+val[i])
{
dis[p]=dis[now]+val[i];
change(1,p,dis[p]);
}
}
}
}
桶优化

图片来自 2021 年 NOIp 夏令营中孙铭远讲师的图论课件
代码是自己打的
while(1)
{
vis[now]=1;
for(int i=fir[now];i;i=nex[i])
{
int p=poi[i];
if(dis[p]>dis[now]+val[i])
{
dis[p]=dis[now]+val[i];
T[dis[p]].push_back(p);
maxn=max(maxn,dis[p]);
}
}
last=now;
for(int i=1;i<=maxn;i++)
{
if(T[i].size())
{
if(vis[T[i][0]]==0)now=T[i][0];
last=i;T[i].erase(T[i].begin());
break;
}
}
if(last==now)break;
}
SPFA(单源最短路)
SPFA 在国际上被称为 “队列优化的 Bellman-Ford ”算法 ,只是在中国被称为 "Shortest Path Faster Algorithm" ,简称 "SPFA" 。
而且

SPFA 的基本思路是:
先将源点入队,然后遍历源点发出的边,将其指向的点的 dis 值更新(如果能的话),然后源点出队。如果指向的点没有入队就将其入队。直到队列为空。
memset(dis,127,sizeof(dis));
dis[s]=0;h.push(s);
while(h.size())
{
int now=h.front();h.pop();
vis[now]=0;
for(int i=fir[now];i;i=nex[i])
{
int p=poi[i];
if(dis[now]+val[i]<dis[p])
{
dis[p]=dis[now]+val[i];
if(vis[p])continue;
vis[p]=1;h.push(p);
}
}
}
随机数据下,SPFA 的时间复杂度是 \(O(km)\),\(k\) 是一个常数,平均取 \(2\)。但在某些 hack 数据下,SPFA 会退化成 Bellman-Ford ,时间复杂度为 \(O(nm)\)。
SPFA 有很多优化,如:SLF 和 LLL 等,但都容易被卡。
但是 SPFA 也有自己的用处:
判负环
众所周知,判负环有两种方法:
-
原理:显然,对于一个没有负环的图,一个点最多松弛 \(n-1\) 轮。当一个点的入队次数超过 \(n\) 时,就存在负环。
做法:我们记录一个点的入队次数,当大于点数 \(n\) 时,判定存在负环。
bool spfa()
{
dis[1]=0;h.push(1);
while(h.size())
{
int now=h.front();h.pop();
vis[now]=0;
for(int i=fir[now];i;i=nex[i])
{
int p=poi[i];
if(dis[p]>dis[now]+val[i])
{
dis[p]=dis[now]+val[i];
num[p]++;
if(num[p]>n)return 1;
if(vis[p])continue;
h.push(p);vis[p]=1;
}
}
}
return 0;
}
-
原理:一个没有负环的图的最短路上的边数不超过 \(n\)。
做法:记录到当前点的最短路径的边数,当大于点数 \(n\) 时,判定存在负环。
bool SPFA()
{
dis[1]=0;h.push(1);
while(h.size())
{
int now=h.front();h.pop();
vis[now]=0;
for(int i=fir[now];i;i=nex[i])
{
int p=poi[i];
if(dis[p]>dis[now]+val[i])
{
dis[p]=dis[now]+val[i];
len[p]=len[now]+1;
if(len[p]>=n)return 1;
h.push(p),vis[p]=1;
}
}
}
return 0;
}
显然,第二种方法的时间复杂度更优。
差分约束系统
虽然洛谷有【模板】标签的不是它,但这个非官方模板比官方模板更有名气。
此算法与 差分 并无关联。
差分约束的形式 m 组 n 元一次不等式。
那么,不等式和最短路有什么关系呢?
回想最短路,我们做完所有松弛操作之后,对于每条边和其连接的两个点 \(u,v\),都有如下关系:
因为松弛操作就是将 \(dis_v>dis_u+val_{u,v}\) 的 \(v\) 点的点权更新。
再看题目中给的不等式:
- \(a-b\ge c\)
- \(a-b\le c\)
- \(a=b\)
整理一下,可以得到以下四个不等式:
- \(b\le a-c\)
- \(a\le b+c\)
- \(a\le b+0\)
- \(b\le a+0\)
结合最短路角度中的不等关系,就可以建图:
ins(b,a,-c);
ins(a,b,c);
ins(a,b,0);
ins(b,a,0);
为了防止图不连通导致的错误判断,差分约束都会建一个虚拟源点“0 点”,将所有的点都与 0 点相连,边权为 0,这样整个图就一定联通了。
即:
for(int i=1;i<=n;i++)
ins(0,i,0);
而这样为什么是对的呢?
这个操作就相当于加了一堆这样的不等式:
\(0\le a+0\)
显然,原本就成立的不等式加入到不等式组中对答案没有影响。
最后,在图上跑一遍 SPFA,当图中存在负环,则不等式组无解,否则每个点的 dis 值即为可能解。
对于差分约束而言,重点不在其本身如何解决,而在于这种图论建模的思想。
最小费用最大流
即 EK 算法。
Johnson(多源最短路)
简单来讲,Johnson 就是跑了 n 遍 Dij。
那么,时间复杂度就为 \(O(nm\log m)\)。
之前说过, Dij 不能处理含负边权的图的最短路问题。
题目描述:
- 边权可能为负,……
emm……
让我们观赏一下大型纪录片《SPFA的复活之路》
再往下看题目描述:
- 部分数据卡 n 轮 SPFA 算法
。。。换题
仔细想想,我们可以像差分约束一样,设置一个超级源点 0 点,而且 0 点到每个点的边权值也为 0。
先用一轮 SPFA 求出 0 点所有节点的最短路 \(h_i\)(顺便判一手负环)。之前的边权值 \(val_{u,v}\) 就可以更新为 \(val_{u,v}+h_u-h_v\)。
因为对于最短路上,有 \(val_{u,v}+h_u\ge h_v\),故 \(val_{u,v}+h_u-h_v\ge 0\),故无负权值存在,也就可以跑 n 轮堆优 Dij 去求解了。
这一步叫 re_weight :
void re_weight()
{
for(int i=1;i<=n;i++)
for(int j=fir[i];j;j=nex[j])
val[j]+=dis1[i]-dis1[poi[j]];
}
最后,再减去起点 \(h_s\) 并加上终点 \(h_t\),就是两个点之间的最短路了。
为什么呢?
设求出的一条最短路径为 \(s\rightarrow n_1\rightarrow n_2\cdots n_k\rightarrow t\)。
那么重赋值之后的最短路长度为
拆括号,化简得:
于是将得到的结果 \(-h_s+h_t\) 便是两点之间的最短路。
同时,也证明 Johnson 算法的正确性。
最短路计数
用 SPFA 或者堆优 Dij 都是可以的。
只需要加上递推式:
if(dis[p]==dis[now]+val[i])
num[p]+=num[now];
num 就表示最短路的条数。
整个就是这样:
memset(dis,127,sizeof(dis));
dis[1]=0;num[1]=1;
h.push(pr(dis[1],1));
while(h.size())
{
pr data=h.top();h.pop();
int now=data.second;
if(vis[now])continue;
vis[now]=1;
for(int i=fir[now];i;i=nex[i])
{
int p=poi[i];
if(dis[now]+val[i]==dis[p])
num[p]+=num[now];
if(dis[now]+val[i]<dis[p])
{
dis[p]=dis[now]+val[i];
num[p]=num[now];
h.push(pr(dis[p],p));
}
}
}
例题 ,记得取模。
最短路径
同样是可以用 SFPA 和堆优 Dij,在求最短路的时候记录下经过的点中 dis 最小的的前驱,最后再从终点反向搜回去。
像这样:
memset(dis,127,sizeof(dis));
dis[1]=0,vis[1]=1;
h.push(1);
while(h.size())
{
int now=h.front();h.pop();
vis[now]=0;
for(int i=fir[now];i;i=nex[i])
{
int p=poi[i];
if(dis[p]>dis[now]+val[i])
{
dis[p]=dis[now]+val[i];
pre[p]=now;
if(vis[p])continue;
h.push(p),vis[p]=1;
}
}
}
int now=n;
while(now!=1)
{
ans_.push_back(now);
now=pre[now];
}
ans_.push_back(1);
ans_ 就是反向存着的从 1 到 n 的最短路径。