平衡二叉树结构 AVL
它是在BST的基础上又加了限制条件,限制任一结点的左右子树的高度差不能大于1.也就是说AVL看起来要更加规整。
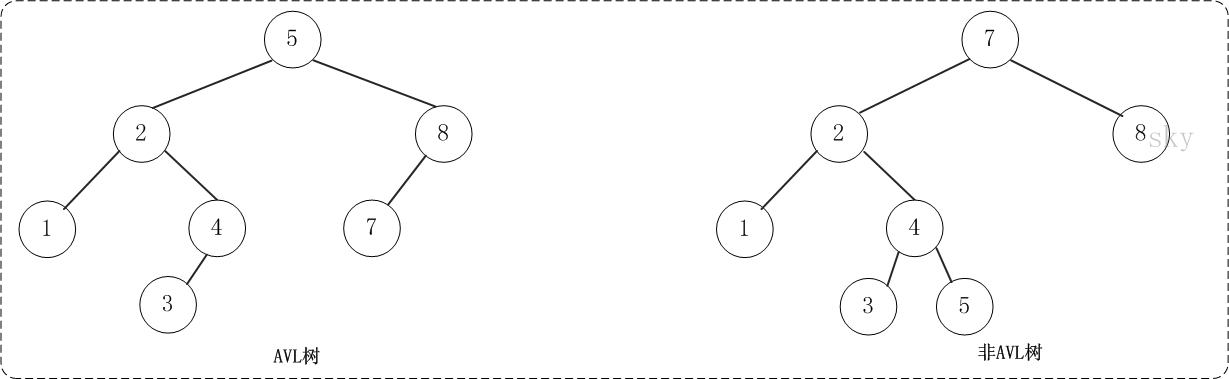 若理想情况--左右子树高度相等,其搜索时间复杂度为log(N),若不理想--线性树,时间复杂度变为O(N)。
AVL平衡失控的原因是因为加入了新结点。它有四种失衡状态:
若理想情况--左右子树高度相等,其搜索时间复杂度为log(N),若不理想--线性树,时间复杂度变为O(N)。
AVL平衡失控的原因是因为加入了新结点。它有四种失衡状态:
 AVL树失去平衡之后,可以通过旋转使其恢复平衡。下面分别介绍四种失去平衡的情况下对应的旋转方法。
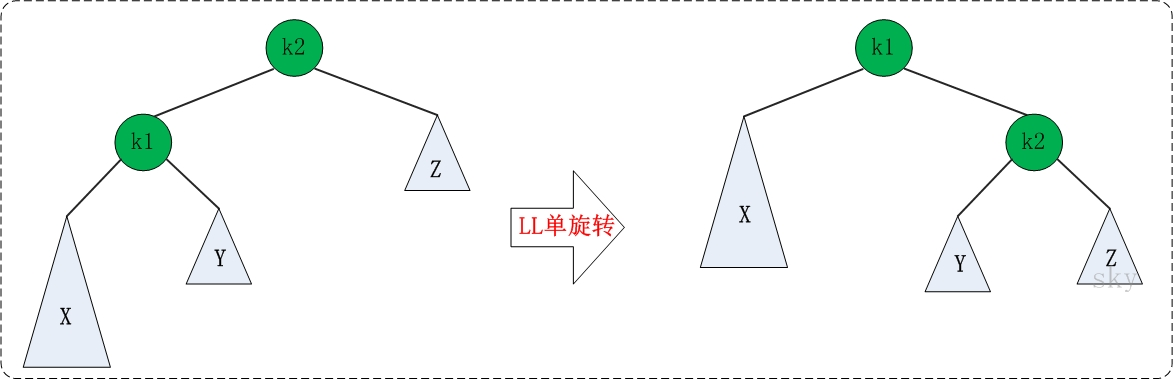
LL的旋转。LL失去平衡的情况下,可以通过一次旋转让AVL树恢复平衡。步骤如下:
AVL树失去平衡之后,可以通过旋转使其恢复平衡。下面分别介绍四种失去平衡的情况下对应的旋转方法。
LL的旋转。LL失去平衡的情况下,可以通过一次旋转让AVL树恢复平衡。步骤如下:
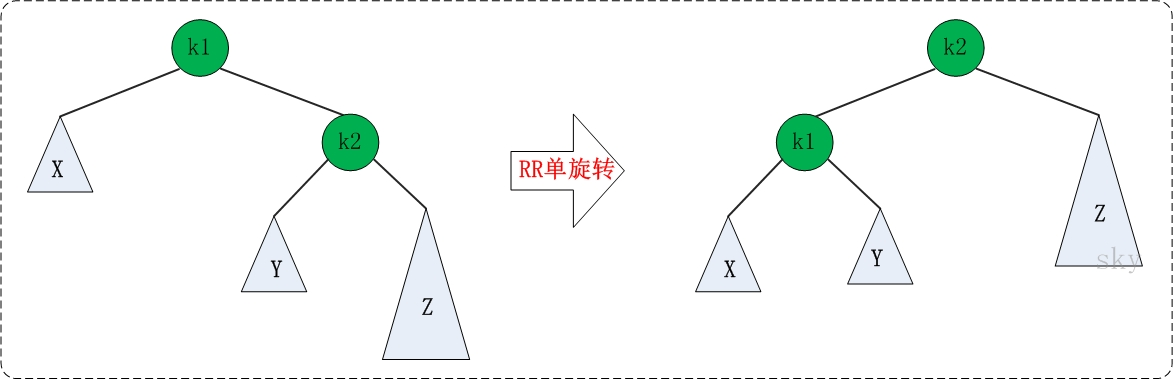
 RR的旋转:RR失去平衡的情况下,旋转方法与LL旋转对称,步骤如下:
RR的旋转:RR失去平衡的情况下,旋转方法与LL旋转对称,步骤如下:
 LR的旋转:LR失去平衡的情况下,需要进行两次旋转,步骤如下:
LR的旋转:LR失去平衡的情况下,需要进行两次旋转,步骤如下:
 RL的旋转:RL失去平衡的情况下也需要进行两次旋转,旋转方法与LR旋转对称,步骤如下:
RL的旋转:RL失去平衡的情况下也需要进行两次旋转,旋转方法与LR旋转对称,步骤如下:

 若理想情况--左右子树高度相等,其搜索时间复杂度为log(N),若不理想--线性树,时间复杂度变为O(N)。
AVL平衡失控的原因是因为加入了新结点。它有四种失衡状态:
若理想情况--左右子树高度相等,其搜索时间复杂度为log(N),若不理想--线性树,时间复杂度变为O(N)。
AVL平衡失控的原因是因为加入了新结点。它有四种失衡状态:
 AVL树失去平衡之后,可以通过旋转使其恢复平衡。下面分别介绍四种失去平衡的情况下对应的旋转方法。
LL的旋转。LL失去平衡的情况下,可以通过一次旋转让AVL树恢复平衡。步骤如下:
AVL树失去平衡之后,可以通过旋转使其恢复平衡。下面分别介绍四种失去平衡的情况下对应的旋转方法。
LL的旋转。LL失去平衡的情况下,可以通过一次旋转让AVL树恢复平衡。步骤如下:
- 将根节点的左孩子作为新根节点。
- 将新根节点的右孩子作为原根节点的左孩子。
- 将原根节点作为新根节点的右孩子。
 RR的旋转:RR失去平衡的情况下,旋转方法与LL旋转对称,步骤如下:
RR的旋转:RR失去平衡的情况下,旋转方法与LL旋转对称,步骤如下:
- 将根节点的右孩子作为新根节点。
- 将新根节点的左孩子作为原根节点的右孩子。
- 将原根节点作为新根节点的左孩子。
 LR的旋转:LR失去平衡的情况下,需要进行两次旋转,步骤如下:
LR的旋转:LR失去平衡的情况下,需要进行两次旋转,步骤如下:
- 围绕根节点的左孩子进行RR旋转。
- 围绕根节点进行LL旋转。
 RL的旋转:RL失去平衡的情况下也需要进行两次旋转,旋转方法与LR旋转对称,步骤如下:
RL的旋转:RL失去平衡的情况下也需要进行两次旋转,旋转方法与LR旋转对称,步骤如下:
- 围绕根节点的右孩子进行LL旋转。
- 围绕根节点进行RR旋转。





