浅谈 LCT

实链剖分和树链剖分的区别

树链剖分有一个更专业的名称：轻重链剖分，即为根据子节点的子树大小来剖，虽然树链剖分有很好的性质，但是还是存在缺陷的。例如：树链剖分将树剖完之后是静态的，（无法进行修改了，但不代表就不能换根了。）也就是说树链剖分只能针对于树的结构不变的情况下操作。

实链剖分：将树的边分为两种，一种是实边，一种是虚边，维护的时候则是对实边进行维护。

我们发现实链剖分很不固定，将树的边划分实虚的话，也无法保证形态。如果我们用一个灵活的数据结构，那么我们发现，其实这个树完全可以动起来，因为任意转化实虚边都可以维护，也就是说，删除一条边，加上一条边，对于实链剖分来说，都可以。

然后我们将实链剖分剖出来的链用 \(Splay\) 维护，这种数据结构叫做 \(LCT\) 即 \(Link-Cut-Tree\) 。

不知道为什么 \(LCT\) 的一些博客讲解中以 \(Splay\) 去维护轻重链剖分的链。

LCT 的一些浅显的概念理解

大概有辅助树， \(Splay\) 与辅助树的关系之类。

辅助树

可以简单的理解为一些 \(Splay\) 构成了辅助树。我们给出一张图来理解一下其结构：

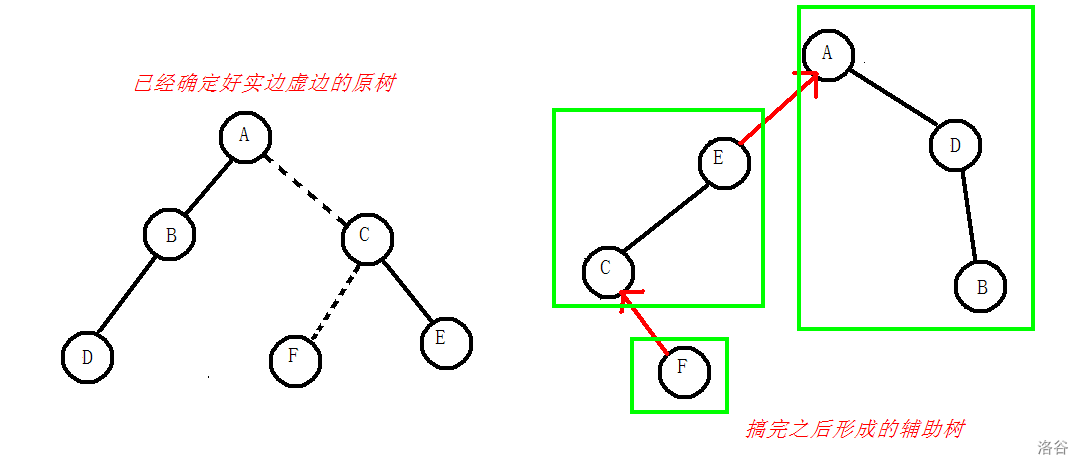
通过对比第一个图和第二个图，我们可以知道原树中的实链对应着辅助树的实链。无论怎么变换都是一条条的实链都是不会变得。

同时，因为我们选择用 \(Splay\) 维护一条实链，那么我们也就可以认为左边绿框框也就是一个 \(Splay\) , 然后我们显然可以知道这些 \(Splay\) 是通过虚边连接起来的（也就是红边连接起来的）。

然后我们考虑是怎么构造的这一颗辅助树：
首先我们通过实链构造出一颗颗的 \(Splay\) , 即为：

\(\{A - D - C \} ,\{ E - C \} , \{ F \}\) 总共三个 \(Splay\)

然后我们令 \(E , F\) 去寻找他在原树中的父亲，也就是 \(A , C\) , 然后通过虚边连接起来。
这里有一个不成文的规定： 认父不认子

最后就构造完了。

辅助树和原树的区别

辅助树的根不一定是原树的根。
原树父亲的指向不等同于辅助树父亲的指向
辅助树是可以在 \(Splay\) 的帮助下，实现任意换根。
辅助树中不存在节点指向子节点的情况。（但可以有节点统计子节点的情况）

LCT 的一些性质

每一个 \(Splay\) 维护的是一条在原树中深度严格递增的树链，且中序遍历 \(Splay\) 得到的每一个点的深度组成的序列也是严格递增的。

每一个节点包含且仅包含于一个 \(Splay\) 中

认父不认子

边分为实边和虚边，实边包含在 \(Splay\) 中，而虚边总是由一棵 \(Splay\) 指向另一个节点（指向该 \(Splay\) 中中序遍历最靠前的点在原树中的父亲）。
因为性质 \(2\)，当某点在原树中有多个儿子时，只能向其中一个儿子拉一条实链（只认一个儿子），而其它儿子是不能在这个 \(Splay\) 中的。
那么为了保持树的形状，我们要让到其它儿子的边变为虚边，由对应儿子所属的 \(Splay\) 的根节点的父亲指向该点，而从该点并不能直接访问该儿子（认父不认子）。

LCT 的一些操作

Access(x) 操作

因为性质 \(3\) ，建立了虚边，而我们选择维护的却是实链，所以会导致根节点 (以下均称为 \(rt\) ) 到 \(x\) 的路径经过所有的边不一定全都是实边，即 \(rt\) 到 \(x\) 的路径不通。
\(Access(x)\) 的意思为将 \(rt\) 到 \(x\) 的路径打通，也就是将 \(rt \to x\) 的路径上所有的经过的边都转化为实边。

这是 \(LCT\) 最核心的部分 ~~(就属 \(Splay\) 的代码最长)~~。

这里以 \(FlashHu\) 大佬的博文 LCT总结——概念篇中的例子予以说明。他讲的特别详细，我不认为我能比他讲的还要详细。

有一棵树，假设一开始实边和虚边是这样划分的（虚线为虚边）

那么所构成的 \(LCT\) 可能会长这样（绿框中为一个 \(Splay\)，可能不会长这样，但只要满足中序遍历按深度递增（性质 \(1\)）就对结果无影响）

现在我们要 \(Access(N)\)，把 \(A−N\) 的路径拉起来变成一条 \(Splay\)。
因为性质 \(2\) ，该路径上其它链都要给这条链让路，也就是把每个点到该路径以外的实边变虚。
所以我们希望虚实边重新划分成这样。

然后怎么实现呢？
我们要一步步往上拉。
首先把 \(splay(N)\)，使之成为当前 \(Splay\) 中的根。
为了满足性质 \(2\)，原来 \(N−O\) 的重边要变轻。
因为按深度O在N的下面，在 \(Splay\) 中O在 \(N\) 的右子树中，所以直接单方面将 \(N\) 的右儿子置为 \(0\)（认父不认子）
然后就变成了这样——

我们接着把 \(N\) 所属 \(Splay\) 的虚边指向的 \(I\)（在原树上是 \(L\) 的父亲）也转到它所属 \(Splay\) 的根，\(splay(I)\)。
原来在 \(I\) 下方的重边 \(I−K\) 要变轻（同样是将右儿子去掉）。
这时候 \(I−L\) 就可以变重了。因为 \(L\) 肯定是在 \(I\) 下方的（刚才 \(L\) 所属 \(Splay\) 指向了\(I\)），所以I的右儿子置为 \(N\)，满足性质 \(1\) 。
然后就变成了这样——

\(I\) 指向 \(H\)，接着 \(splay(H)\) ，\(H\) 的右儿子置为 \(I\) 。

\(H\) 指向 \(A\)，接着 \(splay(A)\)，\(A\) 的右儿子置为 \(H\) 。

\(A−N\) 的路径已经在一个 \(Splay\) 中了，大功告成！
代码其实很简单。。。。。。循环处理，只有四步——

归根到底，其实就是：
当 \(u\) 的右儿子为 \(v\) 的时候，我们就认为 \(u - v\) 是一条实边。
显然 \(Splay\) 是维护实链的，如果我们 \(1 \to n\) 是连通的，那么我们直接查询举行了。

同样的。如果不连通，那么就以为着我们需要将这一条链赋值成实链。我们按照上面图的模拟过程来即可。

模拟过程可以简化为：

旋转到当前 \(Splay\) 的根。
建立和父亲的实边关系。
更新节点维护的信息。

\(Question\) : 我们需不需要考虑当前和 \(u\) 这个点连接的实链，把他置换成虚边呢?
\(Answer\) : 不需要，这个时候就体现出我们认父不认子的好处了，我们直接将 \(u\) 这个点的右儿子替换掉，就代表 \(u\) 这个点的右儿子已经处理完了。

qaq void Access(int u) {
	for(qwq int y = 0 ; u ; u = f[y = u]) 
	 Splay(u) , ch[u][1] = y , pushup(u) ; 
	// 先旋转到当前 Splay 的根，然后通过 f[u] 建立的虚边找到父亲节点，同时将父亲节点
	// 的右儿子赋为当前的这个点，形成实边，同时连接该节点和父亲所在的 Splay  。
	// pushup 即为更新维护的信息 
}

MakeRoot(x) 操作

就像他的意译一样， \(MakeRoot\) ，使成为根。~~缺宾语~~

那么如何操作呢。我们上文已经知道了如何将打通一个点到根的路径了。

这时候用到 \(Access(x)\) 和 \(Splay(x)\) 操作了。

我们这个 \(Splay\) 满足性质 \(1\), 所以 \(Access(x)\) 之后， \(x\) 还是深度最大的点。

我们将其 \(Splay\) 旋转一下，本来它就是最大的，显然 \(x\) 在这个 \(Splay\) 中没有右子树。

于是我们翻转整个 \(Splay\) ，使得所有点的深度都倒过来，\(x\) 没有了左子树，它成了深度最小的点，那 \(x\) 其实不就是树根了嘛。

qaq void MakeRoot(int u) {
	Access(u) , Splay(u) , PushOver(u) ; 
	// PushOver(u) 就是翻转操作
}

FindRoot 操作

找树根。
\(Access(x)\) 之后 \(x\) 不就是深度最大的点了嘛，我们就不断去找左子树左子树，也就是去寻找深度最小的点，当节点 \(u\) 没有左子树的时候，他的深度也就是最小的了，那么 \(u\) 就是树根了。

当然，其中有可能会有 \(tag\) 标记，也就是区间翻转标记，我们这里直接下传即可，不下传无法保证 \(u\) 一定是树根。解释的话，分析上一个操作。

qaq void FindRoot(int u) {
	Access(u) ; 
	while(ch[u][0]) pushdown(u) , u = ch[u][0] ; 
	return u ; 
}

Link 操作

在 \(LCT\) 中加入一条 \(u - v\) 的边。

让 \(u\) 成为树根 , 然后建立虚边。

这个地方需要特判一下，因为树上显然不能出现环，所以 \(FindRoot(v) \neq u\) ,这样才让 \(u\) 向 \(v\) 认父。如果不知为什么 \(u\) 向 \(v\) 认父，则建议重新审视一下 \(Access(x)\) 的模拟过程。

qaq void Link(int u , int v) {
	MakeRoot(u) ; 
	if(FindRoot(v) != u) f[u] = v ; 
}

Split 操作

\(Split(u,v)\)代表是抽出 \(u - v\) 这条路径成为实链。

这时候我们有 \(Link\) 的启发，我们就可以直接让 \(u\) 成为树根。然后通过 \(Access(v)\) 打通\(u - v\) 的路径即可。

qaq void Split(int u , int v) {
	MakeRoot(u) , Access(v) , Splay(v) ;
}

Cut 操作

删除 \(u , v\) 这一条边。

如果题目保证断边合法，倒是很方便。

使 \(u\) 为根后， \(v\) 的父亲一定会指向 \(u\) , 且深度相差 \(1\) , 当 \(Access(v) , Splay(v)\) 之后，因为 \(u\) 深度小，所以 \(u\) 一定是 \(v\) 的左儿子。直接断开连接。

qaq void CUT(int u , int v) {
	Split(u , v) ; f[u] = ch[v][0] = 0 ; pushup(v) ;
}

如果题目不保证断边合法，也就是不一定会存在该边。

那么我们也按照上面一样，去特判一下。首先使得 \(u\) 成为 \(Splay\) 的根，然后去判断一下 \(u , v\) 是否在一个子树内，如果不在，则不存在。接着去判断一下 \(v\) 的父亲是否是 \(u\) ，如果不是，不存在，最后去判断一下 \(v\) 是否有左儿子，如果没有，也不行。

qaq void Cut(int u , int v) {
	MakeRoot(u) ; 
	if(FindRoot(v) == u && f[v] = u && !ch[v][0]) 
	f[v] = ch[u][1] = 0 ,pushup(u); 
}

Splay , Rorate，pushdown，其他操作

和普通平衡树很相似，但是有几处是不同的。

这里就直接给出代码了

qaq bool check(int x) {//判断节点是否为一个Splay的根（与普通Splay的区别1）
	return ch[f[x]][1] == x || ch[f[x]][0] == x ;
}//原理很简单，如果连的是轻边，他的父亲的儿子里没有它
qaq bool jd(int x) {
	return ch[f[x]][1] == x ; 
}
qaq void PushOver(int u) {
	swap(ch[u][1] , ch[u][0]) ;
	tag[u] ^= 1 ; 
}
qaq void pushdown(int u) {
	if(tag[u]) 
	{
		tag[u] = 0 ; 
		if(ch[u][0]) PushOver(ch[u][0]) ; 
		if(ch[u][1]) PushOver(ch[u][1]) ;
	}
}
qaq void Rorate(int x) {
	int y = f[x] , z = f[y] , k = ch[y][1] == x , w = ch[x][k ^ 1] ; 
	if(check(y)) ch[z][ch[z][1] == y] = x ; ch[x][k ^ 1] = y ; ch[y][k] = w ; 
	//额外注意if(check(y))语句，此处不判断会引起致命错误（与普通Splay的区别2）
	if(w) f[w] = y ;f[y] = x ; f[x] = z ; pushup(y) ; 
}
qaq void Splay(int x) {//只传了一个参数，因为所有操作的目标都是该Splay的根（与普通Splay的区别3）
	int y = x, z = 0 ; sta[++z] = y ; //sta为栈，暂存当前点到根的整条路径，pushdown时一定要从上往下放标记（与普通Splay的区别4）
	while(check(y)) sta[++z] = y = f[y] ; 
	while(z) pushdown(sta[z--]) ; 
	while(check(x)) 
	{
		y = f[x] , z = f[y] ; 
		if(check(y)) Rorate(jd(x) ^ jd(y) ? x : y) ; 
		Rorate(x) ; 
	}
	pushup(x) ; 
}

P3690 【模板】动态树（Link Cut Tree）

囊括了几乎上文所有内容。

因为上文都说了，所以这里也是直接给出代码了。不过这个是早写的，所以用的是结构体存的，不过没什么两样

//
/*
Author : Zmonarch
Knowledge :
*/
#include <bits/stdc++.h>
#define int long long
#define inf 2147483647
#define qwq register
#define qaq inline
using namespace std ;
const int kmaxn = 1e6 + 10 ;
qaq int read() {
	int x = 0 , f = 1 ; char ch = getchar() ;
	while(!isdigit(ch)) {if(ch == '-') f = - 1 ; ch = getchar() ;}
	while( isdigit(ch)) {x = x * 10 + ch - '0' ; ch = getchar() ;}
	return x * f ;
}
int n , m ; 
int f[kmaxn] , rt[kmaxn] , sum[kmaxn] , s[kmaxn]; 
struct SPLAY {
	int val , sum ; 
	bool tag ; // 区间翻转的标记 
	int ch[2] ; 
	SPLAY() {
	 tag = ch[1] = ch[0] = 0 ; 
	}
}st[kmaxn << 1];
qaq bool check(int x) {
	return (st[f[x]].ch[0] == x) || (st[f[x]].ch[1] == x) ; 
}
qaq void pushup(int u) {
	st[u].sum = st[u].val ^ st[st[u].ch[0]].sum ^ st[st[u].ch[1]].sum ;
}
qaq void Pushover(int u) {
	swap(st[u].ch[1] , st[u].ch[0]) ; 
	st[u].tag ^= 1 ; 
}
qaq void pushdown(int u) {
	if(st[u].tag)
	{
		if(st[u].ch[0]) Pushover(st[u].ch[0]) ; 
		if(st[u].ch[1]) Pushover(st[u].ch[1]) ;
		st[u].tag = 0 ;
	} 
}
qaq void Rorate(int x) {
	int y = f[x] , z = f[y] , k = (st[y].ch[1] == x) , w = st[x].ch[!k] ;
	if(check(y)) st[z].ch[st[z].ch[1] == y] = x ;
	st[x].ch[!k] = y ; st[y].ch[k] = w ; 
	if(w) f[w] = y ; f[y] = x ; f[x] = z ; pushup(y) ; 
}
qaq void Splay(int x) {
	int y = x , z = 0 ; rt[++z] = y ; 
	while(check(y)) rt[++z] = y = f[y] ; 
	while(z) pushdown(rt[z--]) ; 
	while(check(x)) 
	{
		y = f[x] ; z = f[y] ; 
		if(check(y)) Rorate((st[y].ch[0] == x) ^ (st[z].ch[0] == y) ? x : y) ;
		Rorate(x) ; 
	} 
	pushup(x) ;
}
qaq void Access(int u) {
	for(qwq int y = 0 ; u ; y = u , u = f[u]) 
	 Splay(u) , st[u].ch[1] = y , pushup(u) ; 
// 通过虚链指定父亲，将这个父亲旋转到当前父亲所在的 Splay 的根上，更新 u 这个点的右儿子。 
}
qaq void MakeRoot(int u) { // 指定 u 为原树的根 
	Access(u) ; Splay(u) ; Pushover(u) ; 
}
qaq int FindRoot(int u) {
	Access(u) ; Splay(u) ; 
	while(st[u].ch[0]) pushdown(u) , u = st[u].ch[0] ; 
	Splay(u) ; return u ;   
}
qaq void Split(int u , int v) { // 使得 u , v 这一条链能在一个 Splay 中 
	MakeRoot(u) ; Access(v) ; Splay(v) ; 
	// 先让 u 成为根，然后直接 Access 打通 v 到根 
}
qaq void Link(int u , int v) { // 判断连一条 u , v 的边是否合法  
	MakeRoot(u) ; 
	if(FindRoot(v) != u)  f[u] = v ; // u -> v 的边
	// u 已经是 Splay 的了，根据认父不认子，所以直接向这个根连 
}
// 这是保证存在该边的情况 
qaq void Cut(int u , int v) { // 断开 u - v 这条边 
	Split(u , v) ; f[u] = st[v].ch[1] = 0 ; pushup(u) ;  
}
// 这是不保证存在该边的情况
qaq void Pre_Cut(int u , int v) {
	MakeRoot(u) ; 
	if(FindRoot(v) == u && f[v] == u && !st[v].ch[0]) f[v] = st[u].ch[1] = 0 , pushup(u) ;  
}
signed main() {
	n = read() , m = read() ; 
	for(qwq int i = 1 ; i <= n ; i++) st[i].val = read() ; 
	for(qwq int i = 1 ; i <= m ; i++) 
	{
		int opt = read() , x = read() , y = read() ; 
		if(opt == 0) Split(x , y) , printf("%lld\n" , st[y].sum) ; 
		if(opt == 1) Link(x , y) ;
		if(opt == 2) Pre_Cut(x , y) ; 
		if(opt == 3) Splay(x) , st[x].val = y ; 
	}
	return 0 ;
}

题单

这里就是照搬 \(FlashHu\) 大佬的 LCT总结——应用篇（附题单）（LCT）这篇博客了。

\(ans \ \ so\ \ on…\)

鸣谢

LCT总结——概念篇
 OI-Wiki -- Link Cut Tree
LCT总结——应用篇（附题单）（LCT）

posted @ 2021-08-05 20:25 SkyFairy 阅读(285) 评论(3) 编辑收藏举报

刷新页面返回顶部

SkyFairy