模拟赛
【前序】:
本来看到题的时候,就知道这次显然是考不大行。
预测 : \(100 + 0 + 0\)
实际 : \(45\)
\(T1\) 板子题,写挂,身败名裂。
【带系数的 Fibonacci 】
搬到洛谷上 : Here
【description】:
已知 \(f_i = A \times f_{i - 1} + B \times f_{i - 2}\) , 求解 \(f_n\) 答案对 \(7\) 取模 。
【solution】:
直接板子题,模数特别小,显然是不会炸掉的。
身败名裂1 : 少跑了一遍快速幂。
矩阵 :
绝了,我写成了 \(quick(a , n - 3)\) 少跑了一遍快速幂,样例还过了,真气人啊。
【Code】:
/*
Author : Zmonarch
Knowledge :
*/
#include <bits/stdc++.h>
#define inf 2147483647
#define qwq register
#define int long long
#define qaq inline
const int kmaxn = 1e6 + 10 ;
const int mod = 7 ;
qaq int read() {
int x = 0 , f = 1 ; char ch = getchar() ;
while(!isdigit(ch)) {if(ch == '-') f = - 1 ; ch = getchar() ;}
while( isdigit(ch)) {x = x * 10 + ch - '0' ; ch = getchar() ;}
return x * f ;
}
int A , B , n ;
struct Matrix {
int n , m , a[3][3] ;
Matrix() {n = m = 0 ; memset(a , 0 , sizeof(a)) ;}
};
Matrix operator * (const Matrix &m1 , const Matrix &m2) {
Matrix m3 ; m3.n = m1.n ; m3.m = m2.m ;
for(qwq int i = 1 ; i <= m3.n ; i++)
for(qwq int j = 1 ; j <= m3.m ; j++)
for(qwq int k = 1 ; k <= m1.m ; k++)
m3.a[i][j] = (m3.a[i][j] + m1.a[i][k] * m2.a[k][j]) % mod ;
return m3 ;
}
Matrix quick(Matrix a , int b) {
Matrix ret ; ret.m = 2 ; ret.n = 2 ;
for(qwq int i = 1 ; i <= 2 ; i++) ret.a[i][i] = 1 ;
while(b)
{
if(b & 1) ret = ret * a ;
a = a * a ; b >>= 1 ;
}
return ret ;
}
signed main() {
A = read() % mod , B = read() % mod , n = read() ;
if(n <= 2) {printf("1\n") ; return 0 ;}
Matrix ans ; ans.n = 1 ; ans.m = 2 ;ans.a[1][1] = 1 ; ans.a[1][2] = 1 ;
Matrix a ; a.m = a.n = 2 ;
a.a[1][1] = 0 ; a.a[1][2] = B ;
a.a[2][1] = 1 ; a.a[2][2] = A ;
ans = ans * quick(a , n - 2) ;
printf("%lld\n" , ans.a[1][2]) ;
return 0 ;
}
【某站队问题】
搬到洛谷 : Here
【description】 :
给定 \(n\) 个 \(1\) , \(m\) 个 \(0\) , 构造一个 \(01\) 串,使其合法的概率。
合法表示在任意的一个位置 \(i\) , 都有前 \(i - 1\) 个中 \(1\) 个数大于等于 \(0\) 的个数。
\(n , m\leq 2\times 10^5\)
【solution】 :
\(1.\) 打表找规律。 \(ans = \frac{n - m + 1}{n + 1}\)
\(2.\) 用脑子想 。
来源 caq 转
结论题。
我们可以构建一个二维坐标系,求总的方案书我们就可以抽象成 \(\dbinom{n+m}{m}\)。
我们设一个物理老师为 \(P\),设一个生物老师为 \(E\)。
如果我们往序列中添加了一个 \(P\),那就是横坐标 \(+1\) ,如果是往序列中添加了个 \(E\),那就是纵坐标 \(+1\)。
无良商家转载图片Ing.
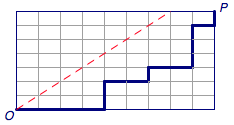
我们可以发现,如果方案是合法的,那么一定会在 \(y=x\) 这个直线或者其以下,但是这种情况并不好弄,所以我们思考别的方式来做它。
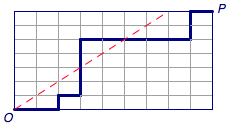
看这个图,他越界了,我们突然发现越界的有一个非常非常重要的性质,那就是一定会至少有一条这样的竖线(\(|\))会下边连接在 \(y=x\) 上,上面到了越界的点,那么我们把这个线翻转下来,然后把后面的再拼上去,就变成了下面这个情况
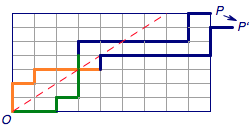
不用看前面的翻转啊,那个不是,只看绿橙相交的那个点就可以啦。
我们发现,一旦翻转之后,最终的点就变成了 \((n+1,m-1)\),
可以发现每一个不合法的方案都具有这种性质(我们只需要翻转一条这样的线即可),那么我们寻找一下走到这个点的方案数 \(\dbinom{n+m}{m-1}\),减去就是合法的方案数。
但是这个题目是求概率啊,所以就直接?求出不合法的概率减去就可以了。
即可得出答案。
【Code】:
/*
Author : Zmonarch
Knowledge :
*/
#include <bits/stdc++.h>
#define inf 2147483647
#define qwq register
#define int long long
#define qaq inline
const int kmaxn = 1e6 + 10 ;
const int mod = 7 ;
qaq int read() {
int x = 0 , f = 1 ; char ch = getchar() ;
while(!isdigit(ch)) {if(ch == '-') f = - 1 ; ch = getchar() ;}
while( isdigit(ch)) {x = x * 10 + ch - '0' ; ch = getchar() ;}
return x * f ;
}
signed main() {
int T = read() ;
for(qwq int oi = 1 ; oi <= T ; oi++)
{
int n = read() , m = read() ;
if(n < m) printf("%.6lf\n" , (double)0) ;
else printf("%.6lf\n" , (double)(n - m + 1) / (n + 1)) ;
}
return 0 ;
}
【“化学”竞赛的大奖】:
【description】:
\(XYX\) 在 \(CChO\) (全国化学奥林匹克竞赛)比赛中获得了大奖,奖品是一张特殊的机票。
使用这张机票,可以在任意一个国家内的任意城市之间的免费飞行,只有跨国飞行时才
会有额外的费用。\(XYX\) 获得了一张地图,地图上有城市之间的飞机航班和费用。已知从
每个城市出发能到达所有城市,两个城市之间可能有不止一个航班。一个国家内的每两
个城市之间一定有不止一条飞行路线, 而两个国家的城市之间只 有一条飞行路线。 \(XYX\)
想知道, 从每个城市出发到额外费用最大的城市, 以便估算出出行的费用, 请你帮助他。
当然,你不能通过乘坐多次一个航班增加额外费用, 也就是必须沿费用最少的路线飞
行。
【solution】 :
显然根据题目,一个强连连通分量代表一个国家。
身败名裂2:缩点不会写了,呜呜呜 , dfs 还 TM 写挂了
然后直接缩点形成一个个国家,反正在一个国家内不会有任何费用,不会对答案产生任何贡献。
缩点完之后显然是一棵树,求一点能到达的点的路径权值和最大 , 显然按照树的直径跑即可。
没调过的代码;
【Code】
/*
Author : Zmonarch
Knowledge :
*/
#include <bits/stdc++.h>
#define inf 2147483647
#define int long long
#define qwq register
#define qaq inline
using namespace std ;
const int kmaxn = 1e6 + 10 ;
inline int read() {
int x = 0 , f = 1 ; char ch = getchar() ;
while(!isdigit(ch)) {if(ch == '-') f = - 1 ; ch = getchar() ;}
while( isdigit(ch)) {x = x * 10 + ch - '0' ; ch = getchar() ;}
return x * f ;
}
int n , m , cnt , top , tot , TOT , Max , rt , sum;
struct node {
int nxt , u , v , w ;
}e[kmaxn << 1];
struct Newnode{
int nxt , u , v , w ;
}E[kmaxn << 1] ;
int h[kmaxn << 1] , H[kmaxn << 1] , low[kmaxn] , dfn[kmaxn] , st[kmaxn] , in[kmaxn] , scc[kmaxn] , dis[kmaxn] , Dis[kmaxn];
qaq void adde(int u , int v , int w) {
e[++tot].nxt = h[u] ;
e[tot].u = u ;
e[tot].v = v ;
e[tot].w = w ;
h[u] = tot ;
}
qaq void addE(int u , int v , int w) {
E[++TOT].nxt = H[u] ;
E[TOT].u = u ;
E[TOT].v = v ;
E[tot].w = w ;
H[u] = TOT ;
}
qaq void Tarjan(int u) //tarjan模板
{
dfn[u] = low[u] = ++ sum ;
st[++top] = u ;
for(int i = h[u] ; i ; i = e[i].nxt)
{
int v = e[i].v ;
if(!dfn[v])
{
Tarjan(v) ;
low[u] = min (low[u] , low[v]) ;
}
else if (!in[v]) low[u] = min (low[u] , dfn[v] ) ;
}
if(low[u] == dfn[u])
{
in[u] = ++ cnt ;
while(st[top + 1] != u)
{
++scc[cnt] ;
in[st[top]] = cnt ;
//printf("%d " , st[top]) ;
top -- ;
}
//printf("Fuck : %lld\n" , scc[cnt]) ;
}
}
qaq void dfs1(int u , int fa) {
// printf("%lld\n" , u) ;
for(qwq int i = H[u] ; i ; i = E[i].nxt)
{
int v = E[i].v ;
printf("Fuck : %lld %lld\n" , u , v) ;
if(v == fa) continue ;
dis[v] = dis[u] + E[i].w ;
//printf("%lld\n" , dis[v]) ;
if(dis[v] > Max) Max = dis[v] , rt = v ;
dfs1(v , u) ;
}
}
qaq void dfs2(int u , int fa) {
for(qwq int i = H[u] ; i ; i = E[i].nxt)
{
int v = E[i].v ;
if(v == fa) continue ;
Dis[v] = Dis[u] + E[i].w ;
dfs2(v , u) ;
}
}
signed main() {
n = read() , m = read() ;
for(qwq int i = 1 ; i <= m ; i++)
{
int u = read() , v = read() , w = read() ;
adde(u , v , w) ; //adde(v , u , w) ;
}
for(qwq int i = 1 ; i <= n ; i++)
if(!dfn[i]) Tarjan(i) ;
//memset(h , 0 , sizeof(h)) ;
for(qwq int i = 1 ; i <= m ; i++)
{
if(in[e[i].u] != in[e[i].v])
{
//printf("%lld %lld %lld\n" , in[e[i].u] , in[e[i].v] , e[i].w) ;
addE(in[e[i].u] , in[e[i].v] , e[i].w) ;
addE(in[e[i].v] , in[e[i].u] , e[i].w) ;
}
}
dfs1(1 , - 1) ; Max = 0 ;
memset(dis , 0 , sizeof(dis)) ;
printf("Fuck : %lld\n" , rt) ;
dfs1(rt , - 1) ; dfs2(rt , - 1) ;
//for(qwq int i = 1 ; i <= n ; i++) printf("%lld\n" , dis[in[i]]) ;
//dis[1] ;
//for(qwq int i = 1 ; i <= n ; i++)
// printf("%lld\n" , max(dis[in[i]] , Dis[in[i]])) ;
return 0 ;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号