简谈平衡树(Treap , Splay)
先谈
Treap
首先,要知道什么是 \(BST\) , 就是一个二叉查找树,更准确的来说,是一个按照关键字排序的一个堆,他具有十分良好的性质,那同时,在有的时候,会因为输入的数据为单调递增或者递减,从而退化成一条链,那么也就将我们本来 \(O(\log N)\) 查询一下子变成了 \(O(N)\) 的,那么很显然我们不如不用,直接写个数组都比这个好。
那么 \(Treap\) 就是通过旋转来维护平衡树的深度,令其尽量保持在 \(O(\log N)\) 同时使得平衡树可以满足一个按照关键字排序的性质 。
定义
旋转
正经人谁还分出开说

旋转的意义就是我尽量让他这个树平衡一下,同时你要维持这个关键字的顺序不变。由于 二叉树是一个中序遍历(先访问左节点,然后访问根节点,最后访问右节点)按照关键字的顺序排序的。
我们为了使其能够保持这个良好的性质,我们才出现了旋转。
进一步看一下这个旋转(还好不是 \(Splay\) 的旋转)
右旋
旋转相对于根节点来说的。
为了保持原来的 \(D < B < E < A < C\) 的一个性质,我们就让 \(A\) 向下走的时候,由于 \(E\) 比 \(A\) 要小,所以我们让 \(E\) 成为 \(A\) 的一个左节点,同时由于一个根节点和它的左节点一定小于它的右节点的左节点这么一个良好的性质(很显然吧),那么也就是说 \(B\) 上来, \(D,B\) 也一定小于 \(E\) , 因为 \(D < B\) ,让 \(D\) 成为 \(B\) 的左节点,同理, \(A,C\) 一样。不再赘述了
inline void rrorate(int &now) //右旋,right_rorate
{
int tmp = tree[now].l ; //左节点往上旋
tree[now].l = tree[tmp].r ;
tree[tmp].r = now ;
now = tmp ;
}
左旋
和右旋一样,相当于右旋的逆操作。
inline void lrorate(int &now) // 左旋 left_rorate
//加一个 & 是为了同时可以改变 main 函数中的 now 值
{
int tmp = tree[now].r ; //取出该点的右节点,让其往上旋,形成根节点
tree[now].r = tree[tmp].r; //本来的根节点下传了,那即将成为根节点的右节点就需要摆脱本来这个节点的右节点,给根节点
tree[tmp].l = tree[now].l;
now = tmp ;
}
随机化创造平衡条件
我们再搞一个图 :

\(Treap\) 是单旋
我们很显然的可以看到 \(Treap\) 是非常合理的,不过,这个只是单旋,
那么怎么算是合理的
随机化的来源
\(Bst\) 在随机数据下是接近平衡的,也就是隶属于 \(O(\log N)\) 的复杂度。那么 \(Treap\) 的思想就是利用 "随机" 来创造平衡条件,因为在旋转过程中必须维持 \(Bst\) 的性质,所以 \(Treap\) 就把 "随机" 放到了堆性质上。
应用该随机化
\(Treap = Tree + Heap\) ,\(Treap\) 在每插入一个新的节点的时候,我们给该节点随机一个额外的权值,然后再和二叉树的插入过程一样,自底向上的以此检查,当某一个节点不满足大根堆得时候,我们将其进行旋转。
同样的,对于删除一个节点,我们找到需要删除的点,我们将其旋转到叶子节点,然后进行删除,防止你删除该点之后,再进行寻找前面的时候断了联系。这就得不偿失了。
删除节点操作:把该点旋转至叶子节点后删除
一些定义类
- \(value\) 表示随机化出来的关键字
- \(cnt\) 表示每一个节点的副本数(与其相同的数字)
- \(date\) 表示本来给予的权值
插入操作
首先我们随机化插入 \(value\) 这个值,我用的是 \(rand\times rand\) ,我闲得慌,然后我们可以类比一下线段树的左右区间之类的,我们也是一样的,我们维护一下二叉堆,同时我们判断一下我们给出的随机值是否满足二叉堆的性质。通过左旋和右旋来进行一下调整,将 层数尽量的转化成 \(\log N\) 层,就是像上面的图一样,防止形成一条链
inline void insert(int &now , int data)
{
if(now == 0)
{
now = ++cnt ;
tree[now].size = 1 , tree[now].date = data , tree[now].value = rand() % kmod ;
return ;
}
tree[now].size++ ; //节点数加一
if(data >= tree[now].date) insert(tree[now].r , data) ;
else insert(tree[now].l , data) ;//维护堆的性质
//需要进行旋转,防止成链,其实你改改这个地方,T上几次就知道了
if(tree[now].l && tree[now].value > tree[tree[now].l].value) rrorate(now);
if(tree[now].r && tree[now].value > tree[tree[now].r].value) lrorate(now);
}
删除操作
为了防止我们删除一个节点之后导致整个平衡树失调了,也就是不满足平衡树的基本性质了,我们选择用旋转(左旋和右旋)将要删除的节点直接转移到叶子节点,那样我们也就能够直接删除并且保证无任何后效性。
void remove(int &now , int data) //删除一个节点
{
tree[now].size -- ;
if(tree[now].date == data) //找到了应该删除的点 ,同时我们需要将其旋转至叶子节点之后删除
{
if(!tree[now].l && !tree[now].r) {now = 0 ; return ;} //已经整成叶子节点
if(!tree[now].l || !tree[now].r) {now = tree[now].l + tree[now].r ; return ;}
if(tree[tree[now].l].value < tree[tree[now].r].value) //继续旋转,直至叶子节点
{
rrorate(now) , remove(tree[now].r , data) ;
return ;//转化了删除的节点了,因为你已经旋转了
}
else
{
lrorate(now) , remove(tree[now].l , data) ;
return ;
}
}
if(tree[now].date >= data) remove(tree[now].l , data) ; //类似于线段树的查询一样
else remove(tree[now].r , data) ; //没有找到就继续去找
}
例题 :普通平衡树
模板题。
【solution】
【给出《算法竞赛进阶指南》的解析】:
根据题意,在数据中可能会存在相同的数值,但是在平衡树中,很显然是不能存在相同的数值,我们还要求解排名和前驱之类的,所以我们需要开一个 \(cnt\) 记录一下,在计算排名的时候,就是 \(rank_i = \sum_{k=1}^{i} cnt\)
Code : Treap
/*
By : Zmonarch
知识点 :
直接用C++提交,C++11会出现一些CE的错误
*/
#include <iostream>
#include <cstdio>
#include <cstring>
#include <cmath>
#include <queue>
#include <stack>
#include <map>
#include <set>
#include <algorithm>
#include <time.h>
#define int long long
#define inf 2147483647
const int kmaxn = 1e6 + 10 ;
const int kmod = 1e9 + 7;
namespace Base
{
inline int Min(int a , int b) {return a < b ? a : b ;}
inline int Max(int a , int b) {return a < b ? b : a ;}
inline int Gcd(int a , int b) {return !b ? a : Gcd(b , a % b) ;}
inline int Abs(int a) {return a < 0 ? - a : a ;}
}
inline int read()
{
int x = 0 , f = 1 ; char ch = getchar() ;
while(!isdigit(ch)) {if(ch == '-') f = - 1 ; ch = getchar() ;}
while( isdigit(ch)) {x = x * 10 + ch - '0' ; ch = getchar() ;}
return x * f ;
}
int cnt , m , root ;
struct Treap
{
int date , value , l , r , size ;
//date表示原来的树上的节点的值,value 为随机值 , l为左节点, r 为右节点 , size 为节点的大小
}tree[kmaxn] ;
//更新子节点的个数
inline void up(int now) {tree[now].size = tree[tree[now].l].size + tree[tree[now].r].size + 1 ;}
inline void lrorate(int &now) // 左旋 left_rorate
//加一个 & 是为了同时可以改变 main 函数中的 now 值
{
int tmp = tree[now].r ; //取出该点的右节点,让其往上旋,形成根节点
tree[now].r = tree[tmp].l; //本来的根节点下传了,那即将成为根节点的右节点就需要摆脱本来这个节点的右节点,给根节点
tree[tmp].l = now;
tree[tmp].size = tree[now].size ;
up(now) ;
now = tmp ;
}
inline void rrorate(int &now) //右旋,right_rorate
{
int tmp = tree[now].l ; //左节点往上旋
tree[now].l = tree[tmp].r ;
tree[tmp].r = now ;
tree[tmp].size = tree[now].size ;
up(now) ;
now = tmp ;
}
void insert(int &now , int data)
{
if(now == 0)
{
now = ++cnt ;
tree[now].size = 1 , tree[now].date = data , tree[now].value = rand() % kmod ;
return ;
}
tree[now].size++ ; //节点数加一
if(data >= tree[now].date) insert(tree[now].r , data) ;
else insert(tree[now].l , data) ;//维护堆的性质
//需要进行旋转,也就是节点不满足堆的性质
if(tree[now].l && tree[now].value > tree[tree[now].l].value) rrorate(now);
if(tree[now].r && tree[now].value > tree[tree[now].r].value) lrorate(now);
up(now) ;
}
void remove(int &now , int data) //删除一个节点
{
tree[now].size -- ;
if(tree[now].date == data) //找到了应该删除的点 ,同时我们需要将其旋转至叶子节点之后删除
{
if(!tree[now].l && !tree[now].r) {now = 0 ; return ;} //已经整成叶子节点
if(!tree[now].l || !tree[now].r) {now = tree[now].l + tree[now].r ; return ;}
if(tree[tree[now].l].value < tree[tree[now].r].value)
{
rrorate(now) , remove(tree[now].r , data) ;
return ;
}
else
{
lrorate(now) , remove(tree[now].l , data) ;
return ;
}
}
if(tree[now].date >= data) remove(tree[now].l , data) ;
else remove(tree[now].r , data) ; //没有找到就继续去找
up(now) ;
}
int rank(int now , int data)
{
if(!now) return 0 ;
if(data > tree[now].date) return tree[tree[now].l].size + 1 + rank(tree[now].r , data);
return rank(tree[now].l , data) ;
}
int find(int now , int rank_)
{
if(rank_ == tree[tree[now].l].size + 1) return tree[now].date ;
if(rank_ > ( tree[tree[now].l].size + 1 ) ) return find(tree[now].r , rank_ - tree[tree[now].l].size - 1) ;
return find(tree[now].l , rank_) ;
}
int query_pre(int now , int data)
{
if(!now) return 0 ;
if(tree[now].date >= data) return query_pre(tree[now].l , data) ;
int tmp = query_pre(tree[now].r , data) ;
if(!tmp) return tree[now].date ;
else return tmp ;
}
int query_suf(int now , int data)
{
if(!now) return 0 ;
if(tree[now].date <= data) return query_suf(tree[now].r , data) ;
int tmp = query_suf(tree[now].l , data) ;
if(!tmp) return tree[now].date ;
return tmp ;
}
signed main()
{
//freopen("P3369_3.in", "r" , stdin) ;
srand(kmod) ;
m = read() ;
for(int opt , x , i = 1 ; i <= m ; i++)
{
opt = read() , x = read() ;
if(opt == 1) insert(root , x) ;
if(opt == 2) remove(root , x) ;
if(opt == 3) printf("%lld\n" , rank(root , x) + 1) ;
if(opt == 4) printf("%lld\n" , find(root , x)) ;
if(opt == 5) printf("%lld\n" , query_pre(root , x)) ;
if(opt == 6) printf("%lld\n" , query_suf(root , x)) ;
}
return 0 ;
}
Splay
上文的 \(Treap\) 是基于随机化来平摊复杂度,但是笔者并不是特别喜欢随机化,同样和笔者不喜欢随机化的人不少,有 \(Splay\) ,也叫做伸展树,这个是基于旋转的,但同时,这个没有上述那般好理解了。
旋转
旋转操作是 \(Spaly\) 最重要的操作,是维护其层数的有效手段,这么说吧,每当插入一个新的节点的时候,我们直接插入该节点,然后旋转到根节点,有的时候,有人会认为旋转后我们尽量的让那些对答案有贡献的尽可能的靠近根节点,但是吧,你不断的旋转,维护这些显然有些鸡肋了,我们的查询复杂度为 \(\log N\) 的,有些得不偿失了。
同时 \(Splay\) 我这里是没有用 \(l,r\) 的,直接用 \(child_{0|1}\) 来表示左孩子还是右孩子。
首先为什么要引入旋转,单旋已经满足不了了,我们以图来表示一下。

但是显然我们这么旋转并没有起到非常显著的效果,我们将 只旋转需要旋转到根节点的旋转方法 称为单旋,这么说吧,我们插入一个节点 \(now\) ,我们一直旋转旋转 \(now\) 这个节点(首先我们是明确的,你哪怕你自己一个节点旋转也是可以旋转到根节点的),如果我们在旋转到根节点的过程中,有其他的节点旋转了(我说过了,旋转是相对于根来说的) ,我们就说这种旋转方法为双旋,否则我们称为单旋。
双旋 :
- 如果节点到父亲和父亲到爷爷的方向是一致的 的时候,我们先旋转父亲,然后再旋转当前节点
- 如果方向不一致的时候,我们旋转两次当前节点 。
另外 : 在 \(n > 3\) 的时候,双旋降低树高是很明显的,但这里不给图了,一是时间有点急,而是也不想在机房这个 \(XP\) 上画图,很麻烦 。
了解一下双旋的操作 :
首先我们要知道我们 \(Splay\) 旋转,旋转到根节点。

我们把 \(z\) 固定住,开始移动三个点(好看,如果直接移动4个点,很麻烦)
x是y的左儿子,所以x < y
y是z的左儿子,所以y < z
所以x < z,所以如果要x弄到y的上面去的话,x就应该放到y的那个位置
继续看,现在y > x那么y一定是x的右儿子
但是X已经有了右儿子B,
根据平衡树我们可以知道X < B < Y
所以我们可以把X的右儿子B丢给Y当做左儿子
而X的左儿子A有A < X < Y < Z显然还是X的左儿子
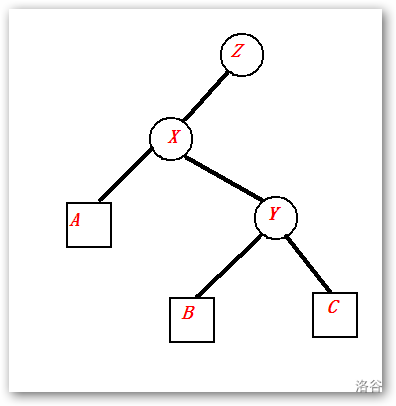
我们综合上述的情况 :
- 如果节点到父亲和父亲到爷爷的方向是一致的 的时候,我们先旋转父亲,然后再旋转当前节点
- **如果方向不一致的时候,我们旋转两次当前节点 **
Code : Splay
题目链接就是上面的题目 P3369 【模板】普通平衡树
/*
By : Zmonarch
知识点 :
*/
#include <iostream>
#include <cstdio>
#include <cstring>
#include <cmath>
#include <queue>
#include <stack>
#include <map>
#include <set>
#include <algorithm>
#define int long long
#define inf 2147483647
const int kmaxn = 1e6 + 10 ;
const int kmod = 998244353 ;
namespace Base
{
inline int Min(int a , int b) {return a < b ? a : b ;}
inline int Max(int a , int b) {return a < b ? b : a ;}
inline int Gcd(int a , int b) {return !b ? a : Gcd(b , a % b) ;}
inline int Abs(int a) {return a < 0 ? - a : a ;}
}
inline int read()
{
int x = 0 , f = 1 ; char ch = getchar() ;
while(!isdigit(ch)) {if(ch == '-') f = - 1 ; ch = getchar() ;}
while( isdigit(ch)) {x = x * 10 + ch - '0' ; ch = getchar() ;}
return x * f ;
}
int n , root , cnt ;
struct Splay
{
int ch[2] ;
int sum , fa , val , cnt;
}tree[kmaxn] ;
void update(int now) {tree[now].sum = tree[tree[now].ch[0]].sum + tree[tree[now].ch[1]].sum + tree[now].cnt ;}//和Treap一样
int check(int now) {return tree[tree[now].fa].ch[1] == now ; } ; //判断一下当前节点是其父亲的左节点还是右节点。
void connect(int now , int f , int to) {tree[now].fa = f ; tree[f].ch[to] = now ; } //由于是不断的在旋转,通过这个把当前的节点和其父亲建立联系
void rorate(int x) //执行旋转操作
{
int y = tree[x].fa , z = tree[y].fa ;
int yson = check(x) , zson = check(y) ;
//取出节点到父亲和父亲到爷爷的方向。
connect(tree[x].ch[yson ^ 1] , y , yson) ;
connect(y , x , yson ^ 1) ;
connect(x , z , zson) ;
update(y) , update(x) ;
}
void splay(int now , int goal) //把节点旋转到目标位置
{
int fa ; //= tree[now].fa ;
while((fa = tree[now].fa) != goal)
{
//我们取出节点到父亲和父亲到爷爷之间的距离,
//如果方向一样的话,我们就直接旋转父亲然后旋转节点
//如果方向不一样的话, 我们旋转两次节点
if(tree[fa].fa != goal) // 到了目标就不旋了
{
if(check(now) == check(fa)) rorate(fa) ;
else rorate(now) ;
}
rorate(now) ;
}
if(!goal) root = now ;
}
void insert(int data)
{
int now = root , fa = 0 ;
while(now && tree[now].val != data) fa = now , now = tree[now].ch[data > tree[now].val] ;
//我插入的值,如果我现在没有找到,那么我们可以根据二叉树进行寻找,更明白的,我们可以通过递归实现,均可以
if(now) tree[now].cnt++ ; //如果now不为0,那么说明tree[now].val = data ,不然不会跳出while
else // 否则我需要建立新的节点
{
now = ++cnt ;
tree[now].cnt = tree[now].sum = 1 ;
tree[now].val = data , tree[now].fa = fa ;
if(fa) connect(now , fa , data > tree[fa].val) ;
}
splay(now , 0) ;
}
int rank(int x)
{
if(tree[root].sum < x) return 0 ; //根本就没有 k 这个排名
int now = root ;
while(1)
{
int y = tree[now].ch[0] ;
if(x > tree[y].sum + tree[now].cnt) x -= tree[y].sum + tree[now].cnt , now = tree[now].ch[1] ;
else if(x <= tree[y].sum) now = y ;
else return tree[now].val ;
}
}
void Find(int x)
{
int now = root ;
while(tree[now].ch[x > tree[now].val] && tree[now].val != x) now = tree[now].ch[x > tree[now].val] ;
splay(now , 0) ;
}
int query_pre(int x)
{
Find(x) ; //tree[root].val这个是个平衡树,root.val就是最大的点值
if(tree[root].val < x) return root ;
int now = tree[root].ch[0] ;
while(tree[now].ch[1]) now = tree[now].ch[1] ;
return now ;
}
int query_suf(int x)
{
Find(x) ;
if(tree[root].val > x) return root ;
int now = tree[root].ch[1] ;
while(tree[now].ch[0]) now = tree[now].ch[0] ;
return now ;
}
void remove(int data)
{
int pre = query_pre(data) , suf = query_suf(data) ;
splay(pre , 0) ;
splay(suf , pre) ;
int del = tree[suf].ch[0] ;
if(tree[del].cnt > 1) tree[del].cnt-- , splay(del , 0) ;
else tree[suf].ch[0] = 0 ;
}
signed main()
{
insert(-inf) , insert(inf) ;
int n = read() ;
for(int opt , x , i = 1 ; i <= n ; i++)
{
opt = read() , x = read() ;
if(opt == 1) insert(x) ;
if(opt == 2) remove(x) ;
if(opt == 3) {Find(x) , printf("%lld\n" , tree[tree[root].ch[0]].sum) ;} ;
if(opt == 4) printf("%lld\n" , rank(x + 1)) ;
if(opt == 5) printf("%lld\n" , tree[query_pre(x)].val) ;
if(opt == 6) printf("%lld\n" , tree[query_suf(x)].val) ;
}
return 0 ;
}
FHQ - Treap
占个坑


 浙公网安备 33010602011771号
浙公网安备 33010602011771号