二分图
先言
今天讲师讲了二分图,貌似我以前真的没有学过,但是我发现真妙,所以我决定重新来梳理一下二分图的笔记
【定义】
二分图又称作二部图,是图论中的一种特殊模型。 设 \(G=(V,E)\) 是一个无向图,如果顶点 \(V\) 可分割为两个互不相交的子集 \((A,B)\) ,并且图中的每条边 \((i,j)\) 所关联的两个顶点 \(i\) 和 \(j\) 分别属于这两个不同的顶点集 \((i \in A , j \in B)\),则称图 \(G\) 为一个二分图。
以上来源于 360百科,具体什么意思,来个图解释一下。

我们假设左边的点是 \(A\) 集合, 右边的点形成 \(B\) 集合,然后二分图就相当于上方的那个图一样, 在 \(A\) 和 \(B\) 集合之中是没有连边的,连边只有在 \(A\) 和 \(B\) 两个集合相接的区域。
二分图最大匹配
给定一个二分图,其左部点的个数为 \(n\),右部点的个数为 \(m\),边数为 \(e\),求其最大匹配的边数。
我们称集合 \(A\) 和 \(B\) 之间的连边叫做匹配。就是有连边的意思
这里用的是匈牙利算法
匈牙利算法
【本质】 : 匈牙利算法的本质就是一个暴力,建立在二分图上的一个暴力,当模拟他的流程之后,就发现他真的是个暴力,但是这个暴力不同于我们普通的暴力。
我们同样以上述的图进行模拟匈牙利算法。
首先是 \(1\) 号节点开始扩展 ,我们扩展到 \(2\) 号节点 。 然后我们发现 \(2\) 号节点没被匹配,那么我们就可以让 \(1\) 号节点和 \(2\) 号节点匹配了,也就是下图

继续让 \(3\) 号扩展 ,我们扩展到 \(4\) 号节点,我们同样发现 \(4\) 号节点没有被匹配过,那么我们自然也可以让 \(3\) 号节点与 \(4\) 号节点匹配了。 如图所示
我们只要让 \(A\) 集合里的元素扩展即可
\(1,3\) 都已经匹配完成了,所以我们继续让 \(5\) 号节点匹配,\(5\) 号节点,能够继续与 \(6\) 号节点匹配,同理,下图 :
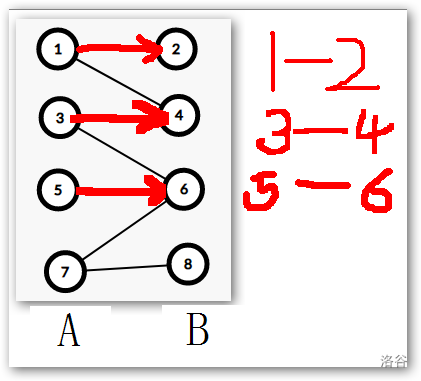
以下步骤请结合后文食用
那么继续扩展 \(7\) 号节点 ,我们首先会匹配 \(6\) 号节点,发现 \(6\) 号节点已经被别的节点匹配了,这个时候我们做的不是让 \(7\) 号节点寻找别的节点而是,废除 \(5\) 号节点与 \(6\) 号节点之间的匹配,让 \(7\) 号节点与 \(6\) 号节点匹配。
注 : 要是图实在是令你难以下咽,请转为文字吧
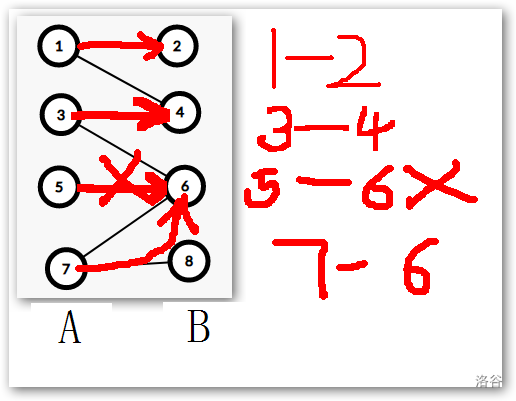
\(5\) 号节点继续扩展, 我们又找到了 \(6\) 号节点, 发现 \(6\) 号节点已经和 \(7\) 号节点匹配了,所以我们继续执行上一步的操作,将 \(7\) 号节点另寻别路了,所以废除 \(6\) 号节点和 \(7\) 号节点之间的匹配关系,我们选择让 \(5\) 号节点和 \(6\) 号节点匹配,让 \(7\) 号节点与 \(8\) 号节点建立匹配关系,然后就 \(Over!\)
Notice:
上述的两个步骤在匈牙利算法中并不是这么实现的,匈牙利算法是判断一下 \(6\) 号节点与 \(5\) 号节点废除匹配关系后, \(5\) 号节点是否可以找到一个新的匹配,如果可以,那么就废除 \(5\) 号和 \(6\) 号节点之间的匹配关系,如果不能找到一个 \(5\) 号节点可以匹配的关系,我们就不能废除 \(5\) 号节点与 \(6\) 号节点的匹配关系,而是让 \(7\) 号节点自己向下去找。上述的步骤是为了更好的理解。
杂 :
$YJK : $ 为什么 \(5\) 不能扩展到 \(8\) 号节点
$zzg : $ 因为没有连边
$YJK : $ 我傻了
\(Code\) :
实现就是分为两种,一种就是枚举 \(A\) 集合 \(B\) 集合,建立匹配关系, 然后再有一个 $bool $ 的 \(DFS\) 来判断一下废除节点的匹配关系是否可行,也就是废除上方 \(5\) 和 \(6\) 节点的匹配关系是否可行 。
具体代码如下 : 附有注释 :
/*
by : Zmonarch
知识点 :二分图最大匹配
匈牙利算法
*/
#include <iostream>
#include <cstring>
#include <cstdio>
#include <algorithm>
#include <queue>
#include <stack>
#include <map>
#include <set>
#include <vector>
#include <cmath>
#define int long long
const int kmaxn = 1e3 + 10 ;
inline int read()
{
int x = 0 , f = 1 ; char ch = getchar() ;
while(!isdigit(ch)) { if(ch == '-') f = - 1 ; ch = getchar() ; }
while( isdigit(ch)) { x = x * 10 + ch - '0' ; ch = getchar() ; }
return x * f ;
}
inline int Min(int a , int b)
{
if(a < b) return a ; else return b ;
}
inline int Max(int a , int b)
{
if(a > b) return a ; else return b ;
}
inline int Abs(int a )
{
if(a < 0) return - a ; else return a ;
}
int n , m , E ;
bool match[kmaxn][kmaxn] ; //表示 i ,j 之间有连边
bool used[kmaxn] ;
int ans ;
int nxt[kmaxn] ; // = j 表示 与 i 号节点相连的 j 号节点
bool dfs(int u)
{
for(int i = 1 ; i <= m ; i++)
{
if(match[u][i]) //首先要确定有边才可以进行扩展
{
if(used[i]) continue ;//边不能重复用
used[i] = 1 ;
if(!nxt[i] || dfs(nxt[i])) //如果 i 节点没有被匹配或者废除匹配关系也可以
{
nxt[i] = u ; //i与 u 相匹配
return true ;
}
}
}
return false ;
}
void match_()
{
for(int i = 1 ; i <= n ; i++)
{
memset(used , 0 , sizeof(used)) ;
if(dfs(i))
{
ans++ ;
}
}
}
signed main()
{
n = read() , m = read() , E = read() ;
for(int i = 1 ; i <= E ; i++)
{
int u = read() , v = read() ;
match[u][v] = 1 ;
}
match_() ;
printf("%lld\n" , ans) ;
return 0 ;
}
其他题目
经典题
草 ,没有link,这就很气。唔,那就不写代码了
【\(description\)】 :
给定 \(N\times N\) 矩阵,其中由\(1,0\)组成,矩阵可以自由交换行和列,问是否能使得如下图所示的对角线上的数全部都为 \(1\)
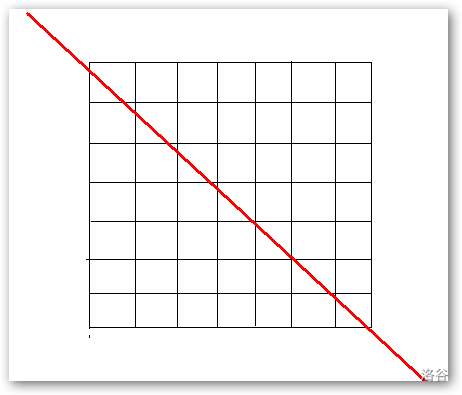
【\(solution\)】:
首先我们考虑我们在进行 行列交换的时候,如果某一列或者某一行中存在两个或者以上的 \(1\) ,我们需要考虑吗 ? 答案自然是不是, 在进行 行和列交换,无论怎么交换,一行和一列的 \(1\) 的个数自然是不会变的 ,我们做的是考虑一下是否能构成一个对角线 ,我们考虑用二分图来求解 。
那什么是左边的集合 \(A\)呢 ? 什么是右边的集合 \(B\) 呢? 答案其实也很显然,我们选择 列作为左边的集合, 将 行作为 右边的集合, 我们就可以得到一个二分图, 我们二分图的最大匹配只要是 \(n\) 答案就为 \(Yes\) , 不是就为 \(NO\) 。为什么是 \(n\) ,在一行或者一列中 \(1\)的位置自然是可以随意调换的 ,所以我们在进行匹配满足上述对角线的时候 ,我们需要满足上方对角线的点能够一一对应, 所以我们只要判断一下是否最大匹配数为 \(n\) 即可 。
杂 :
$YJK : $ 为什么最大匹配数不能大于 \(n\) ?
$zzg : $ 你的对角线的横坐标和纵坐标哪一个能大于 \(n\)
$YJK : $ 我傻了


 浙公网安备 33010602011771号
浙公网安备 33010602011771号