2 - SAT 问题
【定义】:
\(SAT\) 是适定性 \((Satisfiability)\) 问题的简称 。一般形式为 \(k\) -适定性问题,简称 \(k-SAT\)
这个描述来自于百度,没什么意义,主要是下面的概念
【问题描述】 :
\(k-SAT\) 的问题描述如下 :
一般有 \(x_1 , x_2 , x_3 …… x_n\) 等 \(n\) 个变量和 \(m\) 个关于 \(n\) 个变量之间的限制
每一个限制都是一个二元方程组, \(x_1 \bigoplus x_2 \bigoplus x_3 \bigoplus …… \bigoplus x_v = 0 / 1\) ,其中 \(\bigoplus\) 为一个二元 \(bool\) 形运算。
可以证明 \(k > 2\) 时,属于 \(NP\) 完全问题,只能用暴力解决, 本文讨论 \(2-SAT\) 问题。(可以认为笔者很是 \(fw\) ),连暴力也不知道怎么打。
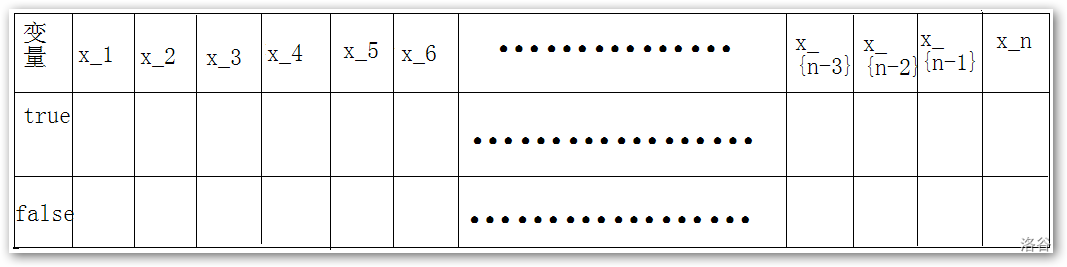
同样的,每一个变量大概就是这么一个图。
对于我来说, \(2-SAT\) 问题就是由 \(m\) 个约束条件形成的一张图。
【解决】 :
$2 - SAT $ 问题可以和图论相联系起来。 那么考虑建图
以一个例题作为简要讨论。
【模板】
【\(description\)】 :
见题面 。
【\(solution\)】:
我们以样例分析入手 。
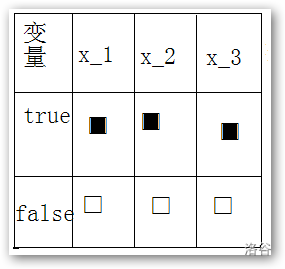
然后我们就可以建立出样例三个变量的图形了,有关图好看与否这种弱智讨论还是放一下吧
虽然这一个题目只有一个限制,但是说起来很好说 , 但是也是可以推导出一些东西的。
这一个限制是要么\(x_1 = 1\) ,要么\(x_3= 0\) ,这两个之间显然是必然有一个成立的。 或者说,至少有一个成立。对于\(x_3 \neq 0\),这个问题,我们是没有办法说是当\(x_1 = 1\) 时,\(x_3 \neq 0\) 一定成立。
关于这个问题的证明,倒是没那么好证,但是对于举出一个反例是相当的简单。如果有两个此时再有一个限制 , 要么\(x_3 = 0\),要么\(x_2 = 3\) ,那么这时候,这个\(x_3 = 0\)亦然是可能出现的。
所以我们也可以知道,关于上方的式子 :
当然,是个人都会知道\(\to\) 是推导的意思。 那么同样的,我们将推导和被推导出建边,~
同样的,点我们是需要建立两个的,分别代表\(true\) 和$false $ , 然后就没什么可说的了。
但是我们这个点是 \(true\) 的时候好记,但是当这一个是 \(false\) 的时候, 我们自然不能在\(1\to n\) 这些节点建立了,所以我们只能重新建立节点 ,那么我们这个节点数就往后顺延\(n\) , 举个例子,就是 \(1\) 的节点的对立面我们就新建结点 \(n+1\) 表示他的对立面。同样的,不同的题目用不同的方法,这个题自然是这么建好一些 的 。
由于这个题给定的就是真或者是假,那么我们就需要考虑一下
我们首先假设两个事件分别为 \(A\) 和事件 \(B\) ,
\(1.\) 那么当 \(A\) 假 \(and\) \(B\) 真的时候 ,那么我们就可以推导出 \(A\) 为真的时候,可以推导出 \(B\) 也是真的 , \(B\) 为假的时候 , \(A\) 也是为假
\(2.\) 当 \(A\) 假 \(and\) \(B\) 假的时候, 那么我们就可以推导出 \(A\) 为真的时候, \(B\) 为假,当 \(B\) 为真的时候, \(A\) 也是假
\(3.\) 当 \(A\) 真 \(and\) \(B\) 假的时候, 我们就可以推导出 \(A\) 为假的时候 , \(B\) 为假。
同理,当 \(B\) 为真的时候 ,\(A\) 为假 。
\(4.\) 当 \(A\) 真, \(B\) 真的时候, 我们同样可以推导出 \(A\) 为假的时候 , \(B\) 为真 ,
\(B\) 为假的时候 , \(A\) 为真
那么我们就可以得到建图的代码 :
for(int i = 1 ; i <= m ; i++ )
{
int x = read() , a = read() , y = read() , b = read() ;
if(a && b ) add(x , y + n) , add(y , x + n) ;
else if(!a && b) add(x + n , y + n) , add(y , x) ;
else if(a && !b) add(x , y) , add(y + n , x + n) ;
else if(!a && !b) add(x + n , y) , add(y + n , x ) ;
}
然后我们考虑什么时候会没有解,那必然是其对立面反而推出了自己,也就是节点 \(u\) 能够 被 \(u + n\) 这一个节点推导出来,这叫数学的反证法,如果不知道其具体,百度是个好东西,那么也就是说明, \(u\) 这一个节点和 \(u+n\) 这一个节点在一个强连通分量里。
同样的输出方案也就是强连通分量了,这里就不赘述强连通分量了。没有什么意义,若是不会的话,就看一下笔者曾经写过的一篇文章,\(Tarjan\) 算法
直接上代码 \(Code\)
/*
by : Zmonarch
知识点 :2 - SAT 模板
*/
#include <iostream>
#include <cstring>
#include <cstdio>
#include <algorithm>
#include <queue>
#include <stack>
#include <map>
#include <set>
#include <vector>
#include <cmath>
#define int long long
const int kmaxn = 2e6 + 10 ;
inline int read()
{
int x = 0 , f = 1 ; char ch = getchar() ;
while(!isdigit(ch)) { if(ch == '-') f = - 1 ; ch = getchar() ; }
while( isdigit(ch)) { x = x * 10 + ch - '0' ; ch = getchar() ; }
return x * f ;
}
inline int Min(int a , int b)
{
if(a < b) return a ; else return b ;
}
inline int Max(int a , int b)
{
if(a > b) return a ; else return b ;
}
inline int Abs(int a)
{
if(a < 0) return - a ; else return a ;
}
struct node
{
int nxt , u , v , val ;
} e[kmaxn << 1] ;
int n , m ;
int tot , h[kmaxn << 1] ;
void add(int u , int v )
{
e[++tot].nxt = h[u] ;
e[tot].u = u ;
e[tot].v = v ;
h[u] = tot ;
}
int dfn[kmaxn] , low[kmaxn] , stack[kmaxn] , in[kmaxn] , scc[kmaxn] ;
int top , sum , cnt ;
void Tarjan(int u)
{
dfn[u] = low[u] = ++sum ;
stack[++top] = u ;
for(int i = h[u] ; i ; i = e[i].nxt)
{
int v = e[i].v ;
if(!dfn[v])
{
Tarjan(v) ;
low[u] = Min (low[u] , low[v]) ;
}
else if(!in[v]) low[u] = Min (low[u] , dfn[v]) ;
}
if(low[u] == dfn[u])
{
in[u] = ++ cnt ;
++scc[cnt] ;
while(stack[top + 1] != u)
{
in[stack[top]] = cnt ;
++scc[cnt] ;
top -- ;
}
}
}
signed main()
{
n = read() , m = read() ;
for(int i = 1 ; i <= m ; i++ )
{
int x = read() , a = read() , y = read() , b = read() ;
if(a && b ) add(x , y + n) , add(y , x + n) ;
else if(!a && b) add(x + n , y + n) , add(y , x) ;
else if(a && !b) add(x , y) , add(y + n , x + n) ;
else if(!a && !b) add(x + n , y) , add(y + n , x ) ;
}
for(int i = 1 ; i <= n + n ; i++) //对立面也要搞
{
if(!dfn[i])
{
Tarjan(i) ;
}
}
for(int i = 1 ; i <= n ; i++ )
{
if(in[i] == in[i + n])
{
printf("IMPOSSIBLE\n") ;
return 0 ;
}
}
printf("POSSIBLE\n") ;
for(int i = 1 ; i <= n ; i++)
{
printf("%d " , in[i] > in[i + n] ) ;
}
return 0 ;
}
洛谷上的题就不再赘述了。
附加题
给定 \(n\) 个变量 ,为 \(x_1 , x_2 , x_3 , x_4 , x_5 , …… x_{n-1} , x_n\) \((\forall x \leq 100)\) , \(m\) 个表达式 , \(n , m \leq 100\)
有关表达式的形式 :
输入 \(4\) 个整数 , \(x_i , opt , x_j , val\) 。
意为 $$x_i + or \times or \div or - x_j \leq val$$
也就是加减乘除均可以。
那么考虑 \(2-SAT\) , 我们以 \(+\) ,为例,为什么用 \(+\) ,显然,好算,好说 。
我们给定一个式子 \(x_1 + x_2 \leq 5\)
如果我们选择以 \(x\) 的取值范围作为事件,那么我们就可以得到 \(true\) ,或者 \(false\) 了 ,就类似于上方的图,但是我并不打算用上方的图说明,笔者不怎么会用


 浙公网安备 33010602011771号
浙公网安备 33010602011771号