莫队
先言
来一写一下莫队,最近 \(YJK\) 一直在给我拍砖,导致我和一个 \(SB\) 一样,我决定写一篇找不出毛病的博文。
普通莫队: 算法简介
算的上是一个暴力美学,排序加分块,所以准确的来说,会了分块的思想和 \(sort\) 一些基础知识,你就可以手玩莫队了。莫队解决的是离线区间问题。 下方的图片:

我们就可以得到 \(a,b,c\) 三个查询区间,那么我们按照左端点进行排序,我们就可以得到 \(a,b,c\) 三个查询区间整齐的排列的区间上,我们暂且先不管右端点如何,我们暂且只管左端点。
我们假设两个头尾指针 \(l,r\) ,我们从左往右走,在走到第 \(a\) 号区间,我们 \(l = 1\) 显然已经到了我们要求的区间了,那么我们可以让 \(r\) 去蹦了,一直蹦到 \(n-4\) 也就是我们 \(a\) 号区间的右端点,统计完答案,然后我们再让 \(l ++\) 去寻找,我们就找到了 \(c\) 号查询区间,那么我们还是让 \(r\) 去找,同时我们看一下到底 \(c.r\) 和 \(r\) 的大小,然后让 \(r\) 逐步去接近它,最终得出答案。
最后就统计答案就行了 。
这就是普通莫队的流程了。
\(l\) 和 \(r\) 的区间移动

卡莫队
- 数字表示区间的左右端点
我们很显然的发现,如果按照我们这个回路的我们让 \(1\) 连 \(n\) ,让 \(2\to 3\) 让 \(3 \to n\) 一直这么下去,很显然,我们发现这货是 \(O(n^2)\) 的。这个这个莫队的算法限制
优化
我这个 \(fw\) 只有两种优化方式
- 1.\(register ,inline\) 并且把 \(add, del\) 操作给写到主函数里面去。可以能会优化 \(1S\) ,
- 2.奇偶排序 : 我们按照其左端点所在的块进行排序。\(li\) 表示的是 \(l\) 所在的块
inline bool cmp1(Block a , Block b) {return a.li == b.li ? a.l < b.l : a.r < b.r ; }
普通莫队:例题 :小Z的袜子
我们把它当模板,它没把自己当模板,它把莫队卡了,草
【description】:
求一个区间内每种颜色数目的平方和。
【solution】:
我们按照上述普通莫队的算法流程进行计算,我们同时我们开一个 \(cnt\) 记录一下当前的颜色数即可。 然后我们定义一个 \(ret\) 保证全局变量统计答案。
Code
没有办法 \(AC\) 我只有70分,写丑了
/*
by : Zmonarch
知识点 : 莫队
话说袜子分左右吗?
*/
#include <iostream>
#include <cstdio>
#include <cstring>
#include <algorithm>
#include <queue>
#include <stack>
#include <map>
#include <set>
#include <cmath>
#include <vector>
#define int long long
#define inf 63
#define re register
const int kmaxn = 1e6 + 10 ;
const int kmod = 1e9 + 7 ;
namespace Base
{
inline int Min(int a , int b) {return a < b ? a : b ; }
inline int Max(int a , int b) {return a > b ? a : b ; }
inline int Abs(int a ) {return a < 0 ? - a : a ; }
inline int gcd(int a , int b) {return !b ? a : gcd(b , a %b) ; }
}
inline int read()
{
int x = 0 , f = 1 ; char ch = getchar() ;
while(!isdigit(ch)) {if(ch == '-') f = - 1 ; ch = getchar() ; }
while( isdigit(ch)) {x = x * 10 + ch - '0' ; ch = getchar() ; }
return x * f ;
}
int num[kmaxn] , n , m , len , cnt[kmaxn] , l , r , ret ;
struct Block
{
int l , r , ans1 , ans2 , li , pos ;
}block[kmaxn] ;
inline bool cmp1(Block a , Block b)
{
return a.li == b.li ? a.l < b.l : a.r < b.r ;
}
inline bool cmp2(Block a , Block b)
{
return a.pos < b.pos ;
}
inline void add(int pos)
{
ret -= cnt[num[pos]] * cnt[num[pos]] ;
cnt[num[pos]]++;
ret += cnt[num[pos]] * cnt[num[pos]] ;
}
inline void del(int pos)
{
ret -= cnt[num[pos]] * cnt[num[pos]] ;
cnt[num[pos]]-- ;
ret += cnt[num[pos]] * cnt[num[pos]] ;
}
signed main()
{
n = read() , m = read() ; len = pow(n , 2/3) ;
for(re int i = 1 ; i <= n ; i++) num[i] = read() ;
for(re int i = 1 ; i <= m ; i++)
{
block[i].l = read() , block[i].r = read() ;
block[i].pos = i ; block[i].li = l / len ;
}
std::sort(block + 1 , block + m + 1 , cmp1) ;
l = 1 , r = 0 ;
for(re int i = 1 ; i <= m ; i++)
{
while(l < block[i].l) del(l++) ;
while(l > block[i].l) add(--l) ;
while(r < block[i].r) add(++r) ;
while(r > block[i].r) del(r--) ;
if(l == r)
{
block[i].ans1 = 0 ;
block[i].ans2 = 1 ;
continue ;
}
block[i].ans1 = ret - (r - l + 1 ) ;
block[i].ans2 = ( r - l + 1 ) * ( r - l ) ;
int g = Base::gcd(block[i].ans1 , block[i].ans2) ;
block[i].ans1 = block[i].ans1 / g ;
block[i].ans2 = block[i].ans2 / g ;
}
std::sort(block + 1 , block + m + 1 , cmp2) ;//最简
for(re int i = 1 ; i <= m ; i++) printf("%lld/%lld\n" , block[i].ans1 , block[i].ans2 ) ;
return 0 ;
}
普通莫队:题单
SP3267 DQUERY - D-query
P2709 小B的询问
P1494 [国家集训队]小Z的袜子
P3709 大爷的字符串题
CF617E XOR and Favorite Number
带修莫队:算法简介 :
在普通莫队的基础上,我们推出了带修莫队,也就是带修改的莫队。
现在我们需要对区间进行修改,如果我们重新打乱,进行修改(首先这是在线,不怎么可取) ,我们直接记录 \(last\) 表示在这个时间内最近一次修改。
我们假设现在需要查询的区间为 \(l\to r\) ,那么我们需要修改的 \(pos\) 和 \(l,r\) 有三种显然的关系
- \(pos < l < r\) ,这么说的话,我们根本不需要在意这次的修改
- \(l < r < pos\) ,同上
- \(l < pos < r\) 也就是说,我们在这次的区间访问中有将该区间的元素修改的操作(我们通过在时间轴上的 \(l , r\) 区间的访问时间和 \(query\) 访问区间的时间),然后我们直接修改,同时我们进行修改的时候,到了那个地方再修改。
结合代码更好理解一些
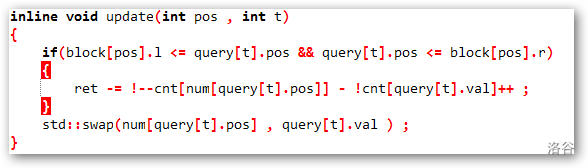

\(update\) 操作就是更修改操作。
- t 表示的是一个时间轴,我们把每一次修改操作都看成在 \(tot2\) 的时间内进行的一个 \(np\) 操作,然后我们将 \(t\) 赋值成最近的那一次, 然后我们在 \(update\) 的时候,进行一下判断,也就是看一下是否在这个区间内,然后进行一系列的操作,同时,因为修改了,所以讲你原来的值和修改的值换一换
例题:带修莫队:P1903数颜色
【description】:
给定两个操作,操作一是查询区间内有多少个不同的数字,操作二支持修改。
【solution】:
占个坑,我觉得我能写不少。
【Code】 :
/*
by : Zmonarch
知识点 : 带修莫队
*/
#include <iostream>
#include <cstdio>
#include <cstring>
#include <cmath>
#include <algorithm>
#include <queue>
#include <stack>
#include <set>
#include <map>
#include <vector>
#define int long long
#define inf 63
#define re register
const int kmaxn = 1e6 + 10 ;
const int kmod = 1e9 + 7 ;
namespace Base
{
inline int Min(int a , int b) {return a < b ? a : b ; }
inline int Max(int a , int b) {return a > b ? a : b ; }
inline int Abs(int a ) {return a < 0 ? - a : a ; }
inline int gcd(int a , int b) {return !b ? a : gcd(b , a %b) ; }
}
inline int read()
{
int x = 0 , f = 1 ; char ch = getchar() ;
while(!isdigit(ch)) {if(ch == '-') f = - 1 ; ch = getchar() ; }
while( isdigit(ch)) {x = x * 10 + ch - '0' ; ch = getchar() ; }
return x * f ;
}
int n , m , len ;
struct Block //记录询问
{
int l , r , t , pos , ans ;
}block[kmaxn << 1] ;
struct change //记录修改
{
int pos , val , id , t ;
}query[kmaxn << 1] ;
int num[kmaxn << 1] , ret , tot1 , tot2 , cnt[kmaxn << 1];
//tot1表示询问的区间,tot2表示询问
inline void add(int pos)
{
ret += (++cnt[num[pos]] == 1) ;
}
inline void del(int pos)
{
ret -= (--cnt[num[pos]] == 0) ;
}
inline bool cmp1(Block a , Block b)
{
return (a.l/len ^ b.l/len) ?a.l/len < b.l/len : ((a.r/len ^ b.r/len) ? a.r/len < b.r/len : a.t < b.t );
}
inline bool cmp2(Block a , Block b)
{
return a.pos < b.pos ;
}
inline void update(int pos , int t)
{
if(block[pos].l <= query[t].pos && query[t].pos <= block[pos].r)
{
ret -= !--cnt[num[query[t].pos]] - !cnt[query[t].val]++ ;
}
std::swap(num[query[t].pos] , query[t].val ) ;
}
signed main()
{
n = read() , m = read() ; len = pow(n , (double)2.0/3.0) ;
//dalao说n^1/2会退化成n^2
for(int i = 1 ; i <= n ; i++) num[i] = read() ;
for(int i = 1 ; i <= m ; i++)
{
char s[5] ; scanf("%s" , s ) ;
int l = read() , r = read() ;
if(s[0] == 'Q') ++tot1 , block[tot1].pos = tot1 , block[tot1].l = l , block[tot1].r = r , block[tot1].t = tot2 ;
if(s[0] == 'R') query[++tot2].pos = l , query[tot2].val = r ;
}
std::sort(block + 1 , block + tot1 + 1 , cmp1) ;
int l = 1 , r = 0 , t = 0 ;
for(int i = 1 ; i <= tot1 ; i++)
{
while(l > block[i].l) add(--l) ; //ret += !cnt[num[--l] ]++; //
while(l < block[i].l) del(l++) ; //ret -= !--cnt[num[l++]] ; //
while(r > block[i].r) del(r--) ;//ret -= !--cnt[num[r--]] ;//
while(r < block[i].r) add(++r) ;//ret += !cnt[num[++r]]++ ;//
while(t < block[i].t) update(i , ++t) ;
while(t > block[i].t) update(i , t--) ;
block[i].ans = ret ;
}
std::sort(block + 1 , block + tot1 + 1 , cmp2) ;
for(int i = 1 ; i <= tot1 ; i++) printf("%lld\n" , block[i].ans) ;
return 0 ;
}
带修莫队:题单
树上莫队:算法简介
我们如果学过树链剖分的话,我们就很显然的清楚,在一个树上,如果进行操作的话,我们会选择用树链剖分将整颗树剖下来。我们把树上剖下来的链看成区间,那么我们就有了莫队的资格。

以上述的图为例,我们看一下树上莫队。
首先我们先考虑不在同一颗子树内的时候,也就是是其中 \(f \to a\) 的简单路径,我们抽出来进行一下操作,我们搞出来的欧拉序中恰好从 \(a \to f\) 正好是我们要的结果,这可能是一种特例。
考虑在用一颗子树内的时候, 也就是其中 \(f\to e\) 的时候,我们继续寻找欧拉序,我们发现在 \(f\to e\) 的欧拉序中,如果出现两次一样的节点,那么这个点就绝不是简单路径 , \(f ,e\) 分别从第二个和第一个算起。(也就是没有重合的时候),这是欧拉序的性质使然,有兴趣的直接去查一下欧拉序吧。
我们发现其中没有 \(b\) 点,也就是没有 \(lca\) 这是什么原因? 在一个根节点为 \(now\) 的子树,它的子树的节点形成的欧拉序对于紧跟在 \(now\) 之后,并且在下一次 \(now\) 出现之前。
也就是 \(f\to e\) 这一条路径,因为全在 \(b\) 这一颗子树内,我们在欧拉序中是无法遍历到 \(b\) 这个点的,所以我们需要记录一下 \(lca\) 进行一下特判
树上莫队: 例题:SP10707 COT2 - Count on a tree II
【description】 :
占个坑,有空回来补,有些遗忘了
【Solution】:
Code :
/*
by : Zmonarch
知识点 :
*/
#include <iostream>
#include <cstdio>
#include <algorithm>
#include <cmath>
#include <queue>
#include <stack>
#include <set>
#include <cstring>
#include <map>
#include <cstdlib>
#define int long long
#define inf 2147483647
const int kmaxn = 1e6 + 10 ;
const int kmod = 1e9 + 7 ;
namespace base
{
inline int Min(int a , int b) { return a < b ? a : b ; } ;
inline int Max(int a , int b) { return a > b ? a : b ; } ;
inline int Abs(int a ) { return a < 0 ? - a : a ; } ;
};
inline int read()
{
int x = 0 , f = 1 ; char ch = getchar() ;
while(!isdigit(ch)) { if(ch == '-') f = - 1 ; ch = getchar() ; }
while( isdigit(ch)) { x = x * 10 + ch - '0' ; ch = getchar() ; }
return x * f ;
}
using namespace base ;
struct Block
{
int l , r , li , ri , ans , lca , pos ;
}block[kmaxn << 1] ;
int n , m , ret , sum , len ;
int f[kmaxn << 1] , dep[kmaxn << 1] , top[kmaxn << 1] , son[kmaxn << 1] , size[kmaxn << 1] , st[kmaxn << 1] ;
int ed[kmaxn << 1] , num[kmaxn << 1] , id[kmaxn << 1] , used[kmaxn << 1] , cnt[kmaxn << 1] , b[kmaxn << 1];
bool cmp1(Block a , Block b) //OK
{
return (a.li == b.li) ? (a.li & 1) ? a.r < b.r : a.r > b.r : a.l < b.l ;
}
bool cmp2(Block a , Block b)
{
return a.pos < b.pos ;
}
struct node
{
int nxt , u ,v , val ;
}e[kmaxn << 1] ;
int tot , h[kmaxn << 1] ;
void add(int u , int v)
{
e[++tot].nxt = h[u] ;
e[tot].u = u ;
e[tot].v = v ;
h[u] = tot ;
}
void add(int pos) //OK
{
ret += (++cnt[num[pos]] == 1) ;
}
void del(int pos) //ok
{
ret -= (--cnt[num[pos]] == 0) ;
}
void check(int pos) //检查一下是否应该在莫队中,也就是是否在同一条链上。 // OK
{
if(!used[pos]) add(pos) ;
else del(pos) ;
used[pos] ^= 1 ;
}
void dfs1(int u , int fa) //第一个DFS求解深度和子树大小和重儿子
{
f[u] = fa ;
st[u] = ++sum ; //记录入栈顺序
id[sum] = u ;
size[u] = 1 ;
dep[u] = dep[fa] + 1 ;
for(int i = h[u] ; i ; i = e[i].nxt)
{
int v = e[i].v ;
if(v == fa) continue ;
dfs1(v , u) ;
size[u] += size[v] ;
if(size[v] > size[son[u]]) son[u] = v ;
}
ed[u] = ++ sum ; id[sum] = u ; //记录出栈顺序,并且记录u的欧拉序
}
void dfs2(int u , int topp ) //剖链
{
top[u] = topp ;
if(son[u]) dfs2(son[u] , topp) ;
for(int i = h[u] ; i ; i = e[i].nxt )
{
int v = e[i].v ;
if(v == f[u] || v == son[u]) continue ;
dfs2(v , v) ;
}
}
int getlca(int u , int v)
{
while(top[u] != top[v])
{
if(dep[top[u]] >= dep[top[v]]) u = f[top[u]] ;
else v = f[top[v]] ;
}
return dep[u] < dep[v] ? u : v ;
}
signed main()
{
n = read() , m = read() ; len = sqrt(n) ;
for(int i = 1 ; i <= n ; i++) num[i] = read() , b[i] = num[i] ;
std::sort(b + 1 , b + n + 1) ;
for(int i = 1 ; i <= n ; i++)
num[i] = std::lower_bound(b + 1 , b + n + 1 , num[i]) - b ;
for(int i = 1 ; i <= n - 1 ; i++)
{
int u = read() , v = read() ;
add(u , v) , add(v , u) ;
}
dfs1(1 , 0) ;
/*for(int i = 1 ; i <= n ; i++) printf("test %lld %lld %lld\n" , st[i] , ed[i] , dep[i]) ; */
dfs2(1 , 1) ;
for(int i = 1 ; i <= m ; i++)
{
int u = read() , v = read() ; if(st[u] > st[v]) std::swap(u , v) ;
block[i].pos = i ; block[i].lca = getlca(u , v) ;
if(block[i].lca == u)
{
block[i].l = st[u] ;
block[i].r = st[v] ;
block[i].lca = 0 ; //后边需要特判一下没有遍历到LCA的情况
}
else
{
block[i].l = ed[u] ;
block[i].r = st[v] ;
}
block[i].li = block[i].l / len ;
block[i].ri = block[i].r / len ;
}
std::sort(block + 1 , block + m + 1 , cmp1) ;
int l = 1 , r = 0 ;
for(int i = 1 ; i <= m ; i++)
{
while(l < block[i].l) check(id[l++]) ;
while(l > block[i].l) check(id[--l]) ;
while(r < block[i].r) check(id[++r]) ;
while(r > block[i].r) check(id[r--]) ;
if(block[i].lca) check(block[i].lca) ;
block[i].ans = ret ;
// printf("ret : %lld\n" , ret) ;
if(block[i].lca) check(block[i].lca) ;
}
std::sort(block + 1 , block + m + 1 , cmp2) ;
for(int i = 1 ; i <= m ; i++) printf("%lld\n" , block[i].ans) ;
return 0 ;
}
题单:树上莫队
P4689 [Ynoi2016] 这是我自己的发明
P4074 [WC2013] 糖果公园
回滚莫队: 算法简介
首先我们按照区间左端点所在的块进行排序,同时按照 \(r\) 为第二关键字排序,然后我们就可以得到一个左端点漂浮不定,右端点递增,但整体看起开递增的一个不错的询问。
我们在进行操作的时候,普通没有什么两样,但是在进行查询区间的时候,我们利用分块的思想,我们看一下我们询问的区间是否是在一个块内,如果在一个块内的话, 我们就可以直接 \(O(\sqrt n)\) 的暴力进行求解,同时对于不是在用一个块内,我们先进行求解右端点,因为右端点是递增的,我们这次通过这个右端点求出答案对后面是有贡献的。但是我们这个左端点是一丢丢的贡献都没有,所以我们最后求解完成这个左节点,我们把答案归还,然后下一个区间的时候,在让他自己去向前找左端点。 这就叫做回 - 滚
回滚莫队:例题:[P5906 【模板】回滚莫队&不删除莫队
](https://www.luogu.com.cn/problem/P5906)
solution
和上述算法流程讲述一致 ,我们分别计入两个 \(ma ,st\) 表示头尾,然后正常的回滚莫队即可。
Code
/*
By : Zmonarch
知识点 :
*/
#include <iostream>
#include <cstdio>
#include <algorithm>
#include <cmath>
#include <queue>
#include <stack>
#include <cstring>
#include <vector>
#include <map>
#include <set>
#define int long long
#define inf 2147483647
#define qwq register
const int kmaxn = 1e6 + 10 ;
const int kmod = 998244353 ;
namespace Base
{
inline int Min(int a , int b) {return a < b ? a : b ;}
inline int Max(int a , int b) {return a < b ? b : a ;}
inline int Abs(int a) {return a < 0 ? - a : a ;}
inline int Gcd(int a , int b) {return !b ? a : Gcd(b , a % b) ;}
}
inline int read()
{
int x = 0 , f = 1 ; char ch = getchar() ;
while(!isdigit(ch)) {if(ch == '-') f = - 1 ; ch = getchar() ; }
while( isdigit(ch)) {x = x * 10 + ch - '0' ; ch = getchar() ; }
return x * f ;
}
int n , m , Max , len , ret ;
int num[kmaxn] , b[kmaxn] , cnt[kmaxn] , belong[kmaxn] , st[kmaxn] , ma[kmaxn] , clear[kmaxn];
struct Block
{
int l , r , id , ans ;
}block[kmaxn] ;
inline int calc(int l , int r)
{
static int tim[kmaxn] ; int ans = 0 ;
for(qwq int i = l ; i <= r ; i++) tim[num[i]] = 0 ;
for(qwq int i = l ; i <= r ; i++)
if(!tim[num[i]]) tim[num[i]] = i ;
else ans = Base::Max(ans , i - tim[num[i]]) ;
return ans ;
}
inline int work(int i , int id)
{
int R = Base::Min(n , id * len) , l = R + 1 , r = l - 1 ; ret = 0 ;
int sum = 0 ;
memset(cnt , 0 , sizeof(cnt)) ;
for(; belong[block[i].l] == id ; i++)
{
if(belong[block[i].l] == belong[block[i].r])
{block[i].ans = calc(block[i].l , block[i].r) ; continue ;}
while(r < block[i].r)
{
r++ ; ma[num[r]] = r ;
if(!st[num[r]]) st[num[r]] = r , clear[++sum] = num[r] ;
ret = Base::Max(ret , r - st[num[r]]) ;
}
int cur = ret ;
while(l > block[i].l)
{
l-- ;
if(ma[num[l]]) ret = Base::Max(ret , ma[num[l]] - l) ;
else ma[num[l]] = l ;
}
block[i].ans = ret ;
while(l <= R) {if(ma[num[l]] == l) ma[num[l]] = 0 ; l++;}
ret = cur ;
}
for(qwq int i = 1 ; i <= sum ; i++) ma[clear[i]] = st[clear[i]] = 0 ;
return i ;
}
inline bool cmp1(Block a , Block b) {return belong[a.l] ^ belong[b.l] ? belong[a.l] < belong[b.l] : a.r < b.r ;}
inline bool cmp2(Block a , Block b) {return a.id < b.id ;}
signed main()
{
n = read() ; len = sqrt(n) ;
for(qwq int i = 1 ; i <= n ; i++)
num[i] = read() , b[i] = num[i] , belong[i] = (i - 1) / len + 1 , Max = Base::Max(Max , belong[i]);
std::sort(b + 1 , b + n + 1) ;
int tot = std::unique(b + 1 , b + n + 1) - b - 1 ;
for(qwq int i = 1 ; i <= n ; i++) num[i] = std::lower_bound(b + 1 , b + tot + 1 , num[i]) - b ;
m = read() ;
for(qwq int i = 1 ; i <= m ; i++)
block[i].l = read() , block[i].r = read() , block[i].id = i ;
std::sort(block + 1 , block + m + 1 , cmp1) ;
for(qwq int i = 1 , id = 1 ; id <= Max ; id++) i = work(i , id) ;
std::sort(block + 1 , block + m + 1 , cmp2) ;
for(qwq int i = 1 ; i <= m ; i++) printf("%lld\n" , block[i].ans) ;
return 0 ;
}
题单:回滚莫队
AT1219 歴史の研究
P5386 [Cnoi2019]数字游戏
P6072 『MdOI R1』Path
写在最后
个人感觉莫队没有什么太大的说头,如有哪些地方不明白,还请直接让博主知道,予以补充,关于题解的话,都是洛谷上的题,题解就直接看那上面的吧,反正都是模板题(打的最后不一样就赖不着了),只讲一下流程应该就 \(OK\) 的。 本来不打算写代码,但是感觉太少了,就附上代码了。


