有关连通性
前序
本来整理过 \(Tarjan\) ,但是那一篇博客讲的不是很好,并且有好几处错误,最后决定重修,准确的说,那一篇是我写过最长的博客了。
你能够学到什么
- 强连通分量
- 双连通分量
- 割点和桥
一丢丢的概念
或许可以帮助理解后面的算法之类的,这里建议看一下,了解一下最好。
强连通分量
强连通分量的概念
值得注意的是,有向图
两个点能够互相到达,我们称其为强连通。
一张图 \(G\) 中的一张子图 \(G_1\) 满足 \(G_1\) 内的任意两个点可以互相到达,那么我们称 \(G_1\) 是 \(G\) 的一个强连通分量。
或许这么说也挺合适的 : 强连通分量就是图中的环。
DFS 生成树
在了解 \(Tarjan\) 算法之前,我们需要了解一下 \(DFS\) 生成树。
随手画了一个图,结果,哈哈,只有树边和一条返祖边,借用一下 OI-WiKi的图
感谢 OI - Wiki 的赞助。

来点定义 :
树边 : 就是搜索树上的边,略微解释一下,就是在搜索到一个没有被访问过的节点,就形成了一条树边。 就是图中绿色的那些条
返祖边 : 也叫作回边, 指向它祖先的边 , 就是图中黄色的那些条
横叉边 : 它主要是在搜索的时候遇到了一个已经访问过的结点,但是这个结点 并不是 当前结点的祖先时形成的 , 图中的红色边
前向边 : 指向搜索树子树的节点的边 , 就是图中蓝色的边
强连通分量和 DFS 生成树的关系
如果 \(u\) 是某一个强连通分量的在搜索中遇到的第一个节点,那么这一个强连通分量的其余所有的节点都在以 \(u\) 为根的搜索子树内。
证明:借鉴 OI - Wiki 反证法 。
如果存在一个节点 \(k\) 在强连通分量里,但是却不在以 \(u\) 为根的子树内,那么也就是说在 \(u\) 到 \(k\) 的路径中,必有一条边会离开这一棵子树,那么这一条边一定是返祖边或者横叉边,否则是出不去的。那返祖边和横叉边都有一个限制,就是要求指向的点被访问过了,如果这个点被访问过了,那么 \(u\) 也就是不是第一个节点了,和条件冲突,故成立。
Tarjan 算法求解
由于笔者不是 \(Tarjan\) 老爷爷,所以我们感性理解,通过代码去理解,笔者也也不清楚老爷爷是怎么想出来的。这里提供代码和算法举例说明。
我们先给定一些约定 :
\(dfn_u\) 表示深度优先搜索遍历时结点 \(u\) 被搜索的次序。
\(low_u\) : 设以 \(u\) 为根的子树为 \(sub(u)\) , \(low_u\) 定义为以下节点的 \(dfn\) 最小值 : \(sub(u)\) 中的所有节点,从 \(sub(u)\) 通过一条不在搜索树上的边能够到达的所有点。
\(h,e\) 表示的是链式前向星存图,相信应该都是没有问题的。
\(in_x\) 表示的\(x\)这一个节点隶属于哪一个连通块(也就是强连通分量)
\(stack\) 表示还没有划分成连通块的节点
\(scc\) 表示的联通块的大小
\(cnt\) 就表示总共有多少个联通块
\(top\) 显然就是栈顶
void tarjan(int u )
{
low[u] = dfn[u] = ++ sum ;
stack[++top] = u ;
for(int i = h[u] ; i ; i = e[i].nxt)
{
int v = e[i].v ;
if(!dfn[v])
{
tarjan(v) ;
low[u] = min (low[u] , low[v]) ;
}
else if(!in[v]) low[u] = min (low[u] , dfn[v]) ;
}
if(low[u] == dfn[u])
{
in[u] = ++ cnt ;
++scc[cnt] ;
while(stack[top + 1] != u )
{
++scc[cnt] ;
in[stack[top]] = cnt ;
top -- ;
}
}
}
然后结合一下图来说明:
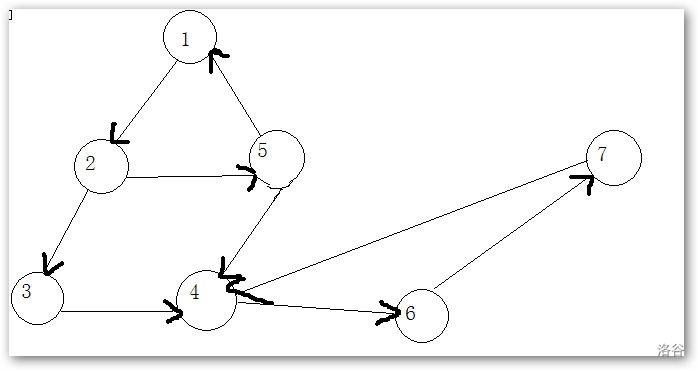
很显然,通过上帝视角,我们发现,其中的强连通分量是(我们用集合来表示一下)
\((1 \to 2 \to5) , (4\to 6 \to 7) , 3\)这三个连通分量, 同样的,我们来手动模拟一下\(Tarjan\)算法的这个过程
首先,我们是进行了\(DFS\),搜索(为了简述方便,我们规定这一个搜索的顺序是从左到右的) ,就可以得到这么一个手动模拟的过程

之后我们发现,再次从\(7\)这一个点,出发的时候,我们找到\(4\)这一个点,同时,也是在存储的时候我们也发现\(4\)这一个点已经在\(stack\)中了,所以我们也很容易理解,从\(4 \to 7\)这一个过程经历的必然是一个强连通分量(或者说,是一个环),相应的,很好理解, 如果我们不用\(low\)记录一下这个最小值,我们根本不知道这一个环是从什么时候开始的,所以\(low\)的重要性,也就可以体现了,我们找完了一个\((4 \to 6 \to 7)\)这一个环

这里写一个代码,更深刻的理解一下,当找到一个环的时候,也就是我们的这个\(low\)的最小值和下一次搜索出来的是一样的时候,我们把栈中\(low\)之后的全部弹出去,就记录了\(scc_i\)(第\(i\)个连通分量的大小了) ,当然当求解\((3)\)这一个连通分量也是一样的道理。
继续看一下求解\((1 \to 2 \to 5)\)这一个连通分量
我们划去已经匹配了的节点,此时的$stack : 1 , 2 $还是给图吧
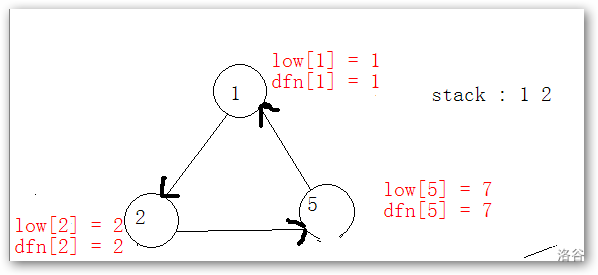
我们继续寻找,略过找到\(5\)这个节点,我们还是发现,又回到原点了, 同上述的\((4 \to 6 \to 7)\)这一个环,就行了。
具体处理
我们已经处理完了 \(u\) , 将要处理 \(u\) 指向的点 \(v\)
-
当 \(v\) 没有被访问过,那么我们就继续 dfs , 令 \(low_u\)成为其连接的直接路径的 dfn 中最小的。
-
当 \(v\) 被访问过了,但是还在栈中,那么我们就用 \(dfn_v\) 来更新 \(low_u\) , 使其成为 \(sub(u)\) 中最小的 。
-
当 \(v\) 被访问过了,也不在栈中,那么我们就直接不用管了,它已经处理完了。
关于强连通分量的操作,就直接搞,往里面塞就行了。
题目 :
B3609 [图论与代数结构 701] 强连通分量
P2341 [USACO03FALL][HAOI2006]受欢迎的牛 G
割点和桥
这些为无向图中的。
割点 :
对于一个无向图,如果把一个点删掉以后这个图的极大连通分量数增加了,则该点为割点。
其实也就是该点影响了该图的连通性。
图解割点
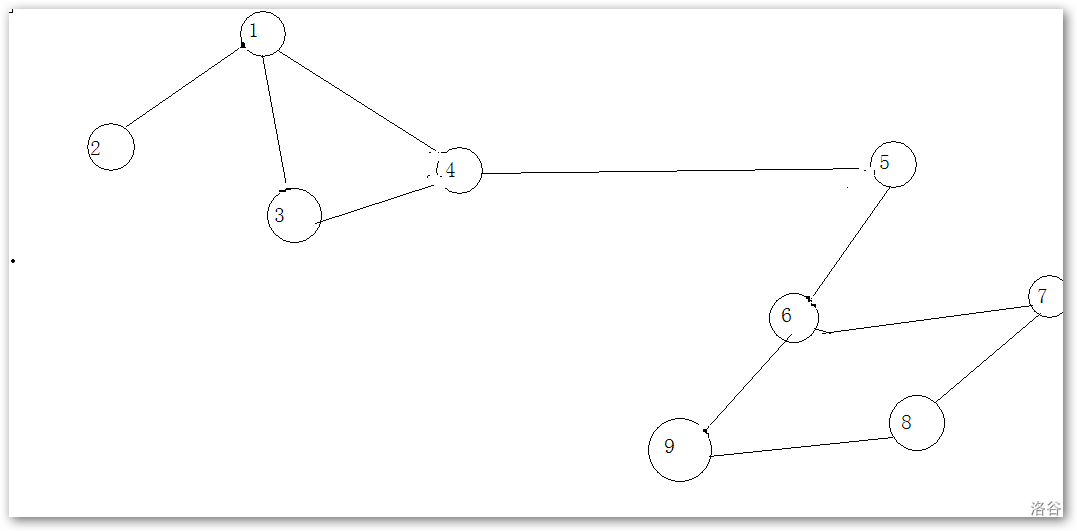
该图中,我们枚举删除判断过程
我们删去\(2\)这个节点,连通块不变,还是1个
删去\(1\)这个节点,连通块变为\(2\)个,所以\(1\)是一个割点
删去\(3\)这个节点,连通块不变,仍为\(1\)个,所以\(3\)不是割点
删去\(4\)这个节点,连通块变为\(2\)个,所以\(4\)是割点
删去\(5\)这个节点,连通块变为\(2\)个,所以\(5\)是割点
删去\(6\)这个节点,连通块变为\(2\)个,所以\(6\)是割点
删去\(7\)这个节点,连通块不变,仍为\(1\)个,所以\(7\)不是割点
删去\(8\)这个节点,连通块不变,仍为\(1\)个,所以\(8\)不是割点
删去\(9\)这个节点,连通块不变,仍为\(1\)个,所以\(9\)不是割点
综上, \(1,4,5,6\)是割点 。
求解模拟割点
我们首先就是有一个非常暴力的但是有效的解决办法 : 枚举删除每一个点,再 \(DFS\) 判断一下连通性,看一下是否连通分量增加了。 不过这个的复杂度不能够承受。
丢一个定理 : 割点判定定理
如果在搜索树上有节点 \(u\) 和其子节点 \(v\) 满足 \(dfn_u \leq low_v\) , 则 \(u\) 为割点。特别的,当\(x\)是搜索树的根时,则 \(x\) 为割点当且仅当搜索树上存在至少两个子节点 \(v_1 , v_2\) 满足上述条件。
\(low , dfn\) 的定义和上述一致。
证明 : 不知。 略。
模板题 : P3388 【模板】割点(割顶)
//
/*
Author : Zmonarch
Knowledge :
*/
#include <bits/stdc++.h>
#define inf 2147483647
#define qwq register
#define qaq inline
#define int long long
using namespace std ;
const int kmaxn = 1e6 + 10 ;
qaq int read() {
int x = 0 , f = 1 ; char ch = getchar() ;
while(!isdigit(ch)) {if(ch == '-') f = - 1 ; ch = getchar() ;}
while( isdigit(ch)) {x = x * 10 + ch - '0' ; ch = getchar() ;}
return x * f ;
}
int n , m , tot , cnt , num ;
struct node {
int nxt , u , v ;
}e[kmaxn << 1];
int h[kmaxn] , dfn[kmaxn] , low[kmaxn];
bool f[kmaxn] ;
qaq void add(int u , int v) {
e[++tot].nxt = h[u] ;
e[tot].u = u ; e[tot].v = v ;
h[u] = tot ;
}
qaq void Tarjan(int u , int fa) {
int child = 0 ; low[u] = dfn[u] = ++ cnt ;
for(qwq int i = h[u] ; i ; i = e[i].nxt)
{
int v = e[i].v ;
if(!dfn[v])
{
Tarjan(v , u) ;
low[u] = min(low[u] , low[v]) ;
if(u != fa && low[v] >= dfn[u]) f[u] = 1 ;
if(u == fa) child++ ;
}
low[u] = min(low[u] , dfn[v]) ;
}
if(child >= 2 && u == fa) f[u] = 1 ;
}
signed main() {
n = read() , m = read() ;
for(qwq int i = 1 ; i <= m ; i++)
{
int u = read() , v = read() ;
add(u , v) ; add(v , u) ;
}
for(qwq int i = 1 ; i <= n ; i++)
if(!dfn[i]) Tarjan(i , i) ;
for(qwq int i = 1 ; i <= n ; i++)
if(f[i]) num++ ;
printf("%lld\n" , num) ;
for(qwq int i = 1 ; i <= n ; i++)
if(f[i]) printf("%lld " , i) ;
return 0 ;
}
桥 , 割边
桥和割边的定义为 : 在图中删去一条边,其连通分量的数目增加,该边即为割边。
图解模拟割边

我们手模枚举删除边
删去\(1\)号边,连通块变为\(2\)个,所以,\(1\)号是割边
删去\(2\)号边,连通块不变,所以,\(2\)号不是割边
删去\(3\)号边,连通块不变,所以,\(3\)号不是割边
删去\(4\)号边,连通块不变,所以,\(4\)号是割边
删去\(5\)号边,连通块变为\(2\)个,所以,\(5\)号是割边
删去\(6\)号边,连通块变为\(2\)个,所以,\(6\)号是割边
删去\(7\)号边,连通块不变,所以,\(7\)号不是割边
删去\(8\)号边,连通块不变,所以,\(8\)号不是割边
删去\(9\)号边,连通块不变,所以,\(9\)号不是割边
还有一条忘记标号的边,不过和 \(7,8,9\) 号边是一样的。
综上所述,\(1,5,6\)是割边,其余的都不是割边
求解割边
再丢一个定理 :
如果 \((u , v)\) 为桥,当且仅当搜索树上存在 \(u\) 的一个子节点 \(v\) , 满足 \(dfn_u < low_v\)
证明:不知 。
准确的来说,所有给定的证明在我看来都是感性理解。没有任何严谨的证明,故不清楚其证明过程。紫书的证明感性理解带师。
大致和割点是一样的,但是某些地方是不一样的。
- \(1.\) 割点是 \(dfn_u \leq low_v\) 并且需要考虑一下 \(u\) 为根的时候,但是割边为 \(dfn_u < low_v\) 并且无需考虑 \(u\) 为根的情况。
- 但是要注意的就是这个图是无向图,在进行 \(Tarjan\) 操作的时候,我们不能去更新其父亲节点,所以我们用 \(fa\) 去记录一下节点 \(u\) 的父亲节点,判断一下就行了。
大佬造了 数据 T103481 【模板】割边
求解所有的割边的数目。
//
/*
Author : Zmonarch
Knowledge :
*/
#include <bits/stdc++.h>
#define inf 2147483647
#define qwq register
#define qaq inline
#define int long long
using namespace std ;
const int kmaxn = 1e6 + 10 ;
qaq int read() {
int x = 0 , f = 1 ; char ch = getchar() ;
while(!isdigit(ch)) {if(ch == '-') f = - 1 ; ch = getchar() ;}
while( isdigit(ch)) {x = x * 10 + ch - '0' ; ch = getchar() ;}
return x * f ;
}
int n , m , sum , cnt , tot = 1 , ans ;
struct node {
int nxt , u , v ;
}e[kmaxn << 1];
int dfn[kmaxn] , low[kmaxn], h[kmaxn] ;
bool f[kmaxn] ;
qaq void add(int u , int v) {
e[++tot].nxt = h[u] ;
e[tot].u = u ; e[tot].v = v ;
h[u] = tot ;
}
qaq void Tarjan(int u , int fa) {
dfn[u] = low[u] = ++ sum ;
for(qwq int i = h[u] ; i ; i = e[i].nxt)
{
int v = e[i].v ;
if(!dfn[v])
{
Tarjan(v , u) ;
low[u] = min(low[u] , low[v]) ;
if(dfn[u] < low[v]) f[i] = f[i ^ 1] = true ;
}
else if(v != fa) low[u] = min(low[u] , dfn[v]) ;
}
}
signed main() {
n = read() , m = read() ;
for(qwq int i = 1 ; i <= m ; i++)
{
int u = read() , v = read() ;
add(u , v) ; add(v , u) ;
}
for(qwq int i = 1 ; i <= n ; i++)
if(!dfn[i]) Tarjan(i , i) ;
for(qwq int i = 1 ; i <= tot ; i += 2 )
if(f[i]) ans++ ;
printf("%lld\n" , ans) ;
return 0 ;
}
双连通分量
分为点双连通分量和边双连通分量
因为边双和点双的相似度十分高,所以笔者这里很多地方将点双和边双放在一起了,不会有很明显的区分写。
定义
点双 (\(BCC)\): 在一张无向图中,节点 \(u\) 和 \(v\) 满足 : 无论删除图上哪一个点(仅且删一个并不能是 \(u,v\) 本身) 都能够是 \(u,v\) 连通,则我们称 \(u,v\) 点双连通。
边双 (\(DCC\)): 在一张无向图中,节点 \(u\) 和 \(v\) 满足 : 无论删除图上哪一条边(仅且删一条) , \(u,v\) 都是连通的,则我们称 \(u , v\) 边双连通。
边双具有传递性,而点双不具有传递性。
即为 \(x , y\) 边双连通,\(y,z\) 边双连通,则 \(x ,z\) 边双连通。
而点双不满足。
求解边双和点双
因为边双好理解,所以先把边双放在前面。
边双 : 化整为零
边双的某些性质:
\(1.\)任意两点间至少存在两条点不重复的路径等价于图中删去任意一个点都不会改变图的连通性,即\(BCC\)中无割点
\(2.\)两个点双的公共点,就是这两个点双形成一个子图的割点(或者说是原图的割点)
\(3.\)图中一个割点一定属于至少两个点双,而一个非割点一定只属于一个点双,也就是说,割点,可以是两个以上的点双形成的公共点,但同时,一个非割点,显然,只属于一个点双。
我们很显然的知道,删除任意一条边,不改变图的连通性,那也就是只有一种情况,就是该图中没有桥。如果有桥,那么显然删除掉这一条边,图的连通性就会改变。
所以我们就有算法为 : 删桥,将图化成一个个的子图 (题目起的好形象)。
具体如下
我们先通过 \(Tarjan\) 标记出所有的桥,然后我们一遍 \(DFS\) , 这一遍 \(DFS\) 有个限制,就是不走桥,然后我们通过一系列的 \(DFS\) ,就能够求解出一个个小连通块,这里面的所有点都满足边双连通。
以下代码为求解无向图 \(G\) 中的边双连通分量的数量
有位大佬造了数据 T103489 【模板】边双连通分量
Code
//
/*
Author : Zmonarch
Knowledge :
*/
#include <bits/stdc++.h>
#define inf 2147483647
#define qwq register
#define qaq inline
#define int long long
using namespace std ;
const int kmaxn = 1e6 + 10 ;
qaq int read() {
int x = 0 , f = 1 ; char ch = getchar() ;
while(!isdigit(ch)) {if(ch == '-') f = - 1 ; ch = getchar() ;}
while( isdigit(ch)) {x = x * 10 + ch - '0' ; ch = getchar() ;}
return x * f ;
}
struct node {
int nxt , u , v ;
}e[kmaxn << 1];
int n , m , cnt , sum , tot = 1 , ans;
int h[kmaxn << 1] , low[kmaxn] , dfn[kmaxn] , id[kmaxn];
bool f[kmaxn << 1] ;
qaq void add(int u , int v) {
e[++tot].nxt = h[u] ;
e[tot].u = u ; e[tot].v = v ;
h[u] = tot ;
}
qaq void Tarjan(int u , int fa) {
low[u] = dfn[u] = ++ sum ;
for(qwq int i = h[u] ; i ; i = e[i].nxt)
{
int v = e[i].v ;
if(!dfn[v])
{
Tarjan(v , u) ;
low[u] = min(low[u] , low[v]) ;
if(dfn[u] < low[v]) f[i] = f[i ^ 1] = true ;
}
else if(v != fa) low[u] = min(low[u] , dfn[v]) ;
}
}
qaq void Dfs(int u , int in) {
id[u] = in ;
for(qwq int i = h[u] ; i ; i = e[i].nxt)
{
int v = e[i].v ;
if(id[v] || f[i]) continue ;
Dfs(v , in) ;
}
}
signed main() {
n = read() , m = read() ;
for(qwq int i = 1 ; i <= m ; i++)
{
int u = read() , v = read() ;
add(u , v) ; add(v , u) ;
}
for(qwq int i = 1 ; i <= n ; i++)
if(!dfn[i]) Tarjan(i , i) ;
for(qwq int i = 1 ; i <= n ; i++)
if(!id[i]) Dfs(i , ++ans);
printf("%lld\n" , ans) ;
return 0 ;
}
点双
点双的一个性质: 在点双连通分量中,任意两个点至少包含在一个简单环内
值得一提的两个特例
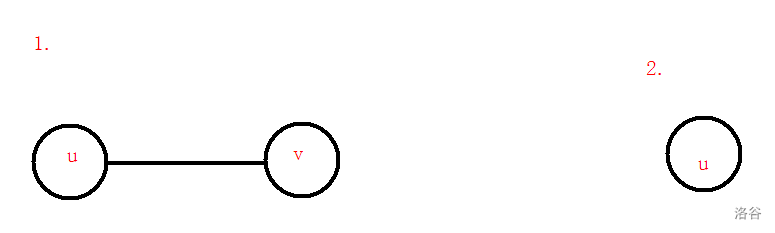
虽然不满足性质,但是满足定义。所以说是两个特例。
同样的,我们发现图中没有割点的时候,这一个图就是点双连通分量,但是根据性质,可以一个割点 \(u\) 在多个点双连通分量里面,这使得我们很棘手,如果选择求解出割点,然后删掉,不清楚 \(u\) 隶属于哪一个点双连通分量里,所以用 \(Tarjan\) 算法去维护一个栈,然后让他去找到割点,然后去弹出这一个点双连通分量,但是这时 \(u\) 不弹出 , \(u\) 还要继续去搞其他的点双连通分量
求解 : Tarjan 算法求解
简述算法 : 维护一个栈,\(DFS\)
- 若一个点是第一次被访问到,令其入栈
- 处理割点,如果遇到 \(dfn_u \leq low_v\), 我们就不断的弹出,一直弹到 \(v\) 。
还是大佬造了数据 T103492 【模板】点双连通分量
Code
//
/*
Author : Zmonarch
Knowledge :
*/
#include <bits/stdc++.h>
#define inf 2147483647
#define qwq register
#define qaq inline
#define int long long
using namespace std ;
const int kmaxn = 1e6 + 10 ;
qaq int read() {
int x = 0 , f = 1 ; char ch = getchar() ;
while(!isdigit(ch)) {if(ch == '-') f = - 1 ; ch = getchar() ;}
while( isdigit(ch)) {x = x * 10 + ch - '0' ; ch = getchar() ;}
return x * f ;
}
struct node {
int nxt , u , v ;
}e[kmaxn << 1];
int n , m , cnt , sum , tot , top;
int h[kmaxn << 1] , low[kmaxn] , dfn[kmaxn] , sta[kmaxn];
bool f[kmaxn] ;
vector<int> dcc[kmaxn] ;
qaq void add(int u , int v) {
e[++tot].nxt = h[u] ;
e[tot].u = u ; e[tot].v = v ;
h[u] = tot ;
}
qaq void Tarjan(int u , int fa) {
dfn[u] = low[u] = ++ sum ; sta[++top] = u ;
if(u == fa && !h[u]) {dcc[++cnt].push_back(u) ; return ;} // 特例 2
for(qwq int i = h[u] ; i ; i = e[i].nxt)
{
int v = e[i].v ;
if(!dfn[v])
{
Tarjan(v , u) ;
low[u] = min(low[u] , low[v]) ;
if(dfn[u] <= low[v])
{
cnt++ ; int k ;
do
{
k = sta[top--] ;
dcc[cnt].push_back(k) ;
}while(k != v) ;
dcc[cnt].push_back(u) ;
}
}
else low[u] = min(low[u] , dfn[v]) ;
}
}
signed main() {
n = read() , m = read() ;
for(qwq int i = 1 ; i <= m ; i++)
{
int u = read() , v = read() ;
add(u , v) ; add(v , u) ;
}
for(qwq int i = 1 ; i <= n ; i++)
if(!dfn[i]) Tarjan(i , i) ;
for(qwq int i = 1 ; i <= cnt ; i++)
{
for(qwq int j = 0 ; j < dcc[i].size() ; j++)
printf("%lld " , dcc[i][j]) ;
printf("\n") ;
}
return 0 ;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号