CF 757 E Bash Plays with Functions —— 积性函数与质因数分解

题目：http://codeforces.com/contest/757/problem/E

首先，f₀(n)=2^m，其中 m 是 n 的质因数的种类数；

而且

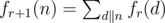
因为这个函数和1卷积，所以是一个积性函数，就可以每个质因子单独考虑；

而 f₀(p^q) = 2，对于每个质因子都一样！

所以可以 DP 预处理

而f_r(n) = f_r(p₁^e₁) * f_r(p₂^e₂) * ... * f_r(p_q^e_q)f_r(n) = dp[r][e₁] * dp[r][e₂] * ... * dp[r][e_q]

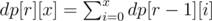
学到了质因数分解的新姿势！先预处理所有数的最小质因子，然后分解时直接除最小质因子，则复杂度就是 logn！

总之，真是一道好题！

代码如下：

#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;
typedef long long ll;
int const xn=1e6+5,mod=1e9+7;
int q,r,n,dp[xn][20],mnp[xn];
int rd()
{
  int ret=0,f=1; char ch=getchar();
  while(ch<'0'||ch>'9'){if(ch=='-')f=0; ch=getchar();}
  while(ch>='0'&&ch<='9')ret=(ret<<3)+(ret<<1)+ch-'0',ch=getchar();
  return f?ret:-ret;
}
int upt(ll x){while(x>=mod)x-=mod; while(x<0)x+=mod; return x;}
void init()
{
  int mx=1e6; mnp[1]=1;
  for(int i=2;i<=mx;i++)
    if(!mnp[i])for(int j=i;j<=mx;j+=i)mnp[j]=i;//
  dp[0][0]=1;
  for(int i=1;i<=20;i++)dp[0][i]=2;
  for(int i=1,s=0;i<=mx;i++,s=0)
    for(int j=0;j<=20;j++)s=upt(s+dp[i-1][j]),dp[i][j]=s;
}
int div(int x)
{
  int ans=1;
  while(x!=1)
    {
      int i=mnp[x],cnt=0;
      while(x%i==0)cnt++,x/=i;
      ans=((ll)ans*dp[r][cnt])%mod;
    }
  return ans;
}
int main()
{
  q=rd(); init();
  while(q--)
    {
      r=rd(); n=rd();
      printf("%d\n",div(n));
    }
  return 0;
}