流水作业调度问题——Johnson法:从两个作业到多个作业排序的正确性证明
流水作业调度问题的贪心做法———Johnson法广为人知。但关于Johnson法为什么是对的,网上常见的证明只讨论了两个作业的先后次序,然后直接根据这个次序建立了排序方法。这些证明的逻辑在于:通过对两个作业的先后次序的讨论,可以得到一种两两比较的方法;直接把这个方法应用于整个作业序列,就可以得到整个作业序列的最优执行顺序。然而,这些证明没有提到:为什么两个作业的次序可以推广到多个作业排序?下面我详细证明了这一点。
1. 问题描述
有\(n\)个作业(编号为\(1~n\))要在由两台机器\(M1\)和\(M2\)组成的流水线上完成加工。每个作业加工的顺序都是先在\(M1\)上加工,然后在\(M2\)上加工。\(M1\)和\(M2\)加工作业\(i\)所需的时间分别为\(a_i\)和\(b_i(1≤i≤n)\).
流水作业调度问题要求确定这\(n\)个作业的最优加工顺序,使得从第一个作业在机器\(M1\)上开始加工,到最后一个作业在机器\(M2\)上加工完成所需的时间最少。可以假定任何作业一旦开始加工,就不允许被中断,直到该作业被完成,即非优先调度。
2. 两个作业的次序
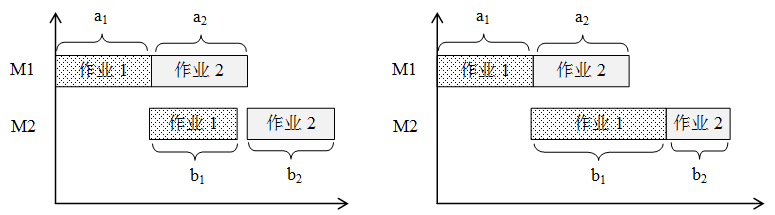
(图片来自《算法设计与分析》—李春葆)
假设先执行作业\(1\),再执行作业\(2\),此时有两种情况:\(b_1<a_2\)(左图)和 \(b_1 \geq a_2\)(右图)。在左图中,\(T=a_1+a_2+b_2\);在右图中,\(T=a_1+b_1+b_2\)。综合两种情况,我们得到:
类似地,先执行作业\(2\),再执行作业\(1\)的情况可以被表示为:
因此,我们得到结论:若 \(min(a_1,b_2)<min(a_2,b_1)\),则先执行作业\(1\),再执行作业\(2\),否则反之。进一步,有下面三种情况:
(1) \(a_1<b_1\) 且 \(a_2<b_2\) 且 \(a_1<a_2\). 此时因为 \(a_1<a_2<b_2\),故 \(min(a_1,b_2)=a_1\).又因为 \(a_1<a_2, a_1<b_1\),故 \(a_1<min(a_2,b_1)\),即 \(min(a_1,b_2)<min(a_2,b_1)\). 根据上面的结论,此时先执行作业\(1\),再执行作业\(2\)。
(2) \(a_1<b_1\) 且 \(a_2 \geq b_2\). 此时显然有\(min(a_1,b_2) \leq min(a_2,b_1)\). 由于当 \(min(a_1,b_2)=min(a_2,b_1)\) 时先执行作业\(1\)和先执行作业\(2\)用时一样,我们可以统一认为这种情况先执行作业\(1\),再执行作业\(2\)。
(3) \(a_1 \geq b_1\) 且 \(a_2 \geq b_2\) 且 \(b_1 \geq b_2\). 此时因为 \(a_1 \geq b_1 \geq b_2\),故 \(min(a_1,b_2)=b_2\).又因为 \(a_2 \geq b_2, b_1 \geq b_2\),故 \(min(a_2,b_1) \geq b_2\),即 \(min(a_1,b_2) \leq min(a_2,b_1)\). 根据上面的讨论,此时先执行作业\(1\),再执行作业\(2\)。
直接推广这三条结论,就得到了Johnson法:
(1)把所有作业按\(M1, M2\)的时间分为两组,\(a[i]≤b[i]\)对应组\(N1\),\(a[i]>b[i]\)对应组\(N2\)。
(2)将\(N1\)的作业按\(a[i]\)递增排序,\(N2\)的作业按\(b[i]\)递减排序。
(3)按顺序先执行\(N1\)的作业,再执行\(N2\)的作业,得到的就是耗时最少的最优调度方案。
3. 两个到多个的正确性
将两个元素之间的次序关系推广到多个元素,需要这种关系满足一些“序”的性质。在这里,我们采用一种简单的方法来证明:
假设当前的作业序列不是按照Johnson法提出的序排列的,我们想要证明它比Johnson法排序后的方案更差。为此,我们找到这个作业序列中第一个不满足这个序的二元对 \((P_i,P_{i+1})\),希望把 \(P_i\) 和 \(P_{i+1}\) 交换后答案变得更优。
这时,问题出现了:
(1)在 \((P_i,P_{i+1})\) 之前存在其他的作业,这些作业导致当我们处理 \((P_i,P_{i+1})\) 时,机器 \(M_1\) 可用的时间和机器 \(M_2\) 可用的时间并不是同时开始的。如下图,机器 \(M_2\) 会存在一段时间 \(st\) 被前面的作业占用。此时,情况就和我们在 2. 中的不同了。
(2)在 2. 中,我们致力于使完成两个作业的时间最短。然而在多个作业的序列中,某两个相邻作业的完成时间最短对于全局是最优的吗?也就是说,这个问题是否具有最优子结构?
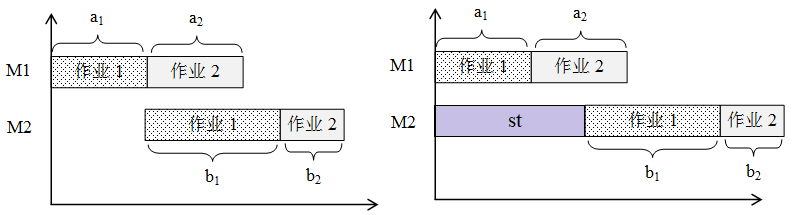
(左图为 2. 中讨论的情况,右图为多个元素的序列中两个相邻元素存在的情况)
我们逐个解决这些问题。
3.1 分类讨论
考虑到 \(st\) 的存在,我们依然可以通过分类讨论来分析各种情况下的最优策略。
3.1.1: \(a_1 \geq st\) 且 \(a_2 \geq st\)
此时 \(st\) 不影响决策,分析的过程和 2. 相同, 2. 的策略是最优的。
3.1.2: \(a_1 < st\) 且 \(a_2 < st\) 且 \(a_1+a_2 < st\)
此时不管作业\(1\)在前还是作业\(2\)在前,时间都是 \(st+b_1+b_2\). 2. 的策略也是最优的。
3.1.3: \(a_1 < st\) 且 \(a_2 < st\) 且 \(a_1+a_2 \geq st\)
此时,若先执行作业\(1\)再执行作业\(2\),则对 \(b_1\) 和 \(a_1+a_2-st\) 的大小关系进行分类讨论,可以得到最优时间 \(T=a_1+a_2+b_1+b_2+st-min(a_1+a_2,b_1+st)\). 同理,先执行作业\(2\)再执行作业\(1\)的最优时间为\(T=a_1+a_2+b_1+b_2+st-min(a_1+a_2,b_2+st)\).
(1) \(a_1<b_1\) 且 \(a_2<b_2\)
不妨设 \(a_1<a_2\). 此时,2. 的策略认为应该先执行作业\(1\)再执行作业\(2\)。我们假设此时先执行作业\(2\)再执行作业\(1\)更优,即:
(2) \(a_1<b_1\) 且 \(a_2 \geq b_2\)
此时,2. 的策略认为应该先执行作业\(1\)再执行作业\(2\)。我们仍假设先执行作业\(2\)再执行作业\(1\)更优,即有假设\(1\).
此时总有 \(a_1+a_2 < st+b_1\), 我们对 \(a_1+a_2\) 和 \(b_2+st\) 的大小关系分类讨论:
(i)设 \(a_1+a_2 < st+b_2\),那么此时 \(min(a_1+a_2,b_2+st) = a_1+a_2 = min(a_1+a_2,b_1+st)\),与假设\(1\)产生矛盾;
(ii)设 \(a_1+a_2 \geq st+b_2\),那么此时由假设\(1\)得 \(b_2+st > a_1+a_2\),产生矛盾。
(3) \(a_1 \geq b_1\) 且 \(a_2 \geq b_2\)
不妨设 \(b_1>b_2\). 此时,2. 的策略认为应该先执行作业\(1\)再执行作业\(2\)。我们仍假设先执行作业\(2\)再执行作业\(1\)更优,即有假设\(1\).
(i)设 \(a_1+a_2 < st+b_2, a_1+a_2 < st+b_1\),那么此时 \(min(a_1+a_2,b_2+st) = a_1+a_2 = min(a_1+a_2,b_1+st)\),与假设\(1\)产生矛盾;
(ii)设 \(a_1+a_2 < st+b_2, a_1+a_2 \geq st+b_1\),那么此时 \(b_1 \leq b_2\),产生矛盾;
(iii)设 \(a_1+a_2 \geq st+b_2, a_1+a_2 < st+b_1\),那么此时由假设\(1\)得 \(b_2+st > a_1+a_2\),产生矛盾;
(iv)设 \(a_1+a_2 \geq st+b_2, a_1+a_2 \geq st+b_1\),那么此时由假设\(1\)得 \(b_2 > b_1\),产生矛盾。
3.1.4: \(a_1 < st\) 且 \(a_2 \geq st\)(\(a_2 < st\) 且 \(a_1 \geq st\) 同理)
此时,若先执行作业\(1\)再执行作业\(2\),则对 \(b_1\) 和 \(a_1+a_2-st\) 的大小关系进行分类讨论,可以得到最优时间 \(T=a_1+a_2+b_1+b_2+st-min(a_1+a_2,b_1+st)\). 同理,先执行作业\(2\)再执行作业\(1\)的最优时间为\(T=a_1+a_2+b_1+b_2-min(a_1,b_2)\).
(1) \(a_1<b_1\) 且 \(a_2<b_2\)
不妨设 \(a_1<a_2\). 此时,2. 的策略认为应该先执行作业\(1\)再执行作业\(2\)。我们假设此时先执行作业\(2\)再执行作业\(1\)更优,即:
(i)设 \(a_1<b_2, a_1+a_2<st+b_1\),那么此时由假设\(2\)得 \(st-a_2>0\),产生矛盾;
(ii)设 \(a_1<b_2, a_1+a_2 \geq st+b_1\),那么此时由假设\(2\)得 \(a_1-b_1>0\),产生矛盾;
(iii)设 \(a_1 \geq b_2\),那么有 \(a_1 \geq b_2 > a_2\),产生矛盾。
(2) \(a_1<b_1\) 且 \(a_2 \geq b_2\)
此时,2. 的策略认为应该先执行作业\(1\)再执行作业\(2\)。我们仍假设此时先执行作业\(2\)再执行作业\(1\)更优,即有假设\(2\).
(i)设 \(a_1<b_2, a_1+a_2<st+b_1\),那么此时由假设\(2\)得 \(st-a_2>0\),产生矛盾;
(ii)设 \(a_1<b_2, a_1+a_2 \geq st+b_1\),那么此时由假设\(2\)得 \(-b_1+a_1>0\),产生矛盾;
(iii)设 \(a_1 \geq b_2, a_1+a_2<st+b_1\),那么此时由假设\(2\)得 \(st-a_1-a_2+b_2>0\),然而 \(st \leq a_2, b_2 \leq a_1\),产生矛盾;
(iv)设 \(a_1 \geq b_2, a_1+a_2 \geq st+b_1\),那么此时由假设\(2\)得 \(-b_1+b_2>0\),然而 \(b_1 > a_1 \geq b_2\),产生矛盾;
(3) \(a_1 \geq b_1\) 且 \(a_2 \geq b_2\)
不妨设 \(b_1>b_2\). 此时,2. 的策略认为应该先执行作业\(1\)再执行作业\(2\)。我们仍假设先执行作业\(2\)再执行作业\(1\)更优,即有假设\(2\).
注意到此时有 \(a_1 \geq b_1 \geq b_2\),故我们只需对 \(a_1+a_2\) 与 \(st+b_1\) 的大小关系进行讨论:
(i)设 \(a_1+a_2<st+b_1\),那么此时由假设\(2\)得 \(st-a_1-a_2+b_2>0\),然而 $st \leq a_2, a_1 \geq b_2 $,产生矛盾;
(ii)设 \(a_1+a_2 \geq st+b_1\),那么此时由假设\(2\)得 \(-b_1+b_2>0\),产生矛盾;
综上,在考虑 \(st\) 的情况下,2. 的策略仍然是最优策略。
3.2 最优子结构
这里,我们讨论的是:在多个作业的序列中,某两个相邻作业的完成时间最短对于全局是最优的吗?
答案是肯定的。当我们在努力使作业的完成时间最短时,我们实际上是在尽量使机器\(M2\)的结束工作时间提前(显然,\(M1\)结束工作的时间一定早与\(M2\));反映到某两个相邻的作业上,就是3.1节提出的 \(st\) 的减小,而这又只可能使它们后面两个作业的 \(st\) 减小或不变。 容易看出,某两个相邻作业的 \(st\) 减小对于整体答案只可能有好的影响。因此,某两个相邻作业的完成时间最短对于全局是最优的。
4. 总结
解决了从两个作业到多个作业的推广问题,我们再来考虑Johnson法排序的证明:假设当前的作业序列不是按照Johnson法提出的序排列的,我们想要证明它比Johnson法排序后的方案更差。为此,我们找到这个作业序列中第一个不满足这个序的二元对 \((P_i,P_{i+1})\),希望把 \(P_i\) 和 \(P_{i+1}\) 交换后答案变得更优。根据上面的讨论,这是显然的。
现在,我们可以放心地使用Johnson法了。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号