[BZOJ1116]CLO[并查集]

看了样例突然发现= =无向边不会增加入度。

然后发现是环套环。

一个环所有点入度都为2。

最后的图无视所有无向边的话大概是这样的(将就一下

 

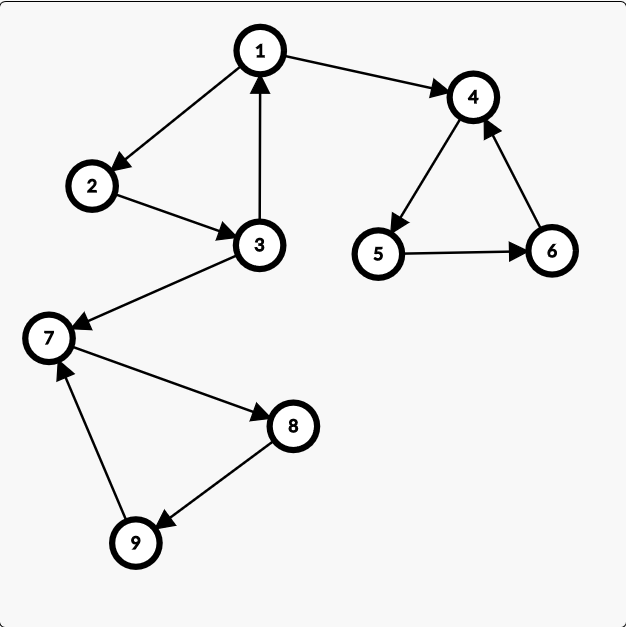
然后就可以并查集维护一下联通性...

当x , y属于一个联通块（假设是一条链），那么这条链中的每一个点都能作为根节点$root$。因为n个节点的链n-1条边只有root是入度为0的。

否则，对合并后的块(假设y所在的块并入x所在的块)，对x的块打标机。

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
inline ll _() {
    ll x=0,f=1; char ch=getchar();
    for(;ch<'0'||ch>'9';ch=getchar())
        if(ch=='-')f=-f;
    for(;ch>='0'&&ch<='9';ch=getchar())
        x=x*10+ch-'0';
    return x*f;
}
#define _ _()
const int N=1e5+5;
int f[N],vis[N];
inline int find( int x ) { return f[x]==x?x:f[x]=find(f[x]); }
int main() {
    int n=_,m=_;
    for(int i=1;i<=n;i++) f[i]=i,vis[i]=0;
    for(int i=1,x,y;i<=m;i++) {
        x=find(_); y=find(_);
        if(x==y) vis[x]=1;
        else { f[y]=x; vis[x]=vis[x]|vis[y]; }
    } 
    for(int i=1;i<=n;i++) if(!vis[find(i)]) return puts("NIE"),0;
    puts("TAK");
}