[总结]常用模板(持续更新中)
平衡树
Fhq Treap(学习链接1&&学习链接2)
以Bzoj 3224 Tyvj 1728为例
主要有两种操作(将两颗treap合并为一棵treap,或者将一棵treap拆分成两棵treap
根据这两个操作可以衍生出其他的一堆操作...
譬如插入一个数/删除一个数/查询前驱后继…(详情请点击学习链接1&&2)
效率是优秀的$O(NlogN)$

1 #include<bits/stdc++.h>
2 using namespace std;
3 typedef long long ll;
4 inline ll _() {
5 ll x=0,f=1; char ch=getchar();
6 for(;ch<'0'||ch>'9';ch=getchar())
7 if(ch=='-')f=-f;
8 for(;ch>='0'&&ch<='9';ch=getchar())
9 x=x*10+ch-'0';
10 return x*f;
11 }
12 #define _ _()
13 const int N=100005;
14 int son[N][2],val[N],rnd[N],siz[N],cnt,root;
15 inline void up(int x) {
16 siz[x]=siz[son[x][0]]+siz[son[x][1]]+1;
17 }
18 inline int newnode(int x) {
19 siz[++cnt]=1;
20 val[cnt]=x;
21 rnd[cnt]=rand();
22 return cnt;
23 }
24 inline int merge(int x,int y) {
25 if(!x||!y) return x+y;
26 if(rnd[x]<rnd[y]) {
27 son[x][1]=merge(son[x][1],y);
28 up(x);
29 return x;
30 }else {
31 son[y][0]=merge(x,son[y][0]);
32 up(y);
33 return y;
34 }
35 }
36 inline void spilt(int rt,int a,int &x,int &y) {
37 if(!rt) x=y=0;
38 else {
39 if(val[rt]<=a) {
40 x=rt;
41 spilt(son[rt][1],a,son[rt][1],y);
42 }else {
43 y=rt;
44 spilt(son[rt][0],a,x,son[rt][0]);
45 }
46 up(rt);
47 }
48 }
49 inline int kth(int rt,int k) {
50 while(1) {
51 if(k<=siz[son[rt][0]])
52 rt=son[rt][0];
53 else
54 if(k==siz[son[rt][0]]+1)
55 return rt;
56 else
57 k-=siz[son[rt][0]]+1,rt=son[rt][1];
58 }
59 }
60 int main() {
61 srand((unsigned)time(NULL));
62 int n=_,x,y,z;
63 for(int i=1;i<=n;i++) {
64 int opt=_,a=_;
65 if(opt==1) {
66 spilt(root,a,x,y); //直接分成两颗树
67 root=merge(merge(x,newnode(a)),y); //把三棵树合并起来
68 }else
69 if(opt==2) {
70 spilt(root,a,x,z); //按a为边界分为x和z两颗树,x中的数<=a,z中的数>a
71 spilt(x,a-1,x,y); //按a-1为边界分为两颗树,现在共有三棵树,x<a,y=a,z>a
72 y=merge(son[y][0],son[y][1]); //把y的左右孩子合并起来,则删掉了y的根节点
73 root=merge(merge(x,y),z);
74 }else
75 if(opt==3) {
76 spilt(root,a-1,x,y);
77 printf("%d\n",siz[x]+1);
78 root=merge(x,y);
79 }else
80 if(opt==4) {
81 printf("%d\n",val[kth(root,a)]);
82 }else
83 if(opt==5) {
84 spilt(root,a-1,x,y); //按a-1为边界划分为两颗树,y中的数>=a,x中的数<a
85 printf("%d\n",val[kth(x,siz[x])]); //前驱为x中的最大值
86 root=merge(x,y);
87 }else
88 if(opt==6) {
89 spilt(root,a,x,y); //按a为边界划分为x和y两颗树,y中的数>a,x中的数<=a
90 printf("%d\n",val[kth(y,1)]); //前驱为y中的最小值
91 root=merge(x,y);
92 }
93 }
94 }
上面那是普通平衡树都能解决的操作。也就是对单独元素的操作。
但是遇到的一般是区间操作。比如区间翻转什么的。
以Bzoj 3223 Tyvj 1729为例。
区间操作的话一般是按siz来split; 设两个哨兵一样的东西(1和n+2)
然后把1~n分成1~l-1,l~r,r+1~n;
那么我只需要按l为边界split一次,按r+1为边界再split一次就行了。(如果没有边界1,n+2的话,需要按l-1split一次,rsplit一次)
修改中间那段(l~r)。
区间翻转的话打个标记就行了。
效率仍然是优秀的$O(NlogN)$
参考的是attack大佬的模板

1 #include<bits/stdc++.h>
2 using namespace std;
3 typedef long long ll;
4 inline ll _() {
5 ll x=0,f=1; char ch=getchar();
6 for(;ch<'0'||ch>'9';ch=getchar())
7 if(ch=='-')f=-f;
8 for(;ch>='0'&&ch<='9';ch=getchar())
9 x=x*10+ch-'0';
10 return x*f;
11 }
12 #define _ _()
13 const int N=100005;
14 int son[N][2],val[N],rnd[N],siz[N],tot,root,tag[N];
15 int n,m;
16 inline void up(int rt) {
17 siz[rt]=siz[son[rt][0]]+siz[son[rt][1]]+1;
18 }
19 inline int newnode(int x) {
20 val[++tot]=x;
21 siz[tot]=1;
22 rnd[tot]=rand();
23 return tot;
24 }
25 inline void down(int x) {
26 if(x&&tag[x]) {
27 tag[x]=0;
28 swap(son[x][0],son[x][1]);
29 if(son[x][0]) tag[son[x][0]]^=1;
30 if(son[x][1]) tag[son[x][1]]^=1;
31 }
32 }
33 inline int build(int l,int r) {
34 if(l>r) return 0;
35 int mid=(l+r)>>1; int v=mid-1;
36 int now=newnode(v);
37 son[now][0]=build(l,mid-1);
38 son[now][1]=build(mid+1,r);
39 up(now);
40 return now;
41 }
42 inline int merge(int x,int y) {
43 if(!x||!y) return x+y;
44 down(x); down(y);
45 if(rnd[x]<rnd[y]) {
46 son[x][1]=merge(son[x][1],y);
47 up(x);
48 return x;
49 }else {
50 son[y][0]=merge(x,son[y][0]);
51 up(y);
52 return y;
53 }
54 }
55 inline void split(int rt,int k,int &x,int &y) { //区间操作时要按siz分
56 if(!rt) x=y=0;
57 else {
58 down(rt);
59 if(k<=siz[son[rt][0]]){
60 y=rt;
61 split(son[rt][0],k,x,son[rt][0]);
62 } else {
63 x=rt;
64 split(son[rt][1],k-siz[son[rt][0]]-1,son[rt][1],y);
65 }
66 up(rt);
67 }
68 }
69 inline void reverse(int l,int r) {
70 int x,y,a,b;
71 split(root,r+1,x,y);
72 split(x,l,a,b);
73 tag[b]^=1;
74 root=merge(merge(a,b),y);
75 }
76 inline void dfs(int x) {
77 if(!x) return;
78 down(x);
79 dfs(son[x][0]);
80 if(val[x]>=1&&val[x]<=n) printf("%d ",val[x]);
81 dfs(son[x][1]);
82 }
83 int main() {
84 srand((unsigned)time(NULL));
85 n=_; m=_;
86 root=build(1,n+2);
87 while(m--) {
88 int l=_,r=_;
89 reverse(l,r);
90 }
91 dfs(root);
92 }
树链剖分
通过把一棵树划分成若干条重链。然后通过不断地爬重链来更新答案。
(u,v)的路径最多经过logn条重链。
比如这棵树

重儿子就是深色的那些节点

然后图中有这么些重链:(2,2) , (1,3) , (4,4)。共三条。
复杂度是$O(NlogN)$
然后上面往往会加点什么数据结构维护一下。
比如树状数组/线段树。那么效率是$O(Nlog^2N)$
模板:BZOJ1036

1 #include<cstdio>
2 #include<cmath>
3 #include<iostream>
4 #define inf 0x7fffffff
5 struct pos{int to,nxt;}e[60005];
6 int cnt,head[30005];
7 int n,sum[150005],mx[150005],a[30005],flag[150005];
8 int rev[30005],siz[30005],seg[30005],top[30005],dep[30005],f[30005],son[30005];
9 inline void add(int u,int v) {
10 e[++cnt]=(pos){v,head[u]};
11 head[u]=cnt;
12 }
13 inline int max(int a,int b) {
14 return a>b?a:b;
15 }
16 inline void up(int rt) {
17 sum[rt]=sum[(rt << 1)]+sum[(rt << 1)|1];
18 mx[rt]=max(mx[(rt << 1)],mx[(rt << 1)|1]);
19 }
20 inline void build(int l,int r,int rt){
21 if(l==r) {sum[rt]=mx[rt]=a[rev[l]];return;}
22 int mid=(l+r) >> 1;
23 build(l,mid,rt << 1);
24 build(mid+1,r,(rt << 1)|1);
25 up(rt);
26 }
27 inline void down(int rt,int ln,int rn) {
28 if(flag[rt]) {
29 mx[(rt << 1)]=flag[rt];
30 mx[(rt << 1)|1]=flag[rt];
31 sum[(rt << 1)]=flag[rt]*ln;
32 sum[(rt << 1)|1]=flag[rt]*rn;
33 flag[rt << 1]=flag[rt];
34 flag[(rt << 1)|1]=flag[rt];
35 flag[rt]=0;
36 }
37 }
38 inline void add(int l,int r,int v,int L,int R,int rt) {
39 if(l<=L&&R<=r) {
40 sum[rt]=(R-L+1)*v;
41 flag[rt]=v;
42 mx[rt]=v;
43 return;
44 }
45 int mid=(L+R) >> 1;
46 down(mid,mid-L+1,R-mid);
47 if(l<=mid) add(l,r,v,L,mid,rt << 1);
48 if(r>mid) add(l,r,v,mid+1,R,(rt << 1)|1);
49 up(rt);
50 }
51 inline int query1(int l,int r,int L,int R,int rt) {
52 if(l<=L&&R<=r) return mx[rt];
53 int mid=(L+R) >> 1,ans=-inf;
54 down(mid,mid-L+1,R-mid);
55 if(l<=mid) ans=max(ans,query1(l,r,L,mid,(rt << 1)));
56 if(r>mid) ans=max(ans,query1(l,r,mid+1,R,(rt <<1)|1));
57 return ans;
58 }
59 inline int query2(int l,int r,int L,int R,int rt) {
60 if(l<=L&&R<=r) return sum[rt];
61 int mid=(L+R) >> 1,ans=0;
62 down(mid,mid-L+1,R-mid);
63 if(l<=mid) ans+=query2(l,r,L,mid,(rt << 1));
64 if(r>mid) ans+=query2(l,r,mid+1,R,(rt << 1)|1);
65 return ans;
66 }
67 inline void dfs1(int u) {
68 dep[u]=dep[f[u]]+1; siz[u]=1;
69 for(int i=head[u];i;i=e[i].nxt) {
70 if(e[i].to!=f[u]) {
71 f[e[i].to]=u;
72 dfs1(e[i].to);
73 siz[u]+=siz[e[i].to];
74 if(siz[son[u]]<siz[e[i].to])
75 son[u]=e[i].to;
76 }
77 }
78 }
79 inline void dfs2(int u) {
80 if(son[u]) {
81 seg[son[u]]=++seg[0];
82 top[son[u]]=top[u];
83 rev[seg[0]]=son[u];
84 //rev[seg[son[u]]]=son[u];
85 dfs2(son[u]);
86 }
87 for(int i=head[u];i;i=e[i].nxt) {
88 int v=e[i].to;
89 if(!top[v]){
90 seg[v]=++seg[0];
91 rev[seg[0]]=v;
92 top[v]=v;
93 dfs2(v);
94 }
95 }
96 }
97 inline int ask1(int x,int y) {
98 int ans=-inf,fx=top[x],fy=top[y];
99 while(fx!=fy) {
100 if(dep[fx]<dep[fy])std::swap(x,y),std::swap(fx,fy);
101 ans=max(ans,query1(seg[fx],seg[x],1,seg[0],1));
102 x=f[fx];fx=top[x];
103 }
104 if(dep[x]>dep[y])std::swap(x,y);
105 ans=max(ans,query1(seg[x],seg[y],1,seg[0],1));
106 return ans;
107 }
108 inline int ask2(int x,int y) {
109 int ans=0,fx=top[x],fy=top[y];
110 while(fx!=fy) {
111 if(dep[fx]<dep[fy])std::swap(fx,fy),std::swap(x,y);
112 ans+=query2(seg[fx],seg[x],1,seg[0],1);
113 x=f[fx];fx=top[x];
114 }
115 if(dep[x]>dep[y])std::swap(x,y);
116 ans+=query2(seg[x],seg[y],1,seg[0],1);
117 return ans;
118 }
119 int main() {
120 scanf("%d",&n);
121 for(int i=1;i<n;i++) {
122 int u,v;
123 scanf("%d%d",&u,&v);
124 add(u,v);add(v,u);
125 }
126 seg[0]=seg[1]=top[1]=rev[1]=1;
127 dfs1(1);
128 dfs2(1);
129 for(int i=1;i<=n;i++)
130 scanf("%d",&a[i]);
131 build(1,seg[0],1);
132 int q;
133 scanf("%d",&q);
134 while(q--) {
135 char op[10];
136 int u,v;
137 scanf("%s%d%d",op,&u,&v);
138 if(op[0]=='C')
139 add(seg[u],seg[u],v,1,seg[0],1);
140 else
141 if(op[1]=='M')
142 printf("%d\n",ask1(u,v));
143 else
144 printf("%d\n",ask2(u,v));
145 }
146 }
线段树
把一段区间分成若干个子区间然后通过合并子区间的信息来获取整个区间信息的数据结构...

比如这样。然后我可以维护子区间的和/最大值/最小值…
然后修改的话直接对完整的区间打标记就好了。什么叫做完整的区间。比如上面这个图。我找不到[2,4],所以我得拆成[2,2]和[3,4]。然后分别对着两个区间打延迟标记。比如加法[2,4]+1 即 [2,2]+1 && [3,4]+1
查询的话同理。统计完整的区间的答案。完整的区间定义如上。然后如果我要求[2,4]的和。可以拆成[2,2]的和+[3,4]的和。
细节可以看代码...
但是处理多个标记的话要注意标记间的相互作用。比如乘法和加法我要先下传乘法再下传加法。
这玩意效率是$O(N+QlogN)$,但是因为你分解区间所以是很多个$logN$

1 #include<bits/stdc++.h>
2 using namespace std;
3 typedef long long LL;
4 typedef unsigned long long ULL;
5 typedef unsigned int uint;
6 #define lson (rt << 1)
7 #define rson ((rt << 1)|1)
8 #define mid ((l+r) >> 1)
9 const int N=1e5+5;
10 int n,m;
11 struct sgt{int l,r,flag;LL sum;}t[N << 2];
12 inline void pushup(int rt) {t[rt].sum=t[(rt << 1)].sum+t[(rt << 1)|1].sum;}
13 inline void build(int l,int r,int rt) {
14 t[rt].l=l; t[rt].r=r;
15 if(l==r){scanf("%lld",&t[rt].sum);return;}
16 build(l, mid, lson);
17 build(mid+1,r,rson);
18 pushup(rt);
19 }
20 inline void pushdown(int rt,int ln,int rn) {
21 if(t[rt].flag) {
22 t[lson].flag+=t[rt].flag;
23 t[rson].flag+=t[rt].flag;
24 t[lson].sum+=t[rt].flag*ln;
25 t[rson].sum+=t[rt].flag*rn;
26 t[rt].flag=0;
27 }
28 }
29 inline void add(int L,int R,int v,int rt) {
30 int l=t[rt].l,r=t[rt].r;
31 if(L<=l&&r<=R){t[rt].sum+=1ll*v*(r-l+1); t[rt].flag+=v;return;}
32 pushdown(rt,mid-l+1,r-mid);
33 if(L<=mid) add(L,R,v,lson);
34 if(R> mid) add(L,R,v,rson);
35 pushup(rt);
36 }
37 inline LL ask(int L,int R,int rt) {
38 int l=t[rt].l,r=t[rt].r;
39 if(L<=l&&r<=R)return t[rt].sum;
40 pushdown(rt,mid-l+1,r-mid);
41 LL ans=0;
42 if(L<=mid)ans+=ask(L,R,lson);
43 if(R> mid)ans+=ask(L,R,rson);
44 return ans;
45 }
46 inline void solve() {
47 char op[10];
48 int l,r,v;
49 scanf("%s %d%d",op,&l,&r);
50 if(op[0]=='Q')printf("%lld\n",ask(l,r,1));
51 else {
52 scanf("%d",&v);
53 add(l,r,v,1);
54 }
55 }
56 int main() {
57 scanf("%d%d",&n,&m);
58 build(1,n,1);
59 while(m--)solve();
60 }
其实有一种更加神奇的东西叫做。。。线段树合并。。。
其实我是根据Fhq-Treap的合并来感性理解线段树合并的效率的--$O(logN)$
虽然这玩意能$split$但是貌似没啥作用。
然后在合并的时候维护一下各节点的信息比如。sum,max,min…
具体的说合并就是两颗线段树x,y。他们要合并成一棵。对于两颗树的公共节点(因为是权值线段树,所以树的形态都是一样的),新建一个节点,然后存储这个公共节点合并后的值。如果是sum就sum[newtot]=sum[nowx]+sum[nowy]。如果是max||min就直接新建节点就好了。因为你没办法通过两个非叶子节点的值的合并来得到新节点的值。
其实max的话只需要把叶子节点的值直接加起来(因为l==r的时候,max是可以直接合并的)然后再update一下就好了。
然后因为不能开M棵有n个节点的权值线段树(会MLE的嘛)。于是就采用动态开点的方式。(其实就是存一下son[x][0/1]表示这个点的左儿子和右儿子)
附丑图一张。
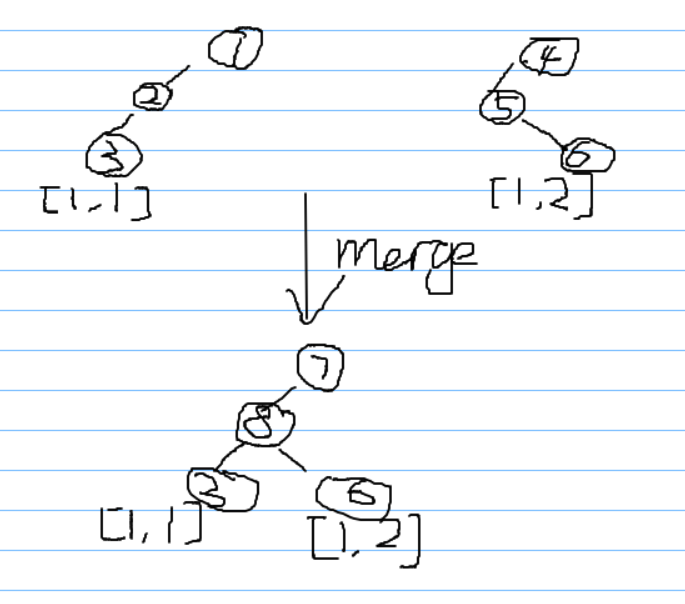
以Bzoj 5457为例
效率是$O(MlogN)$

1 #include<bits/stdc++.h>
2 using namespace std;
3 typedef long long ll;
4 inline ll _() {
5 ll x=0,f=1; char ch=getchar();
6 for(;ch<'0'||ch>'9';ch=getchar())
7 if(ch=='-')f=-f;
8 for(;ch>='0'&&ch<='9';ch=getchar())
9 x=x*10+ch-'0';
10 return x*f;
11 }
12 #define _ _()
13 const int N=8e5+5;
14 struct Edge { int to,nxt; }e[N<<1];
15 int head[N],cnt;
16 inline void insert( int u,int v ) {
17 e[cnt]=(Edge) { v,head[u] }; head[u]=cnt++;
18 }
19 inline void ins( int u,int v ) {
20 insert(u,v); insert(v,u);
21 }
22 int n,m,a[N],b[N];
23 int mx[20*N],pos[20*N],son[20*N][2],ans[N],ans2[N],rt[N],tot;
24 inline void up( int x ) {
25 mx[x]=max(mx[son[x][0]],mx[son[x][1]]);
26 if(mx[son[x][0]]>=mx[son[x][1]])
27 pos[x]=pos[son[x][0]];
28 else
29 pos[x]=pos[son[x][1]];
30 }
31 inline int newtree( int x,int v,int l,int r ) {
32 /*sum[++tot]=v;*/ mx[++tot]=v; pos[tot]=x;
33 if(l==r) return tot;
34 int mid=(l+r)>>1,now=tot;
35 if(x<=mid) son[now][0]=newtree(x,v,l,mid);
36 else son[now][1]=newtree(x,v,mid+1,r);
37 return now;
38 }
39 inline int merge( int x,int y,int l,int r ) {
40 if(!x||!y) return x+y;
41 /*sum[++tot]=sum[x]+sum[y];*/
42 ++tot;
43 if(l==r) { mx[tot]=mx[x]+mx[y]; pos[tot]=l; return tot; }
44 int mid=(l+r) >> 1,now=tot;
45 son[now][0]=merge(son[x][0],son[y][0],l,mid);
46 son[now][1]=merge(son[x][1],son[y][1],mid+1,r);
47 up(now);
48 return now;
49 }
50 inline void dfs( int x,int fa ) {
51 for(int i=head[x];~i;i=e[i].nxt) {
52 if(e[i].to!=fa) {
53 dfs(e[i].to,x);
54 rt[x]=merge(rt[x],rt[e[i].to],1,m);
55 }
56 }
57 ans[x]=pos[rt[x]];
58 ans2[x]=mx[rt[x]];
59 }
60 int main() {
61 n=_; m=_;
62 memset(head,-1,sizeof(head));
63 for(int i=1,u,v;i<n;i++) {
64 u=_; v=_;
65 ins(u,v);
66 }
67 for(int i=1;i<=n;i++)
68 a[i]=_,b[i]=_,rt[i]=newtree(a[i],b[i],1,m);
69 dfs(1,0);
70 for(int i=1;i<=n;i++)
71 printf("%d %d\n",ans[i],ans2[i]);
72 }
带权并查集
因为并查集妇孺皆知,所以直接贴模板…
合并$(x,y)$就把x这个节点所在树的根节点找出来,y同理。如果两个点的根节点相同,则证明是同一颗树,不需要再合并了。
有两种优化的方法,把轻的树合并到重的树上来保证树的平衡,或者直接把所有节点并到根节点下。

1 //路径压缩
2 inline int find( int x ) { return pre[x]==x?x:pre[x]=find(pre[x]); }
然后是带权并查集。
一般是求解这样的一类问题:给定若干组条件:$[l,r]$的区间和是val。然后若干组询问$[l,r]$的区间和为val是否符合条件
看到的话一头雾水...实际上如果做过Bzoj1984应该就懂了一些什么...
边权下放...也即$x->y$有一条w的边的话,可以看做y的权值为w(适用于树)
所以咋做我还是不会...
蓝鹅带权并查集是把x的权值看成-w...
对于$[l,r]$,他的区间和显然可以通过之前的条件推出来...
比如我可以通过已知的[1,5]和[6,10]推出[1,10]的区间和。
前缀和!$sum[r]-sum[l-1]$给了一点启发。
总结一下就...如果两个节点不在同一颗树里。那就把两颗树合并起来。合并的时候相当于$(fx,fy)$在合并。但是fx->fy并不知道。所以要算一下,发现是sum[y]-sum[x]-w;(因为实际上我们把值存边权的负数)

1 #include<bits/stdc++.h> 2 using namespace std; 3 typedef long long ll; 4 inline ll _() { 5 ll x=0,f=1; char ch=getchar(); 6 for(;ch<'0'||ch>'9';ch=getchar()) 7 if(ch=='-')f=-f; 8 for(;ch>='0'&&ch<='9';ch=getchar()) 9 x=x*10+ch-'0'; 10 return x*f; 11 } 12 #define _ _() 13 int sum[105],pre[105],n,m; 14 inline int find( int x ) { 15 if(pre[x]==x) return x; 16 else { 17 int fx=find(pre[x]); 18 sum[x]+=sum[pre[x]]; 19 return pre[x]=fx; 20 } 21 } 22 int main() { 23 int t=_; 24 while(t--) { 25 n=_; m=_; 26 bool flag=true; 27 for(int i=0;i<=n;i++) pre[i]=i,sum[i]=0; 28 while(m--) { 29 int x=_-1,y=_,val=_,fx=find(x),fy=find(y); 30 if(fx==fy) { if(sum[y]-sum[x]!=val) flag=0; } 31 else { 32 pre[fx]=fy; 33 sum[fx]=sum[y]-sum[x]-val; 34 } 35 } 36 for(int i=1;i<=n;i++) 37 printf("%d ",sum[i]); 38 puts(flag?"true":"false"); 39 } 40 }


