N1CTF 2022
ezdlp
题目:
ezdlp.py
from Crypto.Util.number import *
from math import prod
from secret import flag
def keygen(pbits,kbits,k):
p = getPrime(pbits)
x = [getPrime(kbits + 1) for i in range(k)]
y = prod(x)
while 1:
r = getPrime(pbits - kbits * k)
q = 2 * y * r + 1
if isPrime(q):
return p*q, (p, q, r, x)
def encrypt(key, message):
return pow(0x10001, message, key)
key = keygen(512, 24, 20)
flag = bytes_to_long(flag)
messages = [getPrime(flag.bit_length()) for i in range(47)] + [flag]
enc = [encrypt(key[0], message) for message in messages]
print(messages[:-1])
print(enc)
分析:
1.加密和困难性分析
题目的keygen是生成光滑素数p和q的函数,而encrypt是进行乘方模的函数,其中message作为指数;整体的加密流程很简单,反复随机生成若干个和flag的bit长度相同的数进行encrypt,但是没给n;一旦我们拿到n就可以通过p-1算法分解n拿到p,并且在模p下计算离散对数,即flag。所以难点有两个,一个是求n,另一个是p-1算法的时间复杂度较大,需要另辟蹊径。
2.利用格基规约恢复n
这一步可以参考maple大佬出的一个题,我这里还是来分析一下。
我们假设每一组已知的message为\(e_i\),输出的密文记为\(c_i\),我们去找一组系数\(a_i\),使得满足如下关系:
为了找到这样一组系数,我们构造如下的格:
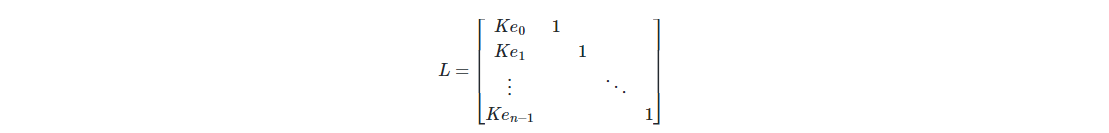
其实非常类似背包的构造,但是对第一列乘了一个较大的数字K,这是为了限制规约后的最短向量的第一维是0;关于这里我测试了不乘k,结果发现第一组最小向量的第一维是54,乘上k的话这个54会扩大很多倍,自然就不满足最短向量这一条件了,也就是排除非0的结果。当然即使不是0的最短向量系数也是能做的但是会麻烦一点,就不讨论了。
这里规约出来得到的系数就是\(a_i\)了,并且是有正有负的,接下来计算每一组\(c_i^{a_i}\)并把n组连续相乘起来,记为s,则\(s-1\equiv0\;mod\;n\),注意这里的s由于\(a_i\)有负数所以是个分数,那么记为\(\frac{x}{y}-1\;\equiv0\;mod\;n\)。通分以后得到\(x-y\;\equiv0\;mod\;n\),那么用两组x和y,计算\(gcd(x_0-y_0,x_1-y_1)\)就是n了。
3.根据keygen可知,其中的小素数最大的是r,bit为512-24.20=32,其余的都是25bit,那么改写p-1算法,即使只把所有的素数相乘,也有一个32bit的需要去遍历,这个时间复杂度是相当大的,用python写的话太慢了,需要用c实现或者利用现有的工具计算。github有一个大数分解的工具gmp-ecm,p-1算法的使用方法见项目readme:

在未知p-1的任何一个因子的情况下,我们需要找到一个上界B2,即所有因子都小于它,这里就是\(\small 2^{32}=4294967296\);次上界B1,只有一个因子大于它,这里是\(\small 2^{25}=33554432\),那么使用命令
echo 131158523227880830085100826212925738665356578827561846263073537503153187073136528966506785633847097997799377037969243883439723340886038624250936927221630287086602285835045356221763554989140952262353930420392663280482277832613695689454662506372252641564106136178637816827646124189347219273164844809807934422046441 | ecm -pm1 33554432 4294967296
能在30s以内分解成功。
拿到p和q以后在模p下求离散对数即可。
exp:
from Crypto.Util.number import *
print(2^32)
print(2^25)
with open('ezdlp.txt') as f:
msgs = eval(f.readline())
enc = eval(f.readline())
# T是转置,augment是把两个矩阵左右相连扩展,identity是单位矩阵
M = matrix(ZZ, msgs).T.augment(matrix.identity(len(msgs)))
# 每一行的第0列乘上一个较大的k,其他列不变
M[:,0] *= 2^100
M = M.LLL()
print(M[0])
print(M[1])
aa = product([ZZ(x)^y for x,y in zip(enc, M[0][1:])])
bb = product([ZZ(x)^y for x,y in zip(enc, M[1][1:])])
# numer是分子 denom是分母
n = gcd(aa.numer() - aa.denom(), bb.numer() - bb.denom())
print(n)
n = 131158523227880830085100826212925738665356578827561846263073537503153187073136528966506785633847097997799377037969243883439723340886038624250936927221630287086602285835045356221763554989140952262353930420392663280482277832613695689454662506372252641564106136178637816827646124189347219273164844809807934422046441
q = 12980311456459934558628309999285260982188754011593109633858685687007370476504059552729490523256867881534711749584157463076269599380216374688443704196597025947
p = n // q
m = GF(q)(enc[-1]).log(0x10001)
flag = long_to_bytes(int(m))
print(flag)
brand_new_checkin
题目:
brand_new_checkin.py
from Crypto.Util.number import *
from random import getrandbits
from secret import flag
def keygen():
p = getPrime(512)
q = getPrime(512)
n = p * q
phi = (p-1)*(q-1)
while True:
a = getrandbits(1024)
b = phi + 1 - a
s = getrandbits(1024)
t = -s*a * inverse(b, phi) % phi
if GCD(b, phi) == 1:
break
return (s, t, n), (a, b, n)
def enc(m, k):
s, t, n = k
r = getrandbits(1024)
return m * pow(r, s, n) % n, m * pow(r, t, n) % n
pubkey, privkey = keygen()
flag = pow(bytes_to_long(flag), 0x10001, pubkey[2])
c = []
for m in long_to_bytes(flag):
c1, c2 = enc(m, pubkey)
c.append((c1, c2))
print(pubkey)
print(c)
分析:
1.加密和困难性分析
题目有两个难点,1是利用MT19937还原a,而是通过a和其他已知信息推导phi求d解密。
2.关于MT19937
这里的enc函数m * pow(r, s, n) % n, m * pow(r, t, n) % n实际上存在共模攻击漏洞,而m是flag的rsa密文的每一个字节,这里可以通过遍历1-255来确认正确的m。然后可以恢复pow(r, s, n)和pow(r, t, n),利用共模攻击求\(r\;mod\;n\),实际上r的比特是小于1024,由于n为1023bit长,所以可能大于n,这里就需要爆破一下,可以找到距离\(2^{1024}\)最近的20个连续的\(r\;mod\;n\)进行爆破以缩小时间复杂度。爆破恢复随机数序列以后可以预测几个数来判断是否正确。然后反推a就可以了。
2.关于求phi
已知\(a+b \equiv 1\;mod\;\phi\;\;as+bt\equiv0\;mod\;\phi\)
那么联立解就能得到\(at-as\equiv \; t\;mod\; \phi\),用k.phi求d即可,脚本又长又丑,就不放了。
babyecc
题目:
babyecc.sage
from Crypto.Util.number import *
from secret import flag
m = Integer(int.from_bytes(flag, 'big'))
for _ in range(7):
p = getPrime(512)
q = getPrime(512)
n = p * q
while 1:
try:
a = randint(0,n)
b = randint(0,n)
Ep = EllipticCurve(GF(p), [a,b])
Gp = Ep.lift_x(m) * 2
Eq = EllipticCurve(GF(q), [a,b])
Gq = Eq.lift_x(m) * 2
y = crt([int(Gp[1]),int(Gq[1])],[p,q])
break
except Exception as err:
pass
print(n, a, b, y)
分析:
因为是赛后复现,做法基本上参考的NeSE战队的思路。
1.加密和困难性分析
题目给了七轮的加密,每次随机选取大素数p q,产生两条椭圆曲线Ep和Eq,然后在两条曲线上各取一点,计算它们的倍点,利用crt计算倍点的y值,这里相当于生成了一条新的mod n的椭圆曲线。这种类型的题目基本都是要用椭圆曲线的坐标计算公式来建立方程,这题特殊的地方在于用coppersmith求解的时候需要用crt组一下。
2.首先明确一下倍点公式,也就是:
由(1)得\(x_r=(\frac{3m^2 +a}{2y_p})^2 -2m\rightarrow \frac{(3m^2+a)^2}{4(m^3+am+b)}-2m \qquad (2)\)
再联立ecc方程(3)
可以设\(k = 4(m^3+am+b),c=(3m^2+a)\),带入计算得:
3.由2我们已经建立了模n下的方程式,接下来就是求解的问题。
其实这就是一个广播攻击而已,很多论文中都有,就是利用crt将模数N的比特位提高,然后使其满足coppersmith的界。

增大N,copper的界\(N^{\frac{1}{d}-\epsilon}\)也随之增大了,为此我们在求解的时候还应该尽量减小\(\epsilon\)的值,进一步扩大界。进行估算以验证copper的有效性,维数是12,crt以后的N是7 * 1024bit,\(N^{\frac{1}{12}}\)大约600bit,flag格式是uuid所以比特大概为300-400,所以可行。后面就是写exp了。
exp:
from Crypto.Util.number import *
lines = open("babyecc.txt","r").readlines()
fs = []
ns = []
def Function(n,a,b,y):
P.<m> = PolynomialRing(Zmod(n))
k = 4*(m^3+a*m+b)
c = (3*m^2+a)^2
f = k^3*y^2 - (c-2*m*k)^3 - a*(k^2*c-2*m*k^3) - b*k^3
return f
for line in lines:
n,a,b,y = [ZZ(i) for i in line.strip().split(" ")]
f = Function(n,a,b,y).monic().change_ring(ZZ)
fs.append(f)
ns.append(n)
F = crt(fs,ns)
N = prod(ns)
FF = F.change_ring(Zmod(N))
roots = FF.small_roots(epsilon = 0.03)
print(roots)
print(long_to_bytes(int(roots[0])))
# n1ctf{7140f171-5fb5-484d-92f4-9f7ba02c33d0}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号