强网杯全国网络安全挑战赛 2023
这次主要做了misc得分,crypto后面好好复现一下。
已解决
强网先锋
SpeedUp
非预期,google找到该问题的序列值:
A244060 - OEIS
直接找27对应的值做哈希即可:
from hashlib import sha256
secret = b'4495662081'
flag = sha256(secret).hexdigest()
print(flag)
sagemath的factorial函数,可高效算阶乘,然后转str处理:
a = factorial(2^27)
b = str(a)
from tqdm import tqdm
res = 0
for each in tqdm(b):
res += int(each)
print(res)
石头剪刀布
根据MultinomialNB知道是用的多项式朴素贝叶斯,搜索一下原理:
Python · 朴素贝叶斯(二)· MultinomialNB - 知乎 (zhihu.com)
一文读懂贝叶斯原理(Bayes‘ theorem)_bayes' theorem-CSDN博客
可知该模型原理为利用支持某项属性的事件发生得愈多,则该事件发生的的可能性就愈大,结合server代码:
def predict(i,my_choice):
global sequence
model = None
if i < 5:
opponent_choice = [random.randint(0, 2)]
else:
model = train_model(X_train, y_train)
opponent_choice = predict_opponent_choice(model, [sequence])
# ...Constructing a training set...#
return opponent_choice
可以知道这里是抹去了划分训练集的过程并且应该是利用对方前几次出拳作为数据集训练模型进行预测,根据代码:
if i < 5:
opponent_choice = [random.randint(0, 2)]
else:
model = train_model(X_train, y_train)
opponent_choice = predict_opponent_choice(model, [sequence])
可知使用小于5次的结果来进行训练,为了提高模型准确率,直接猜测是4,那么对于landa,只要随机出拳四次,然后用这四次去训练模型预测结果,放入tmp_list,每次取当前最新的4次出拳结果训练即可,这就得到Me10n的每次的出拳情况,然后根据Me10n的出拳调整我方landa的出拳即可。exp:
from pwn import*
from sklearn.naive_bayes import MultinomialNB
from random import randint
import numpy as np
io=remote('8.147.131.224',19127)
trains = []
trains_tag = []
tmp_list = []
for i in range(100):
print(f'第{i}轮')
io.recvuntil('请出拳(0 - 石头,1 - 剪刀,2 - 布):'.encode('utf-8'))
if i >= 5:
x=tmp_list[i-4:i]
model = MultinomialNB()
model.fit(np.array(trains), np.array(trains_tag))
y=model.predict(np.array(x).reshape(1, -1))
landa_choice=(y[0]+1)%3
trains.append(x)
trains_tag.append(landa_choice)
else:
landa_choice=randint(0, 2)
if i == 4:
x=tmp_list[:i]
y=landa_choice
trains.append(x)
trains_tag.append(y)
tmp_list.append(landa_choice)
io.sendline(str(landa_choice).encode())
for i in range(5):
print(io.recvline().decode())
print(io.recvline())
easyfuzz
直接手测一下可以发现必须是9字节才能对应,那么试一下别随机9字节,可以看出只要是9字节就行,并且前两字节是啥都可以:
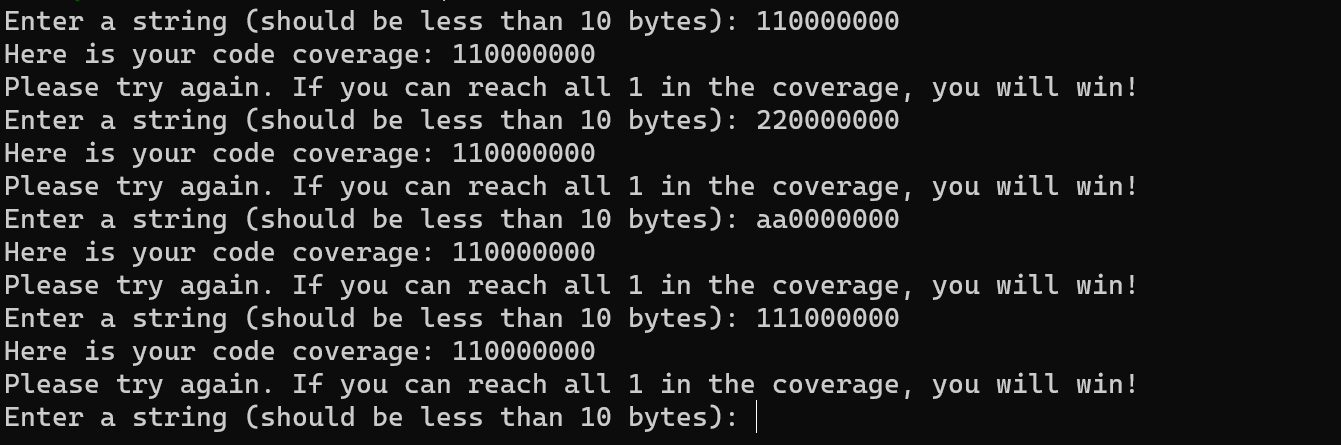
结合比赛继续猜一下后面字节:

可以看到qwb正确了,因此只要fuzz一下后面四字节就行,写个脚本,在测试的时候发现最后一个字节是d:
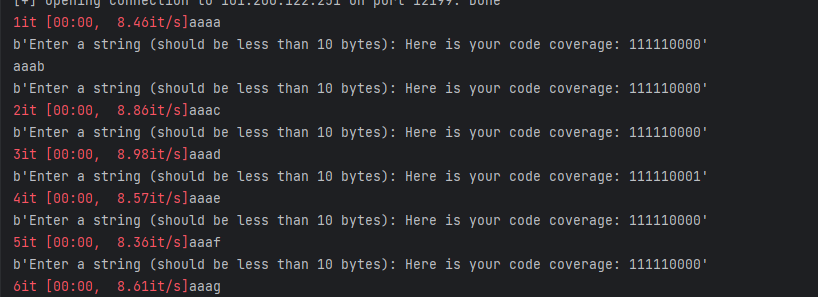
那么只需要fuzz3字节:
from pwn import *
import string
import itertools
from tqdm import tqdm
table = string.ascii_letters
r = remote('101.200.122.251',12188)
pre = '11qwb'
for i in tqdm(itertools.product(table,repeat = 3)):
tail = ''.join(i)
x = (pre + tail + 'd').encode()
r.sendline(x)
f = r.recvline().strip()
if f[-9:] == b'111111111':
print(f)
print(r.recvline())
r.recvline()
谍影重重2
根据题目描述“妄图通过分析参数找到我国飞的最快的飞机”等信息去搜索找到文章 ADS-B系统的工作原理和技术简介 - 简书 (jianshu.com)
进一步搜索找到和ads-b协议有关的内容:
https://mode-s.org/decode/content/ads-b/1-basics.html
gnuradio |民航ADS-B信号仿真分析 - 知乎 (zhihu.com)
主要是需要分析ads-b协议的内容,可以看到该协议前八个比特是固定值hex 0x8d,根据这个特点去分析tcp流量
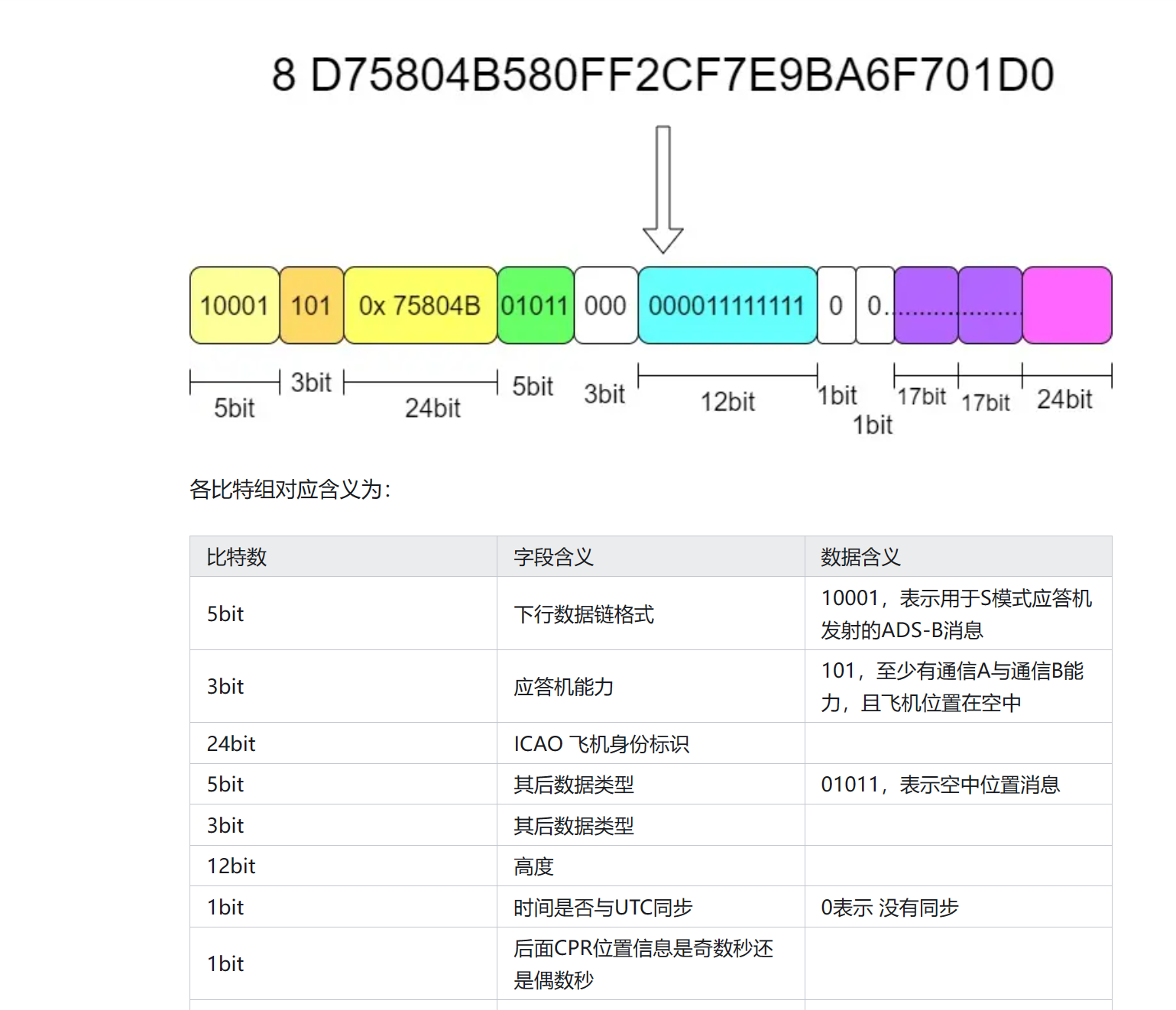
发现无法追踪流,这应该是因为载荷太短了,因此写个脚本提取一下载荷,并把0x8d开头的筛选出来。最后用PyModeS库的tell方法打印飞行数据:
from scapy.all import *
from binascii import hexlify
from pyModeS import tell
payload_list = []
def extract_tcp_payloads(pcap_file):
packets = rdpcap(pcap_file)
for packet in packets:
if 'TCP' in packet and Raw in packet:
tcp_payload = packet[Raw].load
payload_list.append(hexlify(tcp_payload)[18:].decode())
return payload_list
pcap_file = "attach.pcapng"
a = extract_tcp_payloads(pcap_file)
f = open('secrets.txt','w')
for i in a:
if i[:2] == '8d':
tell(i)
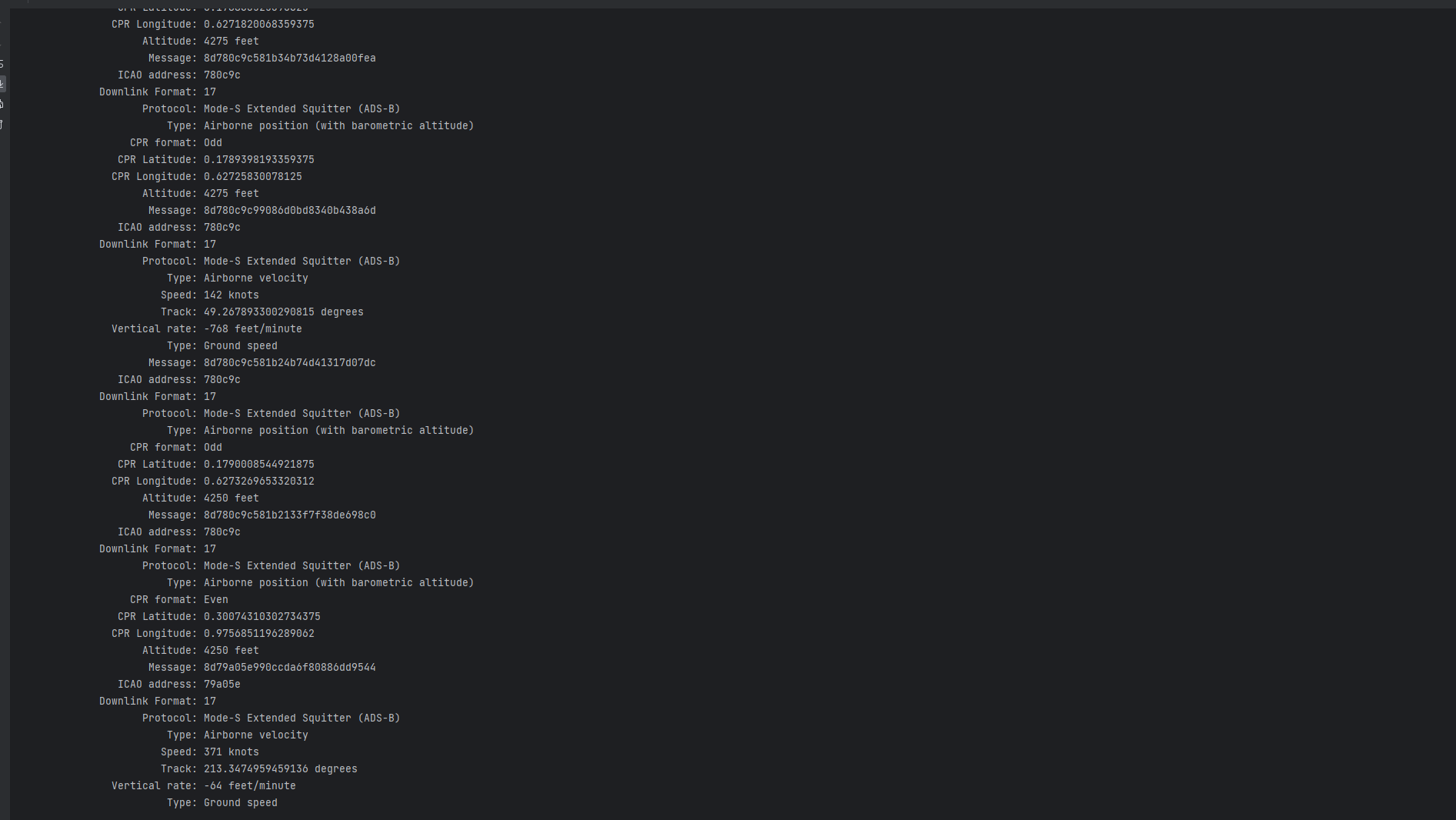
找到speed最大的飞机编号为79A05E,转一下md5即可。
谍影重重3
根据题目描述,隧道、纸飞机等描述猜测是Shad0wsocks的流量。
直接搜索可以找到一篇相关文章:
首先本题给的流量是tcp,那么直接去分析tcprelay.py,他调用了encrypt.py等几个包。因为是隧道技术,保证数据机密性很重要,因此主要分析加密部分encrypt.py:
用以下代码进行初始化:
def get_cipher(self, password, method, op, iv):
password = common.to_bytes(password)
m = self._method_info
if m[METHOD_INFO_KEY_LEN] > 0:
key, _ = EVP_BytesToKey(password,
m[METHOD_INFO_KEY_LEN],
m[METHOD_INFO_IV_LEN])
else:
# key_length == 0 indicates we should use the key directly
key, iv = password, b''
self.key = key
iv = iv[:m[METHOD_INFO_IV_LEN]]
if op == CIPHER_ENC_ENCRYPTION:
# this iv is for cipher not decipher
self.cipher_iv = iv
return m[METHOD_INFO_CRYPTO](method, key, iv, op, self.crypto_path)
可以看到key的生成是调用了EVP_BytesToKey,那么分析EVP_BytesToKey函数:
def EVP_BytesToKey(password, key_len, iv_len):
# equivalent to OpenSSL's EVP_BytesToKey() with count 1
# so that we make the same key and iv as nodejs version
cached_key = '%s-%d-%d' % (password, key_len, iv_len)
r = cached_keys.get(cached_key, None)
if r:
return r
m = []
i = 0
while len(b''.join(m)) < (key_len + iv_len):
md5 = hashlib.md5()
data = password
if i > 0:
data = m[i - 1] + password
md5.update(data)
m.append(md5.digest())
i += 1
ms = b''.join(m)
key = ms[:key_len]
iv = ms[key_len:key_len + iv_len]
cached_keys[cached_key] = (key, iv)
return key, iv
其实就是用passwd作为种子, 根据key的长度来不断哈希来生成真正的key
可以看到该函数生成的iv是没用的,所以源码里用_表示。
最后分析一下tcp的payload结构:
因此追踪流iv已知,只差一个key,可以考虑去爆破一下key,因为没有别的信息
提取出来的payload数据是e0a77dfafb6948728ef45033116b34fc855e7ac8570caed829ca9b4c32c2f6f79184e333445c6027e18a6b53253dca03c6c464b8289cb7a16aa1766e6a0325ee842f9a766b81039fe50c5da12dfaa89eacce17b11ba9748899b49b071851040245fa5ea1312180def3d7c0f5af6973433544a8a342e8fcd2b1759086ead124e39a8b3e2f6dc5d56ad7e8548569eae98ec363f87930d4af80e984d0103036a91be4ad76f0cfb00206
iv长度为16字节固定。即前32位是iv:e0a77dfafb6948728ef45033116b34fc
找了个常用字典进行生成key爆破,然后用解密的值decode确定key为superman,且拿到文件名,文件名是Why-do-you-want-to-know-what-this-is

exp:
import hashlib
import binascii
ciphertext = binascii.unhexlify('855e7ac8570caed829ca9b4c32c2f6f79184e333445c6027e18a6b53253dca03c6c464b8289cb7a16aa1766e6a0325ee842f9a766b81039fe50c5da12dfaa89eacce17b11ba9748899b49b071851040245fa5ea1312180def3d7c0f5af6973433544a8a342e8fcd2b1759086ead124e39a8b3e2f6dc5d56ad7e8548569eae98ec363f87930d4af80e984d0103036a91be4ad76f0cfb00206')
def decrypt(ciphertext, key, iv):
cipher = AES.new(key, AES.MODE_CFB, iv, segment_size=128)
plaintext = cipher.decrypt(ciphertext)
return plaintext
def EVP_BytesToKey(password, key_len, iv_len):
# equivalent to OpenSSL's EVP_BytesToKey() with count 1
# so that we make the same key and iv as nodejs version
m = []
i = 0
while len(b''.join(m)) < (key_len + iv_len):
md5 = hashlib.md5()
data = password
if i > 0:
data = m[i - 1] + password
md5.update(data)
m.append(md5.digest())
i += 1
ms = b''.join(m)
key = ms[:key_len]
iv = ms[key_len:key_len + iv_len]
return key, iv
from Crypto.Cipher import AES
f = open('top.txt','r')
for i in f.readlines():
k = i.strip().encode()
key,iv=EVP_BytesToKey(k,32,16)
iv = binascii.unhexlify('e0a77dfafb6948728ef45033116b34fc')
try:
m = decrypt(ciphertext,key,iv).decode()
print(m)
except:
continue
Wabby Wabbo Radio
F12看下network,然后点播放键会去访问play接口然后生成wav文件:
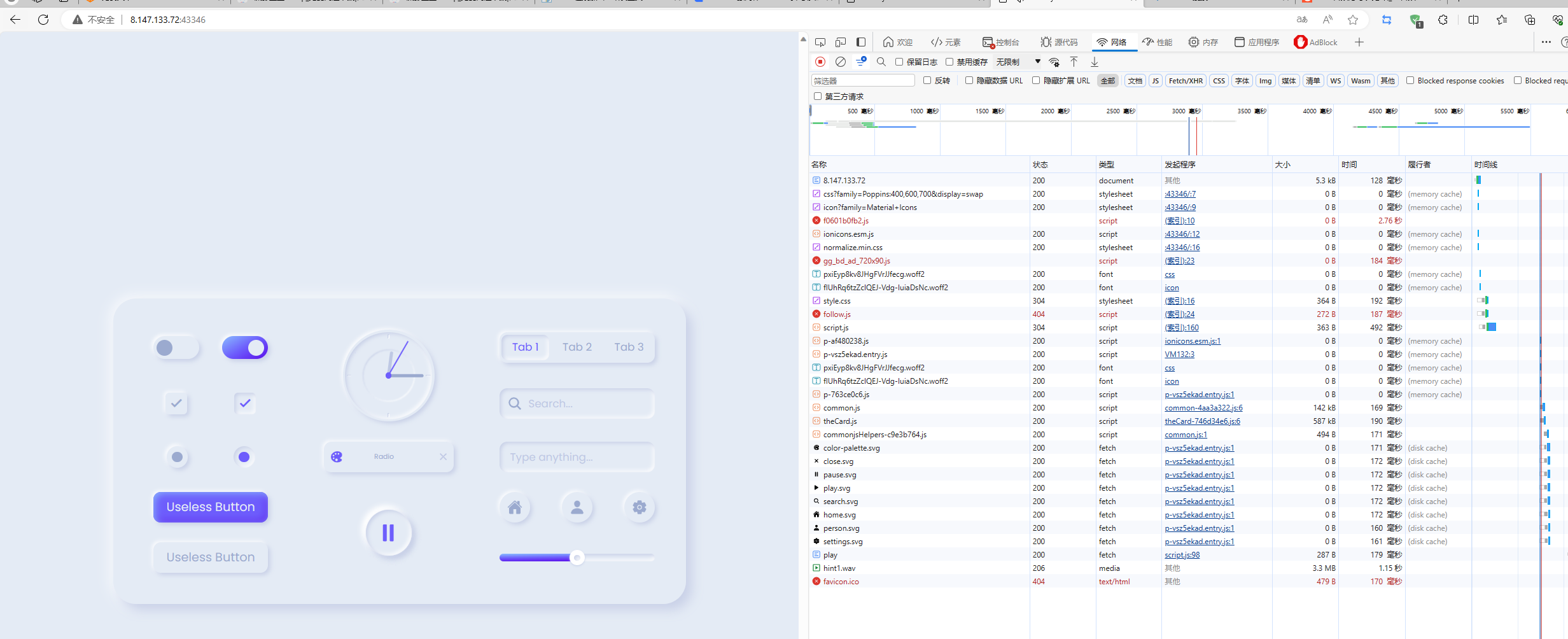
通过这样的方式可以拿到flag.wav,hint1.wav,hint2.wav,还有些xh1.wav等文件。
听一下音频,hint1和hint2都有明显的莫斯密码节奏,flag.wav听不出是啥先不管。
hint1在AU里面分离一下声道,下面就是莫斯电码了,转一下得到:DOYOUKNOWQAM?
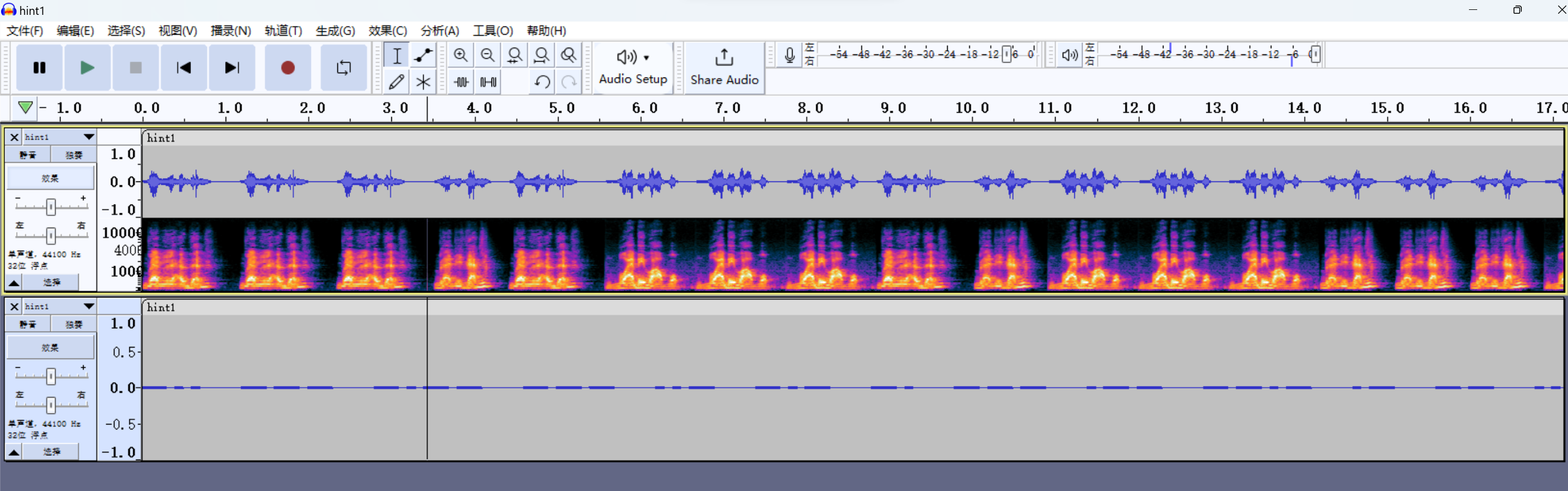
hint2多视图+分离声道得到另一个莫斯:MAYBEFLAGISPNGPICTURE
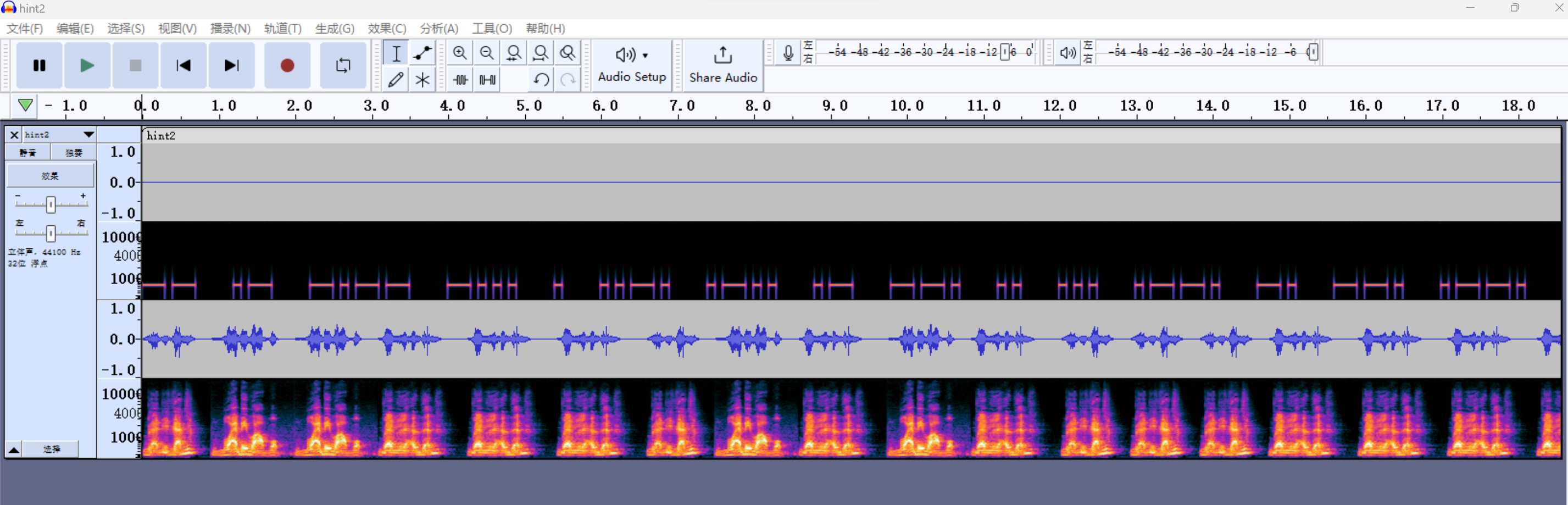
两个hint一个提示我们QAM,另一个告诉我们flag是png图片。xh系列图片同样可以转莫斯提取字符串,但感觉没啥用处。
搜索一下qam的调制解调脚本可以找到如下内容:
16qam调制解调 python - CSDN文库
16QAM调制和解调 python_mob649e8162842c的技术博客_51CTO博客
可以看到解调是需要用到wav的symbols的

因此要先去找一下怎么读取wav文件的symbols:
语音信号处理——Python如何读取wav文件 - 知乎 (zhihu.com)
可以找到代码:
import scipy.io.wavfile as wav
import matplotlib.pyplot as plt
rt, wavsignal = wav.read('test.wav')
print("sampling rate = {} Hz, length = {} samples, channels = {}, dtype = {}".format(rt, *wavsignal.shape, wavsignal.dtype))
fg=plt.figure(1)
plt.plot(wavsignal)
plt.show()
直接对flag.wav进行解调可以得到二进制序列,cyberchef转一下字节发现没啥规律可言,也不是图片:
import numpy as np
import scipy.io.wavfile as wav
import matplotlib.pyplot as plt
rt, wavsignal = wav.read('flag (1).wav')
print("sampling rate = {} Hz, length = {} samples, channels = {}, dtype = {}".format(rt, *wavsignal.shape, wavsignal.dtype))
# fg=plt.figure(1)
# plt.plot(wavsignal)
# plt.show()
print(wavsignal)
constellation = {
0: (-3, 3),
1: (-1, 3),
2: (1, 3),
3: (3, 3),
4: (-3, 1),
5: (-1, 1),
6: (1, 1),
7: (3, 1),
8: (-3, -1),
9: (-1, -1),
10: (1, -1),
11: (3, -1),
12: (-3, -3),
13: (-1, -3),
14: (1, -3),
15: (3, -3)
}
def qam16_modulation(bits):
symbols = []
for i in range(0, len(bits), 4):
index = int(bits[i:i+4], 2)
symbols.append(constellation[index])
return symbols
def qam16_demodulation(symbols):
bits = ""
for symbol in symbols:
index = min(constellation, key=lambda x: np.abs(constellation[x][0] - symbol[0]) + np.abs(constellation[x][1] - symbol[1]))
bits += format(index, '04b')
return bits
decoded_bits = qam16_demodulation(wavsignal)
print(decoded_bits)
因此要考虑修改一下原脚本,在网上搜索到的qam星座图路径大概都是S形曲线,因此可以把起始点分别换在四个角落,分别画折线对应星座表,发现生成的数据同样也是乱码。于是考虑一些其他的情况,比如直上直下的平行线,左右的平行线,试了几个最终在从下向上的直线这样的星座图得到png文件(将解调的序列用cyber转为字节),即flag图片:
解调生成二进制序列的exp:
import numpy as np
import scipy.io.wavfile as wav
import matplotlib.pyplot as plt
rt, wavsignal = wav.read('flag (1).wav')
print("sampling rate = {} Hz, length = {} samples, channels = {}, dtype = {}".format(rt, *wavsignal.shape, wavsignal.dtype))
# fg=plt.figure(1)
# plt.plot(wavsignal)
# plt.show()
print(wavsignal)
# 星座图对应的关系
constellation = {
0: (-3, -3),
1: (-3, -1),
2: (-3, 1),
3: (-3, 3),
4: (-1, -3),
5: (-1, -1),
6: (-1, 1),
7: (-1, 3),
8: (1, -3),
9: (1, -1),
10: (1, 1),
11: (1, 3),
12: (3, -3),
13: (3, -1),
14: (3, 1),
15: (3, 3)
}
def qam16_modulation(bits):
symbols = []
for i in range(0, len(bits), 4):
index = int(bits[i:i+4], 2)
symbols.append(constellation[index])
return symbols
def qam16_demodulation(symbols):
bits = ""
for symbol in symbols:
index = min(constellation, key=lambda x: np.abs(constellation[x][0] - symbol[0]) + np.abs(constellation[x][1] - symbol[1]))
bits += format(index, '04b')
return bits
decoded_bits = qam16_demodulation(wavsignal)
print(decoded_bits)
Crypto
guess game
非预期直接发1,以极小概率可出。
from pwn import *
token = 'icq8fb5560cd7eede140853cb4e01d75'
while True:
r = remote('47.97.69.130',22333)
#r.interactive()
r.sendline(token.encode())
r.recvuntil(b'>')
r.sendline(b'2')
for i in range(80):
r.recvuntil(b'> ')
r.sendline(b'1')
r.recvline()
flag = r.recvline()
print(flag)
if flag != b'Failed!\n':
print(flag)
exit()
r.close()
not only rsa
factordb查一下表分解n,n=p^5。欧拉函数计算phi发现p-1和e不互素:
from gmpy2 import *
n = 6249734963373034215610144758924910630356277447014258270888329547267471837899275103421406467763122499270790512099702898939814547982931674247240623063334781529511973585977522269522704997379194673181703247780179146749499072297334876619475914747479522310651303344623434565831770309615574478274456549054332451773452773119453059618433160299319070430295124113199473337940505806777950838270849
e = 641747
p = 91027438112295439314606669837102361953591324472804851543344131406676387779969
c = 730024611795626517480532940587152891926416120514706825368440230330259913837764632826884065065554839415540061752397144140563698277864414584568812699048873820551131185796851863064509294123861487954267708318027370912496252338232193619491860340395824180108335802813022066531232025997349683725357024257420090981323217296019482516072036780365510855555146547481407283231721904830868033930943
phi = p**4 * (p-1)
g = gcd(phi,e)
print(g)
# 641747
所以考虑AMM算法,找到一个比较好的参考文章附有代码:
宸极实验室—『CTF』AMM 算法详解与应用 - 知乎 (zhihu.com)
但由于本题n=p^5的特殊性,需要魔改一下AMM算法。
原脚本是对p进行AMM运算,并且p-1为欧拉函数去求(p-1)//e的子群的非原根,我直接将AMM的参数传为n,然后修改了欧拉函数,跑脚本就直接出了:

exp:
from Crypto.Util.number import *
import gmpy2
import time
import random
from tqdm import tqdm
n = 6249734963373034215610144758924910630356277447014258270888329547267471837899275103421406467763122499270790512099702898939814547982931674247240623063334781529511973585977522269522704997379194673181703247780179146749499072297334876619475914747479522310651303344623434565831770309615574478274456549054332451773452773119453059618433160299319070430295124113199473337940505806777950838270849
e = 641747
c = 730024611795626517480532940587152891926416120514706825368440230330259913837764632826884065065554839415540061752397144140563698277864414584568812699048873820551131185796851863064509294123861487954267708318027370912496252338232193619491860340395824180108335802813022066531232025997349683725357024257420090981323217296019482516072036780365510855555146547481407283231721904830868033930943
# p = 91027438112295439314606669837102361953591324472804851543344131406676387779969
def AMM(o, r, q):
start = time.time()
g = Zmod(q)
o = g(o)
# p=g(ZZ(pow(randint(1,n),e,n)))
# while p ^ (euler_phi(q) // r) == 1:
# p=g(ZZ(pow(randint(1,n),e,n)))
p=4145258551260692721052305431639130530578945760244546113028204051107256451801271159761727294660340177714278487398464927586089574009946611876973923081680766565802782975375820231485225265668149950890021216201956552423777768375889191598226010312455976611468626191885937889593045530038408573253571633888483415361151281176537322361990053769652217613469937980284629670106823040153630837680659
p=g(p)
print('[+] Find p:{}'.format(p))
t = 0
s = euler_phi(q)
while s % r == 0:
t += 1
s = s // r
print('[+] Find s:{}, t:{}'.format(s, t))
k = 1
while (k * s + 1) % r != 0:
k += 1
alp = (k * s + 1) // r
print('[+] Find alp:{}'.format(alp))
a = p ^ (r**(t-1) * s)
b = o ^ (r*alp - 1)
c = p ^ s
h = 1
for i in range(1, t):
d = b ^ (r^(t-1-i))
if d == 1:
j = 0
else:
print('[+] Calculating DLP...')
j = - discrete_log(d, a)
print('[+] Finish DLP...')
b = b * (c^r)^j
h = h * c^j
c = c^r
result = o^alp * h
end = time.time()
print("Finished in {} seconds.".format(end - start))
print('Find one solution: {}'.format(result))
return result
def onemod(p,r):
t=p-2
s = euler_phi(p)
while pow(t,s // r,p)==1:
t -= 1
return pow(t,s // r,p)
def solution(p,root,e):
g = onemod(p,e)
may = set()
for i in range(e):
may.add(root * pow(g,i,p)%p)
return may
def union(x1, x2):
a1, m1 = x1
a2, m2 = x2
d = gmpy2.gcd(m1, m2)
assert (a2 - a1) % d == 0
p1,p2 = m1 // d,m2 // d
_,l1,l2 = gmpy2.gcdext(p1,p2)
k = -((a1 - a2) // d) * l1
lcm = gmpy2.lcm(m1,m2)
ans = (a1 + k * m1) % lcm
return ans,lcm
def excrt(ai,mi):
tmp = zip(ai,mi)
return reduce(union, tmp)
mp = AMM(c,e,n)
print(mp)
mps = solution(n,mp,e)
for mpp in tqdm(mps):
# print(mpp)
assert ZZ(pow(mpp,e,n))==c
flag = long_to_bytes(int(mpp))
if b'flag' in flag:
print(flag)
exit(0)
另一个思路是直接用nth_root,它里面有lifting操作。
from Crypto.Util.number import *
n = 6249734963373034215610144758924910630356277447014258270888329547267471837899275103421406467763122499270790512099702898939814547982931674247240623063334781529511973585977522269522704997379194673181703247780179146749499072297334876619475914747479522310651303344623434565831770309615574478274456549054332451773452773119453059618433160299319070430295124113199473337940505806777950838270849
e = 641747
c = 730024611795626517480532940587152891926416120514706825368440230330259913837764632826884065065554839415540061752397144140563698277864414584568812699048873820551131185796851863064509294123861487954267708318027370912496252338232193619491860340395824180108335802813022066531232025997349683725357024257420090981323217296019482516072036780365510855555146547481407283231721904830868033930943
c = Mod(c,n)
tmp = c.nth_root(e,all=True)
for t in tmp:
if b"flag{" in long_to_bytes(t):
print(long_to_bytes(t))
补一个标准的amm + hensel lifting:
import random
import math
import libnum
import time
from Crypto.Util.number import bytes_to_long,long_to_bytes
p = 0
#设置模数
def GF(a):
global p
p = a
#乘法取模
def g(a,b):
global p
return pow(a,b,p)
def AMM(x,e,p):
GF(p)
y = random.randint(1, p-1)
while g(y, (p-1)//e) == 1:
y = random.randint(1, p-1)
print(y)
print("find")
#p-1 = e^t*s
t = 1
s = 0
while p % e == 0:
t += 1
print(t)
s = p // (e**t)
print('e',e)
print('p',p)
print('s',s)
print('t',t)
# s|ralpha-1
k = 1
while((s * k + 1) % e != 0):
k += 1
alpha = (s * k + 1) // e
#计算a = y^s b = x^s h =1
#h为e次非剩余部分的积
a = g(y, (e ** (t - 1) ) * s)
b = g(x, e * alpha - 1)
c = g(y, s)
h = 1
#
for i in range(1, t-1):
d = g(b,e**(t-1-i))
if d == 1:
j = 0
else:
j = -math.log(d,a)
b = b * (g(g(c, e), j))
h = h * g(c, j)
c = g(c, e)
#return (g(x, alpha * h)) % p
root = (g(x, alpha * h)) % p
roots = set()
for i in range(e):
mp2 = root * g(a,i) %p
assert(g(mp2, e) == x)
roots.add(mp2)
return roots
n = 6249734963373034215610144758924910630356277447014258270888329547267471837899275103421406467763122499270790512099702898939814547982931674247240623063334781529511973585977522269522704997379194673181703247780179146749499072297334876619475914747479522310651303344623434565831770309615574478274456549054332451773452773119453059618433160299319070430295124113199473337940505806777950838270849
e = 641747
p = 91027438112295439314606669837102361953591324472804851543344131406676387779969
c = 730024611795626517480532940587152891926416120514706825368440230330259913837764632826884065065554839415540061752397144140563698277864414584568812699048873820551131185796851863064509294123861487954267708318027370912496252338232193619491860340395824180108335802813022066531232025997349683725357024257420090981323217296019482516072036780365510855555146547481407283231721904830868033930943
cp = c % p
mps = AMM(cp,e,p)
print('AMM done')
from Crypto.Util.number import *
from gmpy2 import *
import random
from tqdm import *
e = 641747
c = 730024611795626517480532940587152891926416120514706825368440230330259913837764632826884065065554839415540061752397144140563698277864414584568812699048873820551131185796851863064509294123861487954267708318027370912496252338232193619491860340395824180108335802813022066531232025997349683725357024257420090981323217296019482516072036780365510855555146547481407283231721904830868033930943
phi = p ** 4 * (p - 1)
# hensel lifting
b = 5
for m in tqdm(mps):
#print(m)
for i in range(1, b):
_dx = -invert(e*pow(m,(e-1),p**(i+1)),p) % p**(i+1)
mod_temp = (pow(m,e,p**(i+1))-c)//(p**i) % p**(i+1)
t = _dx * mod_temp % p
m = m + p**i*t % (p**(i+1))
#print(m)
if(b"flag{" in long_to_bytes(m)):
print(long_to_bytes(m))
break
discrete_log
Low Hamming Weight DLP,类似于bsgs的思想,需要高性能cpu多核跑。
import sys
import time
from datetime import datetime
from itertools import product
from multiprocessing import Pool
from Crypto.Util.number import *
from Crypto.Util.Padding import pad
from tqdm import tqdm
p = 0xf6e82946a9e7657cebcd14018a314a33c48b80552169f3069923d49c301f8dbfc6a1ca82902fc99a9e8aff92cef927e8695baeba694ad79b309af3b6a190514cb6bfa98bbda651f9dc8f80d8490a47e8b7b22ba32dd5f24fd7ee058b4f6659726b9ac50c8a7f97c3c4a48f830bc2767a15c16fe28a9b9f4ca3949ab6eb2e53c3
g = 5
c = 105956730578629949992232286714779776923846577007389446302378719229216496867835280661431342821159505656015790792811649783966417989318584221840008436316642333656736724414761508478750342102083967959048112859470526771487533503436337125728018422740023680376681927932966058904269005466550073181194896860353202252854 # flag
# c = 113899731239522155857343253779217495886305719179149382710413337730296590467493272877934831949985611142935447847274294380061552428568325157112382258003397585331908810093880351403432402979556351883303784625842063593420814374501431314557706964231378845860401606163097676751056181943537079433290670109490856739247 # fake flag
F = GF(p)
g = F(g)
c = F(c)
l = []
for ch in "0123456789abcdef":
l.append(ord(ch))
start = datetime.now()
print(f"[{datetime.now()}] start...")
for flag_len in range(6+6, 6+17):
print(f"flag_len: {flag_len}")
unknown_bytes_len = flag_len - 6
pad_len = 128 - flag_len
flag_base = "flag{" + "\x00"*(flag_len-6) + "}"
m_base = bytes_to_long(pad(flag_base.encode(), 128))
h = c * g^(-m_base)
a = g^(pow(256, (1 + pad_len)))
half = min(unknown_bytes_len // 2 - 1, 7)
# h == a^x
# h == a^(a1 + a2*256^half), where a1 in [0, 256^half] and a2 in [0, 256^half]
# h * a^(-a2 * 256^half) == a^a1
# h * (a^(-256^half))^a2
# Compute the baby steps and store them in the 'precomputed' hash table.
print(f"[{datetime.now()}] precomputing start: {pow(16,half)}...")
precomputed = {}
for n_bytes in tqdm(product(l, repeat=half)):
a1 = 0
for byte in n_bytes:
a1 = (a1 << 8) + byte
precomputed[a^a1] = a1
print(f"[{datetime.now()}] precomputing end: {len(precomputed)}, {sys.getsizeof(precomputed)}")
# Now compute the giant steps and check the hash table for any matching.
s = a^(-256^half)
def giant_step(first, second):
print(first, second)
# table = precomputed.copy()
for left_bytes in tqdm(product(l, repeat=unknown_bytes_len-half-2)):
try:
a2 = (first << 8) + second
for byte in left_bytes:
a2 = (a2 << 8) + byte
a1 = precomputed[h * s^a2]
except KeyError:
pass
else:
print(a1, a2)
xx = a1 + a2*256^half
print(f"find logarithm: {xx}")
print(f"find logarithm: {xx}")
print(f"find logarithm: {xx}")
return xx
return None
def cb(xx):
if xx:
print(xx)
with open(f"result_{xx}.txt", "w") as f:
f.write(str(xx))
end = datetime.now()
print(f"total time cost: {end - start}")
exit(0)
pool = Pool(256)
for first in l:
for second in l:
pool.apply_async(giant_step, (first, second), callback=cb)
pool.close()
pool.join()
pool.close()


 浙公网安备 33010602011771号
浙公网安备 33010602011771号