“华为杯”第二届中国研究生网络安全创新大赛

初赛，和学弟打了个第二，没做到很难的题目。

一个小秘密

提示说：除了base64还有什么编码 MFZWIYLEMFSA====
尝试base32解密：

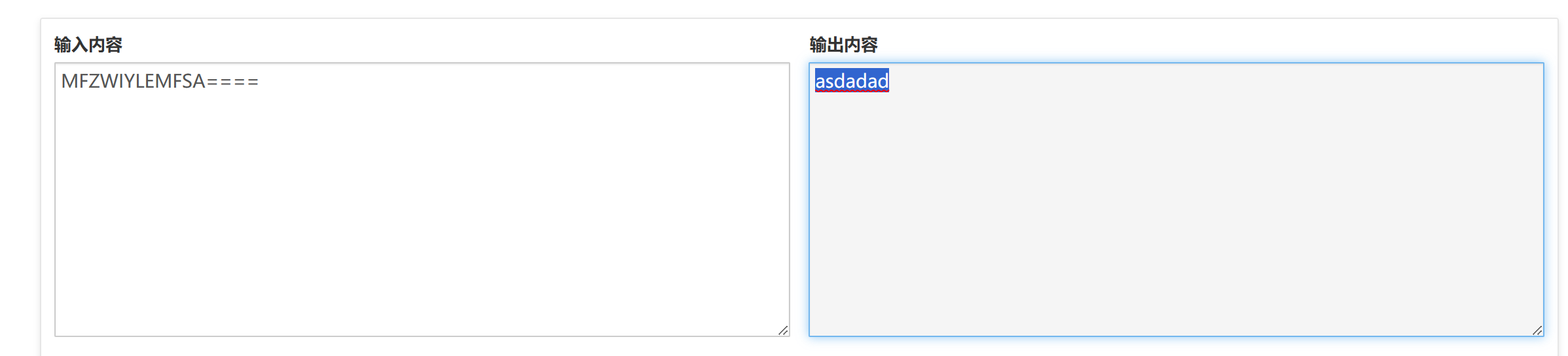
asdadad作为解压密码可以解开压缩包，里面有个txt文件，稍微看一下可以找到PK头，也可以看到xml文件，因此可知是word文件，所以直接改为zip后缀解压，在document.xml里面可以找到一串U2F开头的密文，可以找到这个密文相应的网站，尝试aes解密，再最后解base64即可

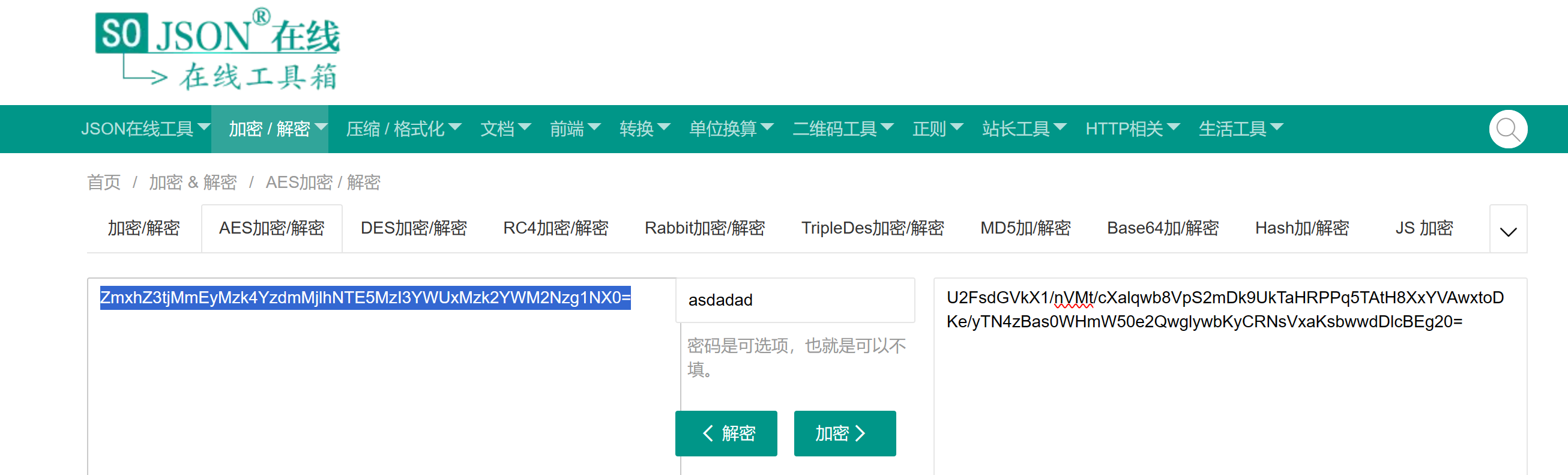
StepBystep

由于y = p ^ (bytes_to_long(part1) << 0x100)，我们已知p的高位和低位比特，只有中间那部分与part1异或的是未知的。而我们知道未知比特长度为32x8，那么方程可建立为:

\[p_{h} \cdot 2^{2^{32}+32*8} +x\cdot 2^{256} + p_{l} \equiv 0\;mod\;n \]

利用coppersmith即可解出x并恢复p。
得到p之后可以通过异或和移位操作还原part1.

2.通过二次剩余判定来还原part2。

def bit_enc(m,n):
    enc = []
    m = bin(bytes_to_long(m))[2:]
    for x in m:
        while True:
            r = random.randint(1, n)
            if GCD(r, k) == 1:
                enc.append((k ** int(x) * r ** 2) % n)
                break
    return enc

函数对m的每一比特进行加密，若比特为0，则返回\(r^2\;mod\;n\)，否则返回\(k.r^2\;mod\;n\)。
因为k是模p的二次非剩余，可以对每一组密文在模p下进行二次剩余判定，若为二次剩余，则说明该密文对应的比特为0，反之成立。对二次剩余的判定，可以利用sage集成的函数kronecker：

for cc in enc1:
    t = cc%p
    if kronecker(t,p) == -1:
        m2 = m2 +'1'
    else:
        m2 = m2 +'0'
m2 = long_to_bytes(int(m2,2))

3.根据题目，有以下关系：

\[M = m\;mod\;r\\ m^3\;mod\;n =enc2 \]

利用其建立coppersmith的方程。设\(m = kr+M\)，有\((kr+M)^3-enc2\equiv0\;mod\;n\)，copper求k再解m即可。

e = 3
kbits = 200
P.<x> = PolynomialRing(Zmod(n))
f = (M + r*x)^e - enc2
f=f.monic() #归一
res = f.small_roots(x=2^kbits,epslon=0.04)
print(res)
xx = res[0]
m3 = M + r*xx
m3 = long_to_bytes(int(m3))[:32]

把三段part拼起来，再base64解密即可。

next-prime

只给了n的高504位，但由于p和q非常接近，并且n的低位对开方影响很小，所以将n左移520位再开方可以得到p和q之间的一个数，那么再减去一个小的值，它的下一个素数多半就是p。

import gmpy2
from Crypto.Util.number import *
from sympy.ntheory import prevprime,nextprime

n= 28576274811010794362153160897556935178530640825011441539841241257190782139295561904323347128956873569754645071205043238985141474388531008367238218822591
c= 49502875285578675438052554215266678403659290915102322948363030271494959804587081871467110614683972929037615883922743651431683465100061968204901334627149795829429950385848753728500177164800064208215503246868631076011505268371936586645321659884527055007299822625570713613996139223348709621258028349513737798120
n = n * 2 ** 520
base = gmpy2.iroot(n,2)[0]

for i in range(100):
    base = prevprime(base)
    q = nextprime(base)
    n = base*q
    phi = (base-1)*(q-1)
    d = inverse(65537,phi)
    m = pow(c,d,n)
    r = long_to_bytes(int(m))
    if b'flag' in r:
        print(r)
        break

EC_Party-I

对n的分解可以用类似于Elliptic Curve Factorization Method的思路，整数因子分解 - maTHμ - 计算机代数系统 (mathmu.github.io)。具体来说可以参考hitcon2022的Chimera这题，将order的一个小因子除掉再乘以E(C)，可能会产生kp mod n的情况，这会让sagemath报错，我们得以看到kp的值：

后边就是ecrsa的求解，2与Fq的order oq互素，因此可以求出Fq下的m，但2与Fp的order op不互素，可以通过解方程得到Fp下的m，最后crt即可。

from Crypto.Util.number import *

a,b,n,C = 138681122158674534796479818810828100269024674330030901179877002756402543027343312824423418859769980312713625658733, 4989541340743108588577899263469059346332852532421276369038720203527706762720292559751463880310075002363945271507040, 762981334990685089884160169295988791471426441106522959345412318178660817286272606245181160960267776171409174142433857335352402619564485470678152764621235882232914864951345067231483720755544188962798600739631026707678945887174897543, (19591102741441427006422487362547101973286873135330241799412389205281057650306427438686318050682578531286702107543065985988634367524715153650482199099194389191525898366546842016339136884277515665890331906261550080128989942048438965, 728465071542637655949094554469510039681717865811604984652385614821789556549826602178972137405550902004858456181137844771163710123158955524137202319902378503104952106036911634918189377295743976966073577013775200078470659428344462772)
E = EllipticCurve(Zmod(n),[a,b])
C = E(C)
order = 762981334990685089884160169295988791471426441106522959345445792076415993922016249232021560266153453470937452118572318136597282436269660557904217923887981072203978473274822142705255987334355747997513083011853917049784914749699536828

#fac
o = order // 8452217
#print(C*o)
# for i in range(1,10000):
#     tt = (order//i)*C

p = 37474009785980474658135106783131904659818035950984079581009709986840194575036321428945132957079423328996508289872067
q = n//p
assert p*q == n
Ep = EllipticCurve(Zmod(p),[a,b])
Eq = EllipticCurve(Zmod(q),[a,b])
#print(Ep.order())
#print(Eq.order())
op = 37474009785980474658135106783131904659818035950984079581012533947688268013671227793391417023914911897089093262951596
oq = order // op
dq = inverse_mod(2,oq)
mq = dq*Eq(C)

print(Ep(C))
R.<x> = PolynomialRing(GF(p))
f = (3*x^2+a)^2-2*x*(4*(x^3+a*x+b))-C[0]*4*(x^3+a*x+b)

for i in (f.roots()):
    print(long_to_bytes(crt([int(i[0]),int(mq[0])],[p,q])))
print('done')