NCTF 2022
南邮的比赛,主要做了misc,密码到时候复现一下后两题。
Misc
Signin
无壳exe,idapro反编译直接定位到flag位置,发现是一堆字符构成的,于是写个脚本按照原样输出,根据大致形状和语义可以得到flag:
c =[ " _ _ ___ _____ ___ /\"/ __ __ __ __ _ __ __"
"__ _____ __ _ _ ___ _____ ___ ___ __ ___ "
"___ _ _ _ \\\"\\ \n"
" | \\| | / __| |_ _| | __| _| | \\ \\ / / \\ \\ / / ___ / | __ / \\ _ __ "
" |__ / |_ _| / \\ | \\| | / __| |_ _| | __| |_ ) / \\ |"
"_ ) |_ ) | | | | | | | |_ \n"
" | .` | | (__ | | | _| | | \\ V / \\ V / / -_) | | / _| | () | | ' \\ "
"|_ \\ ___ | | | () | ___ | .` | | (__ | | | _| ___ / / | () | / / "
" / / |_| |_| |_| | | \n"
" |_|\\_| \\___| _|_|_ _|_|_ _\\_\\_ _\\_/_ _\\_/_ \\___| _|_|_ \\__|_ _\\__/ |_|_"
"|_| |___/ |___| _|_|_ _\\__/ |___| |_|\\_| \\___| _|_|_ _|_|_ |___| /___| _\\__/"
" /___| /___| _(_)_ _(_)_ _(_)_ /_/__ \n"
"_|\"\"\"\"\"|_|\"\"\"\"\"|_|\"\"\"\"\"|_| \"\"\" |_|\"\"\"\"\"|_| \"\"\"\"|_| \"\"\"\"|_|\"\"\"\"\"|_|"
"\"\"\"\"\"|_|\"\"\"\"\"|_|\"\"\"\"\"|_|\"\"\"\"\"|_|\"\"\"\"\"|_|\"\"\"\"\"|_|\"\"\"\"\"|_|\"\"\"\"\"|"
"_|\"\"\"\"\"|_|\"\"\"\"\"|_|\"\"\"\"\"|_|\"\"\"\"\"|_| \"\"\" |_|\"\"\"\"\"|_|\"\"\"\"\"|_|\"\"\"\"\"|"
"_|\"\"\"\"\"|_|\"\"\"\"\"|_| \"\"\" |_| \"\"\" |_| \"\"\" |_|\"\"\"\"\"| \n"
"\"`-0-0-'\"`-0-0-'\"`-0-0-'\"`-0-0-'\"`-0-0-'\"`-0-0-'\"`-0-0-'\"`-0-0-'\"`-0-0-'\"`-0-0-'\"`-0-0-'\"`"
"-0-0-'\"`-0-0-'\"`-0-0-'\"`-0-0-'\"`-0-0-'\"`-0-0-'\"`-0-0-'\"`-0-0-'\"`-0-0-'\"`-0-0-'\"`-0-0-'\"`-0-"
"0-'\"`-0-0-'\"`-0-0-'\"`-0-0-'\"`-0-0-'\"`-0-0-'\"`-0-0-'\"`-0-0-' \n"]
for i in c:
print(i)
#NCTF{VVe1c0m3_T0_NCTF_2022!!!}
只因因
把第二个基因片段拿去搜索就能得到如下结果,把CFTR做一个md5包上NCTF{}即可。
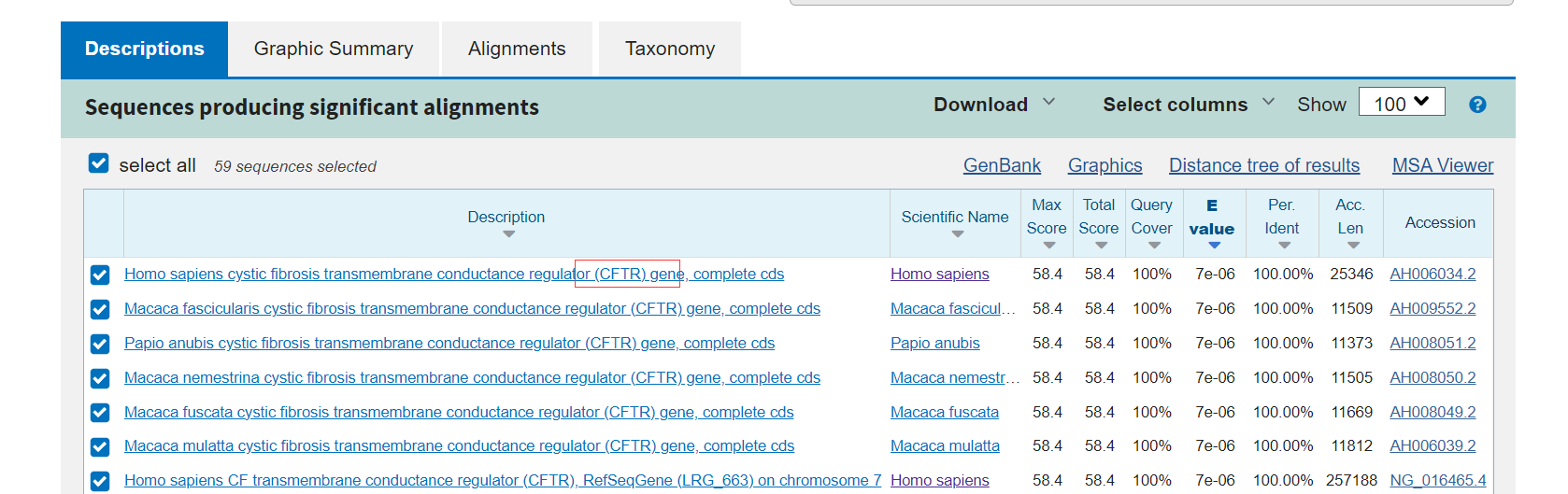
炉边聚会
一开始以为把炉石卡组代码拿去解析看牌就行,结果没有flag。然后找到一篇关于卡组代码结构的博客. 重点其实就在于 varint 编码编码这个地方,只要能够实现 varint 解析就差不多搞定了,参考博客的意思写了一个:
def parseVarint(data):
shift =0
res = 0
while True:
temp = data.pop(0)
res |= (temp & 0x7f) << shift
shift += 7
if (temp & 0x80) == 0:
break
#print(result)
return res
测试了一下发现,每次放进去的data应该是去掉第一个元素的数组,遂解析成功,发现了1230,1250等数字,这还比较明显,去掉最后一位转ascii字符即可。完整exp:
import base64
c = 'AAEDAZoFKIwGngXIBrwFzgnQBfIHygf0CIgJkAi+BogJ1gjMCPIHtgeeBeAD6AfyB7YHvgbgA+AD4AO2B7wFkgnMCMwI+ga2B/QImgi6BJAIiAn2BOIJAAA='
c1 = list(base64.b64decode(c))
print(c1)
def parseVarint(data):
shift =0
res = 0
while True:
temp = data.pop(0)
res |= (temp & 0x7f) << shift
shift += 7
if (temp & 0x80) == 0:
break
#print(result)
return res
# test data
# ciphey = 'AAECAf0EHk2KAckDqwTLBJYF4QfsB40IvuwCpvACw/gCxvgCtfwCoIAD55UDg5YD05gDvZkDn5sDoJsDip4DpaEDwqED/KMDi6QDkqQDv6QDhKcDn7cDAAA='
# t = list(base64.b64decode(ciphey))
# get flag
for i in range(0,len(c1)):
try :
s = parseVarint(c1[i:])
tmp = str(s)[:-1]
print(chr(int(tmp)),end='')
except:
continue
qrssssssss
应该是非预期,随便扫描了几个二维码,发现都是一个可见字符,那么猜测flag由这些字符组成。我的想法是 如果出题人是一张张生成png的话,一定有时间先后顺序,正好大致是flag的顺序。那么就按照png的修改时间进行排序,再扫描就能得到大致flag。这部分的exp:
import os
dir_name = "./"
file_list = os.listdir(dir_name)
# 获取按照文件时间创建排序的列表,默认是按时间升序
new_file_list = sorted(file_list, key=lambda file: os.path.getmtime(os.path.join(dir_name, file)))
print(new_file_list)
from PIL import Image
import pyzbar.pyzbar as pyzbar
def QRcode_message(image):
img = Image.open(image) # 读取图片
# 因为一张图片可能是一张二维码,也可能里面有许多二维码
barcodes = pyzbar.decode(img) # 解析图片信息
for barcode in barcodes:
# 如果图片有多个二维吗信息,会自动循环解析
barcodeData = barcode.data.decode("utf-8")
return barcodeData
import os
f = open('out_time.txt','w')
txts = []
for name in new_file_list: #遍历文件夹
position = name
tmp = str(QRcode_message(position))
f.write(tmp)
输出为NNNNNNNNNNNNNNNNCTTTCCTTFTCTFFFCTCTCCCFFCFFCCTFTCTFCTFFFFFTCTTFC{77{{7{{{{{7{77{7{{{777777{7{7{73333333333333333777777777777777711111111111111115555555555555555--00----00--0--0-00-0-00---00000eeeeeeeeeeeeeeeeebeebeebeebebbbebebebebeebeebbbb----------------444444444444444465655565555665666666565655566655----------------99ee9eee9ee99ee9e99e99e999eee99e1111111111111111----------------111111111111111111111111111111110000000000000000aa8aa8a8a8aa88a8aa8a8a8888a8a88affffffffffffffffbbbbbbbbbbbbbbbb}}}}}}}}}}}}}}}}
根据题目描述,大概判断是重复16次的字符为flag的一个字符,那么先确定比较明显的,不确定顺序的几个地方进行爆破 多次提交即可:
c = 'NCTF{737150-ebe-465-9e1-110a8fb}'
possible1 = ['be','eb']
possible2 = ['65','56']
possible3 = ['e9','9e']
possible4 = ['a8','8a']
for i1 in possible1:
for i2 in possible2:
for i3 in possible3:
for i4 in possible4:
m = 'NCTF{737150-' + 'e' + i1 + '-4' + i2 + '-' + i3 + '1-' + '110' + i4 + 'fb}'
print(m)
# NCTF{737150-eeb-465-e91-110a8fb}
qrssssssss_revenge
预期解是利用纠错码等级LMQH(0-9)来排序的,相关知识可参考QR码参考资料,出题人的wp是利用qrazybox来手动提取右上角的掩码信息,再用该信息对照图片进行排序,虽然实现了自动处理但是在原理方面没讲太清楚。我认为好的解法应该是要去识别二维码左上方的纠错等级和掩码类别(000-111),根据这5个bit就能确定二维码的顺序,按照顺序拼接码中信息即可。具体地,按照01000-10111构造一个列表,然后把每张图的纠错等级掩码类别5个bit和10101进行异或(因为二维码的这5个bit是异或10101得到的,要得到原本的值需要异或回去),异或的结果在列表中查找index再替换字符即可。

from PIL import Image
import cv2
from pyzbar import pyzbar
import os
from tqdm import tqdm
xor_mask = int('10101',2)
# 题目给了flag的括号内容为26个字符
flag_list = ['*']*32
def getmask(image):
mask_l = ['01000','01001','01010','01011','01100','01101','01110','01111']
mask_m = ['00000','00001','00010','00011','00100','00101','00110','00111']
mask_q = ['11000','11001','11010','11011','11100','11101','11110','11111']
mask_h = ['10000','10001','10010','10011','10100','10101','10110','10111']
mask_list = mask_l + mask_m + mask_q + mask_h
#print(mask_list)
mask_list_new = []
for i in mask_list:
mask_list_new.append(int(i,2))
img = Image.open(image)
qrcode = cv2.imread(image)
data = pyzbar.decode(qrcode)
text = data[0].data.decode('utf-8')
check = ''
BLOCK = block_size * 8
#print(width-BLOCK)
img = img.crop((0,BLOCK,block_size*5,BLOCK+20)) #截取左上角码块的掩码
for i in range(0,block_size*5,block_size):
n = img.getpixel((i+(block_size//2),block_size//2))
if n == 255:
check += "1"
else:
check += '0'
sign = int(check,2) ^ xor_mask
index_ = mask_list_new.index(sign)
flag_list[index_] = text
return flag_list
# 找到该路径
os.chdir('./qrssssssss_revenge')
block_size = 20
width,height = 660,660
image_names = []
for i in os.listdir('./'):
image_names.append(i)
print(image_names)
for image in tqdm(image_names):
tmp = getmask(image)
# 按照题意flag是倒序排列的,还需要倒置
flag = ''.join(tmp)[::-1]
print(flag)
Crypto
superecc
由于扭曲爱德华曲线和蒙哥马利曲线及Weierstrass曲线在k域上有很强的同源性质,所以能够把扭曲爱德华曲线映射到蒙哥马利上再进一步转化为Weierstrass,最后由于该Weierstrass曲线的阶是光滑的,用Pohlig-Hellman即可很快求解(一个前提是flag很短)。一些参考资料:扭曲爱德华曲线原论文、论文翻译、官方wp、蒙哥马利曲线简介及映射方法。
from Crypto.Util.number import *
p = 101194790049284589034264952247851014979689350430642214419992564316981817280629
a = 73101304688827564515346974949973801514688319206271902046500036921488731301311
c = 78293161515104296317366169782119919020288033620228629011270781387408756505563
d = 37207943854782934242920295594440274620695938273948375125575487686242348905415
P.<z> = PolynomialRing(Zmod(p))
# 把扭曲爱德华曲线映射到蒙哥马利曲线
aa = a
dd = (d*c^4)%p
J = (2*(aa+dd)*inverse(aa-dd,p))%p
K = (4*inverse(aa-dd,p))%p
A = ((3-J^2)*inverse(3*K^2,p))%p
B = ((2*J^3-9*J)*inverse(27*K^3,p))%p
for i in P(z^3+A*z+B).roots():
alpha = int(i[0])
#print(kronecker(3*alpha^2+A,p))
for j in P(z^2-(3*alpha^2+A)).roots():
s = int(j[0])
s = inverse_mod(s, p)
if J==alpha*3*s%p:
Alpha = alpha
S = s
# 扭曲爱德华映射到 Weierstrass形式(其中经过蒙哥马利转换)
def twist_to_weier(x,y):
v = x*inverse(c,p)%p
w = y*inverse(c,p)%p
assert (aa*v^2+w^2)%p==(1+dd*v^2*w^2)%p
s = (1+w)*inverse_mod(1-w,p)%p
t = s*inverse(v,p)%p
assert (K*t^2)%p==(s^3+J*s^2+s)%p
xW = (3*s+J) * inverse_mod(3*K, p) % p
yW = t * inverse_mod(K, p) % p
assert yW^2 % p == (xW^3+A*xW+B) % p
return (xW,yW)
def weier_to_twist(x,y):
xM=S*(x-Alpha)%p
yM=S*y%p
assert (K*yM^2)%p==(xM^3+J*xM^2+xM)%p
xe = xM*inverse_mod(yM,p)%p
ye = (xM-1)*inverse_mod(xM+1,p)%p
assert (aa*xe^2+ye^2)%p==(1+dd*xe^2*ye^2)%p
xq = xe*c%p
yq = ye*c%p
assert (a*xq^2+yq^2)%p==c^2*(1+d*xq^2*yq^2)
return (xq,yq)
E = EllipticCurve(GF(p), [A, B])
G = twist_to_weier(30539694658216287049186009602647603628954716157157860526895528661673536165645,64972626416868540980868991814580825204126662282378873382506584276702563849986)
Q = twist_to_weier(98194560294138607903211673286210561363390596541458961277934545796708736630623,58504021112693314176230785309962217759011765879155504422231569879170659690008)
G = E(G)
Q = E(Q)
factors, exponents = zip(*factor(E.order()))
primes = [factors[i] ^ exponents[i] for i in range(len(factors))][:-2]
print(primes)
# p-h算法求dlp,flag很短不需要管后两个较大的阶因子
dlogs = []
for fac in primes:
t = int(int(G.order()) // int(fac))
dlog = discrete_log(t*Q,t*G,operation="+")
dlogs += [dlog]
print("factor: "+str(fac)+", Discrete Log: "+str(dlog)) #calculates discrete logarithm for each prime order
flag=crt(dlogs,primes)
print(long_to_bytes(flag))


 浙公网安备 33010602011771号
浙公网安备 33010602011771号