RSA常用模数分解算法总结

常见的大数分解算法原理及实现，随着学习不断补充。

Common_prime

其实就是当两个n有公因子的时候，用gcd(n1,n2)即可。

Pollard_p-1

适用于质因子为光滑质数p，即p-1光滑，主要原理如下：

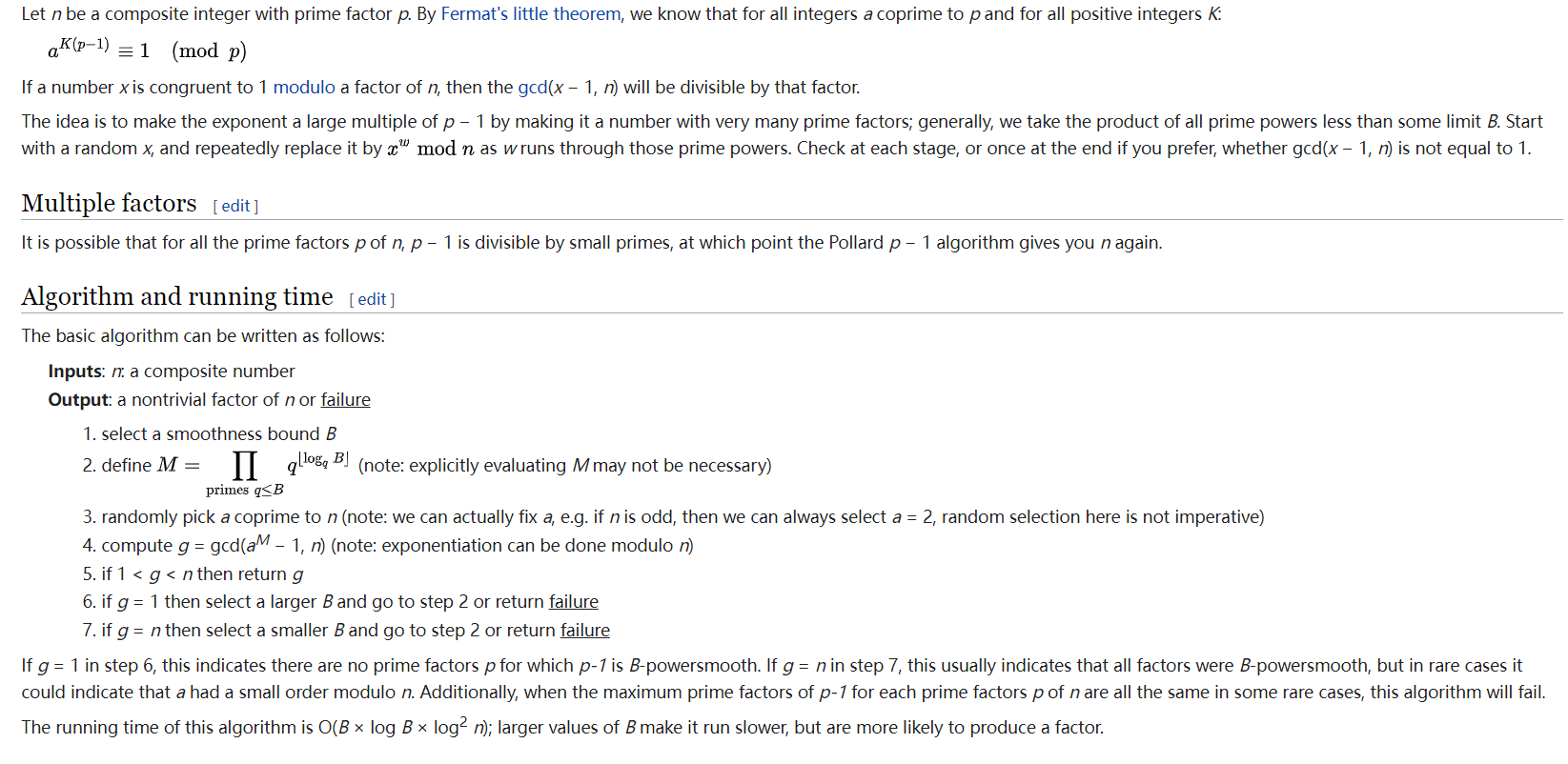
算法实现比较容易，某些时候会出现p-1的因子有一些较大质数的情况，那么需要改写一下原本的算法增大效率，也可以利用集成工具gmp-ecm去分解。primefac实现的pollard_pm1效率不高，并且它一般要求有类似gmp-ecm所需要的上界和次上界，不太好用。

Williams_p+1

类似于p_1算法，但是基于卢卡斯序列来实现，主要原理：

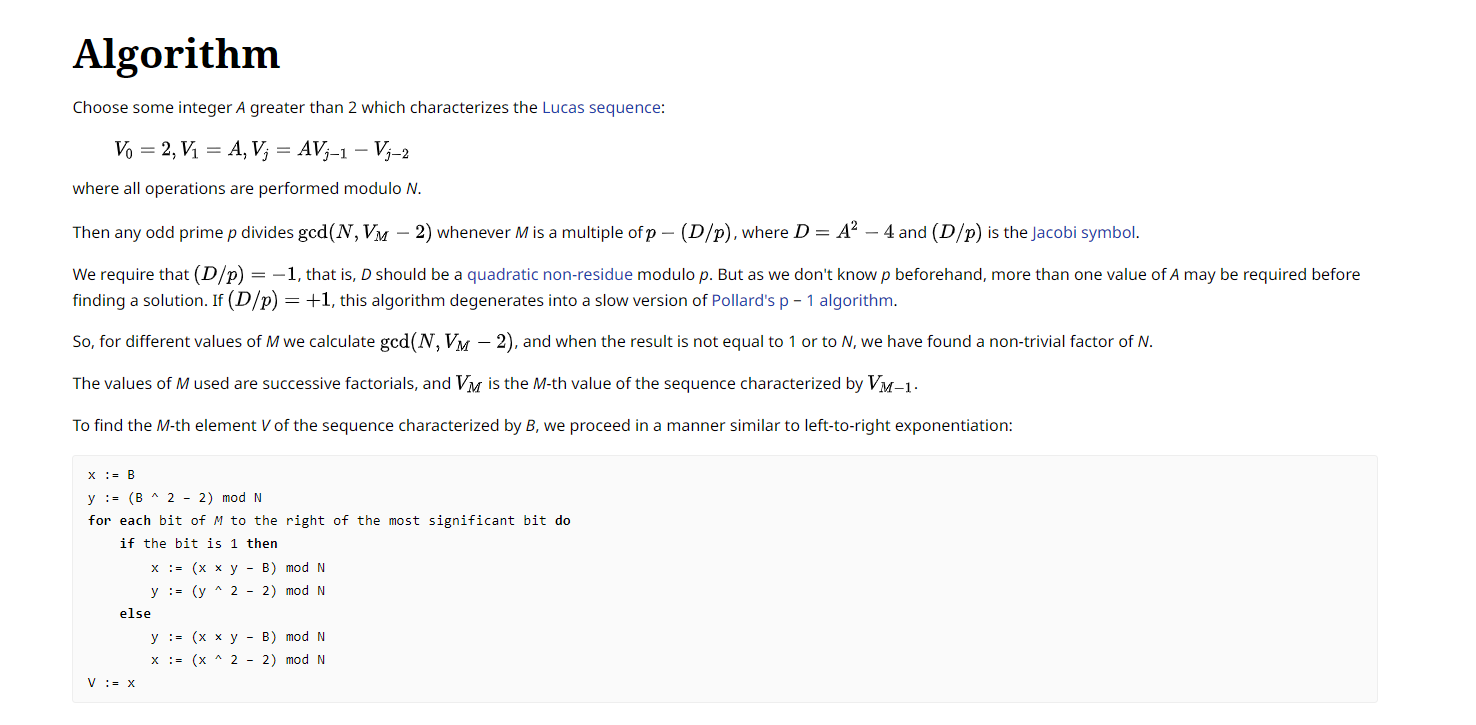
算法可以调用primefac里的williams_pp1。

Fermat

基于平方和与平方差公式，假设\(\small n=p\cdot q,p>q\)，令\(\small x=(p+q)/2,y=(p-q)/2\)，那么\(\small x^2-y^2=(p^2+2pq+q^2)/4-(p^2-2pq+q^2)/4=p\cdot q=n\)，那么我们可以枚举x，当\(\small x^2-n\)为平方数的时候，就能得到x和y的值，p和q也能通过加减消元求出。显然我们必须要让\(\small x^2-n\)大于0才可能有解，所以应该从\(\small x=\sqrt n\)开始枚举。而y越小则枚举次数会越少，即p和q越接近，则越容易分解，所以费马分解一般适用于p和q相差不大的时候。
为方便使用，可以自己实现一个集成到primefac里。

Pollard_rho

基于生日悖论和Floyd判环算法的概率性分解算法，具体原理见知乎，这个算法平常用的不太多，这里给一个简洁的实现。实际上primefac里也有的，叫做pollardrho_brent。

from fractions import gcd
import random

def pollards_rho(n):
    x = random.randint(2,n-2); y = x; d = 1; c=random.randint(1,n-1)
    f = lambda x: (x**2 + c) % n
    while d == 1:
        x = f(x); y = f(f(y))
        d = gcd(abs(x-y), n)
    if d != n: return d

n = 349810984018843*349810984018901
print(n)
start = __import__("time").time()
p = pollards_rho(n)
end = __import__("time").time()

print(p)
print(end - start)

Coppersmith

比较灵活，通常是已知某因子部分比特，利用LLL等算法将多项式环系数进行规约从而分解n。详情见copper相关论文即可。