SUSCTF 2022

Ez_Pager_Tiper

题目：

magic_box.py

class lfsr():
    def __init__(self, seed, mask, length):
        self.length_mask = 2 ** length - 1
        self.mask = mask & self.length_mask
        self.state = seed & self.length_mask

    def next(self):
        next_state = (self.state << 1) & self.length_mask
        i = self.state & self.mask & self.length_mask
        output = 0
        while i != 0:
            output ^= (i & 1)
            i = i >> 1
        next_state ^= output
        self.state = next_state
        return output

    def getrandbit(self, nbit):
        output = 0
        for _ in range(nbit):
            output = (output << 1) ^ self.next()
        return output


class generator():
    def __init__(self, lfsr1, lfsr2, magic):
        self.lfsr1 = lfsr1
        self.lfsr2 = lfsr2
        self.magic = magic

    def infinit_power(self, magic):
        return int(magic)

    def malicious_magic(self, magic):
        now = (-magic & magic)
        magic ^= now
        return int(now), int(magic)
    # 这是关键点
    def confusion(self, c1, c2):
        magic = self.magic
        output, cnt = magic, 0
        output ^= c1 ^ c2
        while magic:
            now, magic = self.malicious_magic(magic)
            cnt ^= now >> (now.bit_length() - 1)
            output ^= now
        output ^= cnt * c1
        return int(output)

    def getrandbit(self, nbit):
        output1 = self.lfsr1.getrandbit(nbit)
        output2 = self.lfsr2.getrandbit(nbit)
        return self.confusion(output1, output2)

problem.py

from Crypto.Util.number import *
from magic_box import *
from secret import mask1, mask2, seed1, seed2, seed3
n1, n2 = 64, 12

flag = 'SUSCTF{***}'

def encrypt(cipher, ipath, opath):
    ifile=open(ipath,'rb')
    ofile=open(opath,'wb')
    plaintext=ifile.read()
    for ch in plaintext:
        c=ch^cipher.getrandbit(8)
        ofile.write(long_to_bytes(c))
    ifile.close()
    ofile.close()

def problem1():
    r = getRandomInteger(6)
    magic = 1<<r
    lfsr1 = lfsr(seed1, mask1, n1)
    lfsr2 = lfsr(seed2, mask2, n2)
    cipher = generator(lfsr1, lfsr2, magic)
    encrypt(cipher, "MTk4NC0wNC0wMQ==_6d30.txt", "MTk4NC0wNC0wMQ==_6d30.enc")

def problem2():
    magic = getPrime(64)
    lfsr1=lfsr(seed1, mask1, n1)
    lfsr2=lfsr(seed3, mask2, n2)
    cipher = generator(lfsr1, lfsr2, magic)
    encrypt(cipher, "MTk4NC0xMi0yNQ==_76ff.txt", "MTk4NC0xMi0yNQ==_76ff.enc")
    # flag in it?
    print(f'hint={magic}')
    # hint = 15193544052573546419

problem1()
problem2()

分析：
1.magic_box是自己实现的基于lfsr的混淆算法，整个算法的重点在于confusion()函数，直接分析函数会发现有点复杂，所以采取直接测试的办法看看函数的输出：

def malicious_magic(magic):
    now = (-magic & magic)
    magic ^= now
    return int(now), int(magic)

def confusion(magic,c1, c2):
    output, cnt = magic, 0
    output ^= c1 ^ c2
    while magic:
        now, magic = malicious_magic(magic)
        cnt ^= now >> (now.bit_length() - 1)
        output ^= now
    output ^= cnt * c1
    return int(output)

print(4^5)
# 1
print(confusion(0b1001,4,5))
print(confusion(0b100111,4,5))
print(confusion(0b10100,4,5))
# 1
# 1
# 1
print(confusion(0b111,4,5))
print(confusion(0b111101,4,5))
print(confusion(0b111,5,4))
# 5
# 5
# 4

通过测试可以发现当magic二进制有奇数个1的时候，在problem中输出lfsr2，当有偶数个1的时候输出lfsr1^lfsr2；而problem1中的magic二进制是奇数个1，因此输出是lfsr2，可以考虑通过problem1来恢复mask2。
观察一下题目中给的data文件内容：

可以猜测第一行为Date 19xxxxx-x1，然后把文件名base64解密，发现也是这个格式，于是猜测第一行内容就是文件名的明文。
那么可以通过明文和密文异或得到lfsr2的输出，lfsr的序列生成过程本质上可以看作mod2加法，于是可以通过建立mod2下的矩阵方程求解mask2：

\[\Large\left[ \begin{matrix} a_{0} & a_{1} & \cdots & a_{11} \\ a_{1} & a_{2} & \cdots & a_{12} \\ \vdots & \vdots & \ddots & \vdots \\ a_{11} & a_{12} & \cdots & a_{22} \\ \end{matrix} \right] * \left[ \begin{matrix} mask_{0}\\ mask_{1}\\ \vdots \\ mask_{11}\\ \end{matrix} \right] = \left[ \begin{matrix} a_{12}\\ a_{13}\\ \vdots \\ a_{23}\\ \end{matrix} \right] \]

from Crypto.Util.number import *
from Crypto.Util.strxor import *
 
plain1 = b'Date: 1984-04-01'
ciper1 = open('MTk4NC0wNC0wMQ==_6d30.enc', 'rb').read()
output1 = strxor(plain1, ciper1[:len(plain1)])
output1 = bytes_to_long(output1)
s = [int(x) for x in bin(output1)[2:]]
 
M = matrix(GF(2), 12, 12)
T = vector(GF(2), 12)
# 注意倒置a0到a11
for i in range(12):
        M[i] = s[i : i + 12]
        T[i] = s[i+12]
mask = M^(-1) * T
print(mask)
#(1, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 1)

当然这个矩阵求解过程也可以利用别人造的轮子：

def get_key(mask,key,degree):
    R = ""
    index = 0
    key = key[degree-1] + key[:degree]
    while index < degree:
        tmp = 0
        for i in range(degree):
            if mask >> i & 1:
                # tmp ^= int(key[255 - i])
                tmp = (tmp+int(key[degree-1-i]))%2
        R = str(tmp) + R
        index += 1
        key = key[degree-1] + str(tmp) + key[1:degree-1]
    return int(R,2)

def get_int(x,degree):
    m=''
    for i in range(degree):
        m += str(x[i])
    return (int(m,2))

def BM(r,degree):
    a=[]
    for i in range(len(r)):
        a.append(int(r[i]))       #将 r 转换成列表a = [0,0,1,...,]格式    
    res = []
    for i in range(degree):
        for j in range(degree):
            if a[i+j]==1:
                res.append(1)
            else:
                res.append(0)
    sn = []
    for i in range(degree):
        if a[degree+i]==1:
            sn.append(1)
        else:
            sn.append(0)
    MS = MatrixSpace(GF(2),degree,degree)        #构造 256 * 256 的矩阵空间
    MSS = MatrixSpace(GF(2),1,degree)         #构造 1 * 256 的矩阵空间
    A = MS(res)
    s = MSS(sn)                       #将 res 和 sn 的值导入矩阵空间中
    try:
        inv = A.inverse()            # 求A 的逆矩阵
    except ZeroDivisionError as e:
        return -1,-1
    mask = s*inv 
    return get_key(get_int(mask[0],degree),r[:degree],degree),get_int(mask[0],degree)

from Crypto.Util.number import *
from Crypto.Util.strxor import *

n1, n2 = 64, 12
plain1 = b'Date: 1984-04-01'
ciper1 = open('MTk4NC0wNC0wMQ==_6d30.enc', 'rb').read()
output1 = strxor(plain1, ciper1[:len(plain1)])
output1 = bytes_to_long(output1)
s = bin(output1)[2:]
print(BM(s,12))
# (2989, 2053) 前一个是seed，后一个是mask

2.通过已知信息攻击problem2。首先magic有偶数个1所以输出是LFSR1^LFSR2，因为LFSR2的seed3仅12bit，所以可进行爆破，并通过文件名提供的部分明文可恢复LFSR1的部分明文，然后再类似1的操作去求解mask1和seed1，最后通过SUSCTF过滤得到正确的flag。
exp：
这部分的exp参考了等风师傅的

from base64 import *
from Crypto.Util.number import *
n1=64
n2=12

class lfsr():
    def __init__(self, seed, mask, length):
        self.length_mask = 2 ** length - 1
        self.mask = mask & self.length_mask
        self.state = seed & self.length_mask

    def next(self):
        next_state = (self.state << 1) & self.length_mask
        i = self.state & self.mask & self.length_mask
        output = 0
        while i != 0:
            output ^^= (i & 1)
            i = i >> 1
        next_state ^^= output
        self.state = next_state
        return output

    def getrandbit(self, nbit):
        output = 0
        for _ in range(nbit):
            output = (output << 1) ^^ self.next()
        return output

def get_key(mask,key,degree):
    R = ""
    index = 0
    key = key[degree-1] + key[:degree]
    while index < degree:
        tmp = 0
        for i in range(degree):
            if mask >> i & 1:
                # tmp ^= int(key[255 - i])
                tmp = (tmp+int(key[degree-1-i]))%2
        R = str(tmp) + R
        index += 1
        key = key[degree-1] + str(tmp) + key[1:degree-1]
    return int(R,2)

def get_int(x,degree):
    m=''
    for i in range(degree):
        m += str(x[i])
    return (int(m,2))

def BM(r,degree):
    a=[]
    for i in range(len(r)):
        a.append(int(r[i]))       #将 r 转换成列表a = [0,0,1,...,]格式    
    res = []
    for i in range(degree):
        for j in range(degree):
            if a[i+j]==1:
                res.append(1)
            else:
                res.append(0)
    sn = []
    for i in range(degree):
        if a[degree+i]==1:
            sn.append(1)
        else:
            sn.append(0)
    MS = MatrixSpace(GF(2),degree,degree)        #构造 256 * 256 的矩阵空间
    MSS = MatrixSpace(GF(2),1,degree)         #构造 1 * 256 的矩阵空间
    A = MS(res)
    s = MSS(sn)                       #将 res 和 sn 的值导入矩阵空间中
    try:
        inv = A.inverse()            # 求A 的逆矩阵
    except ZeroDivisionError as e:
        return -1,-1
    mask = s*inv 
    return get_key(get_int(mask[0],degree),r[:degree],degree),get_int(mask[0],degree)

Name=b'Date: 1984-12-25'
with open ('MTk4NC0xMi0yNQ==_76ff.enc','rb') as f:
    Data=f.read()
bits=''
# 已知的明文异或密文得到LFSR1^LFSR2
for i in range(len(Name)):
    tmp=bin(Data[:len(Name)][i]^^Name[i])[2:].zfill(8)
    bits+=tmp
# 爆破seed3并用BM算法求解
for seed3 in range(1<<n2,0,-1):
    lfsr2=lfsr(seed3,mask2,n2)
    output2=''
    for j in range(len(Name)):
        tmp=lfsr2.getrandbit(8)
        output2+=bin(tmp)[2:].zfill(8)
    output1=int(bits,2)^^int(output2,2)
# BM攻击需要64*2长度的连续输出位
    output1=bin(output1)[2:].zfill(128)
    seed1,mask1=BM(output1,64)
# 发生求逆失败时
    if seed1==-1 and mask1==-1:
        continue
    lfsr1=lfsr(seed1,mask1,n1)
    lfsr2=lfsr(seed3,mask2,n2)
    flag=b''
    for i in Data:
        temp=i^^lfsr1.getrandbit(8)^^lfsr2.getrandbit(8)
        flag+=long_to_bytes(temp)
    print(seed3)
    if b'SUSCTF' in flag:
        print(flag)
#b"Date: 1984-12-25\r\nThough the hunger pangs were no longer so exquisite, he realized that he was weak.  He was compelled to pause for frequent rests, when he attacked the muskeg berries and rush-grass patches.  His tongue felt dry and large, as though covered with a fine hairy growth, and it tasted bitter in his mouth.  His heart gave him a great deal of trouble.  When he had travelled a few minutes it would begin a remorseless thump, thump, thump, and then leap up and away in a painful flutter of beats that choked him and made him go faint and dizzy.\r\nIn the middle of the day he found two minnows in a large pool.  It was impossible to bale it, but he was calmer now and managed to catch them in his tin bucket.  They were no longer than his little finger, but he was not particularly hungry.  The dull ache in his stomach had been growing duller and fainter.  It seemed almost that his stomach was dozing.  He ate the fish raw, masticating with painstaking care, for the eating was an act of pure reason.  While he had no desire to eat, he knew that he must eat to live.\r\nIn the evening he caught three more minnows, eating two and saving the third for breakfast.  The sun had dried stray shreds of moss, and he was able to warm himself with hot water.  He had not covered more than ten miles that day; and the next day, travelling whenever his heart permitted him, he covered no more than five miles.  But his stomach did not give him the slightest uneasiness.  It had gone to sleep.  He was in a strange country, too, and the caribou were growing more plentiful, also the wolves.  Often their yelps drifted across the desolation, and once he saw three of them slinking away before his path.\r\nThe content is an excerpt from Love of Life, by Jack London. The problem is mainly about LFSR and I've tried not to make it hard (with the cost of some running time, actually). Your flag is SUSCTF{Thx_f0r_y0uR_P4ti3nce_:)_GoodLuck!_1bc9b80142c24fef610b8d770b500009} and I hope you will enjoy our game. You'll find this problem so ez while solving other problems, which is created by --."

InverseProblem

题目：

problem.py

import numpy as np
from secret import flag

# 注意A是对称矩阵
def gravity(n,d=0.25):
    A=np.zeros([n,n])
    for i in range(n):
        for j in range(n):
            A[i,j]=d/n*(d**2+((i-j)/n)**2)**(-1.5)
    return A

n=len(flag)
A=gravity(n)
x=np.array(list(flag))
b=A@x
np.savetxt('b.txt',b)

分析：
1.本质上确实是个反问题，但是重点在于python浮点数的误差而非反问题。首先我们来测试一下python的浮点数：

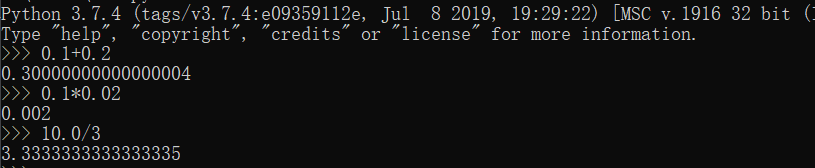
存在比较明显的误差，那么问题可以转化为已知\(A\cdot x=b+e\)求x，e为误差；这个问题显然是一个LWE，解决的方案比较多。
2.首先想到的是构造嵌入类型的格，即Embedded Technique，转成svp求解，构造方式以下两种都可以：

\[ \Large\left[ \begin{matrix} A & 0 \\ B & k \\ \end{matrix} \right] \]

或

\[ \Large\left[ \begin{matrix} A & k \\ B & 0 \\ \end{matrix} \right] \]

其中k为一个不过于大的非0数。
由于本题处理的是浮点数，为了方便操作可以考虑将数据全部扩大若干倍，变为整数矩阵运算。对于exp1，\(flag\cdot M=M.LLL()[0]\)，所以对解关于M的矩阵方程即可。对于exp2，是利用浮点数计算的，先计算出误差e，再解\(A\cdot flag = b-e\)。此外，本题实际上可以看作一个最近向量问题，所以又可以用babai进行计算，见exp3。
exp：

# exp1
import numpy as np
f=open('b.txt','r')
b=[]
for i in range(85):
    tmp=int(float(f.readline())*10^18)
    b.append(tmp)

def gravity(n,d=0.25):
    A=np.zeros([n,n])
    for i in range(n):
        for j in range(n):
            A[i,j]=d/n*(d**2+((i-j)/n)**2)**(-1.5)
    return A

# A是对称矩阵
A = gravity(85)
A = [[int(j*10^18) for j in i] for i in A]
 
M = []
for i in range(85):
    M.append(A[i] + [0])
 
M.append(b + [1000])
M = Matrix(ZZ, M)
ans = M.LLL()[0]
print(ans)
flag=list(M.solve_left(ans))
flag=list(map(abs,flag))
print(flag)
print(bytes(flag[:-1]))

# exp2
import numpy as np

def gravity(n,d=0.25):
    A=np.zeros([n,n])
    for i in range(n):
        for j in range(n):
            A[i,j]=d/n*(d**2+((i-j)/n)**2)**(-1.5)
    return A

b=np.loadtxt('b.txt')
n=len(b)
b=vector(QQ,b)
A=matrix(QQ,gravity(n).tolist())
M=block_matrix(QQ,[[A,zero_matrix(n,1)],[matrix(b),matrix([1e-12])]])
L=M.LLL()
x=A\(b-L[0][:-1])
flag=bytes(x).decode()
print(flag)

# exp3
from sage.modules.free_module_integer import IntegerLattice
import numpy as np

def gravity(n,d=0.25):
    A=np.zeros([n,n])
    for i in range(n):
        for j in range(n):
            A[i,j]=d/n*(d**2+((i-j)/n)**2)**(-1.5)
    return A

f=open('b.txt','r')
b=[]
for i in range(85):
    tmp=int(float(f.readline())*10^18)
    b.append(tmp)

A = gravity(85)
A = [[int(j*10^18) for j in i] for i in A]

b_V=vector(ZZ,b)
A=matrix(ZZ,A)

# Babai's Nearest Plane algorithm
def Babai_closest_vector(M, G, target):
    small = target
    for _ in range(5):
        for i in reversed(range(M.nrows())):
            c = ((small * G[i]) / (G[i] * G[i])).round()
            small -=  M[i] * c
    return target - small

lattice = IntegerLattice(A, lll_reduce=True)
print("LLL done")
# 约减基 lattice.reduced_basis
# 正交基 lattice.reduced_basis.gram_schmidt()[0]
gram = lattice.reduced_basis.gram_schmidt()[0]
target = vector(ZZ, b_V)
re = Babai_closest_vector(lattice.reduced_basis, gram, target)
print("Closest Vector: {}".format(re))
# 去掉误差后，解矩阵方程
ingredients = A.solve_left(re)
print("Ingredients: {}".format(ingredients))

m = ''
for i in range(len(ingredients)):
    m += chr(ingredients[i])
print(m)
# SUSCTF{Maybe_th3_1nverse_Pr0b1em_has_s0m3thing_1n_comm0n_w1th_th3_LWE_Search_Problem}

SpecialCurve3

参考paper，e1的求解是paper中不安全的参数，e2的求解是a=0的特殊情况，两种情况分别做乘法群映射和加法群映射进行攻击；e3参数安全，但群阶p+1光滑，那么利用Pohlig-Hellman攻击即可，官方wp的做法是做了映射再Pohlig-Hellman求解，实际上映射前后安全性一致，不做映射也行。

p1,a1,b1 = (233083587295210134948821000868826832947,73126617271517175643081276880688551524,88798574825442191055315385745016140538)
p2,a2,b2 = (191068609532021291665270648892101370598912795286064024735411416824693692132923,0,58972296113624136043935650439499285317465012097982529049067402580914449774185)
p3,a3,b3 = (52373730653143623993722188411805072409768054271090317191163373082830382186155222057388907031638565243831629283127812681929449631957644692314271061305360051,28655236915186704327844312279364325861102737672471191366040478446302230316126579253163690638394777612892597409996413924040027276002261574013341150279408716,42416029226399083779760024372262489355327595236815424404537477696856946194575702884812426801334149232783155054432357826688204061261064100317825443760789993)

print(kronecker(a1,p1))
print(kronecker(a2,p2)) # a = 0的特殊情况
print(kronecker(a3,p3))

from Crypto.Util.number import *

class SpecialCurve:
    def __init__(self,p,a,b):
        self.p=p
        self.a=a
        self.b=b

    def __str__(self):
        return f'SpecialCurve({self.p},{self.a},{self.b})'

    def add(self,P1,P2):
        x1,y1=P1
        x2,y2=P2
        if x1==0:
            return P2
        elif x2==0:
            return P1
        elif x1==x2 and (y1+y2)%self.p==0:
            return (0,0)
        if P1==P2:
            t=(2*self.a*x1-self.b)*inverse(2*y1,self.p)%self.p
        else:
            t=(y2-y1)*inverse(x2-x1,self.p)%self.p
        x3=self.b*inverse(self.a-t**2,self.p)%self.p
        y3=x3*t%self.p
        return (x3,y3)

    def mul(self,P,k):
        assert k>=0
        Q=(0,0)
        while k>0:
            if k%2:
                k-=1
                Q=self.add(P,Q)
            else:
                k//=2
                P=self.add(P,P)
        return Q

curve1=SpecialCurve(233083587295210134948821000868826832947,73126617271517175643081276880688551524,88798574825442191055315385745016140538)
G1=(183831340067417420551177442269962013567, 99817328357051895244693615825466756115)
Q1=(166671516040968894138381957537903638362, 111895361471674668502480740000666908829)
p=curve1.p
a=curve1.a

# P.<k> = PolynomialRing(GF(p))  
# f = k^2 - a 
# f.roots()

# theta = 127498493720245280357325638454055005176
# kg=GF(p)(G1[1])/GF(p)(G1[0])
# kq=GF(p)(Q1[1])/GF(p)(Q1[0])184572164865068633286768057743716588370
# tq=(kq+theta)/(kq-theta)
# print('Starting discrete log...')
# e1=tq.log(tg)
# print(e1)
e1 = 184572164865068633286768057743716588370

curve2=SpecialCurve(191068609532021291665270648892101370598912795286064024735411416824693692132923,0,58972296113624136043935650439499285317465012097982529049067402580914449774185)
G2=(91006613905368145804676933482275735904909223655198185414549961004950981863863, 96989919722797171541882834089135074413922451043302800296198062675754293402989)
Q2=(13504049588679281286169164714588439287464466303764421302084687307396426249546, 110661224324697604640962229701359894201176516005657224773855350780007949687952)

p=curve2.p
kg=GF(p)(G2[0])/GF(p)(G2[1])
kq=GF(p)(Q2[0])/GF(p)(Q2[1])
e2=kq/kg
print(e2)

curve3=SpecialCurve(52373730653143623993722188411805072409768054271090317191163373082830382186155222057388907031638565243831629283127812681929449631957644692314271061305360051,28655236915186704327844312279364325861102737672471191366040478446302230316126579253163690638394777612892597409996413924040027276002261574013341150279408716,42416029226399083779760024372262489355327595236815424404537477696856946194575702884812426801334149232783155054432357826688204061261064100317825443760789993)
G3=(15928930551986151950313548861530582114536854007449249930339281771205424453985946290830967245733880747219865184207937142979512907006835750179101295088805979, 29726385672383966862722624018664799344530038744596171136235079529609085682764414035677068447708040589338778102975312549905710028842378574272316925268724240)
Q3=(38121552296651560305666865284721153617113944344833289618523344614838728589487183141203437711082603199613749216407692351802119887009907921660398772094998382, 26933444836972639216676645467487306576059428042654421228626400416790420281717654664520663525738892984862698457685902674487454159311739553538883303065780163)

# 验证阶为p+1
Q=curve3.mul(G3,curve3.p+1)
print(Q)

import requests

def queryFactors(n):
    s=[]
    url="http://factordb.com/api?query="+str(n)
    r = requests.get(url)
    factors=r.json()['factors']
    for f in factors:
        for i in range(f[1]):
            s.append(int(f[0]))
    return s

Factors = queryFactors(curve3.p+1)
# dlogs=[]
# for i in Factors:
#     Now=(0,0)
#     tmpG=curve3.mul(G3,ZZ((curve3.p+1))//ZZ(i))
#     tmpQ=curve3.mul(Q3,ZZ((curve3.p+1))//ZZ(i))
#     for dlog in range(i):
#         Now=curve3.add(Now,tmpG)
#         if Now==tmpQ:
#             dlogs.append(int(dlog))
#             break
# print(dlogs)
dlogs = [1, 1, 1278, 3225, 11716, 15045, 11942, 8667, 9594, 13097, 4598, 8039, 33435, 23446, 12971, 13296, 55727, 9502, 11344, 68793, 72552, 4926, 29058, 69368, 4520, 37272, 45247, 47190, 18836, 60541, 36333, 27743, 33, 12206, 62705]
e3 = crt(dlogs,Factors)+1
print(e3)

import hashlib
enc=4161358072766336252252471282975567407131586510079023869994510082082055094259455767245295677764252219353961906640516887754903722158044643700643524839069337
flag=enc^^bytes_to_long(hashlib.sha512(b'%d-%d-%d'%(e1,e2,e3)).digest())
print(long_to_bytes(flag))
# SUSCTF{Y0u_kNow_c0n1c_curv3_anD_discrete_l0g_vEry_we11~}

large case

from Crypto.Util.number import *
from gmpy2 import *
from primefac import primefac

L = 128
def get_e(p):
    for i in primefac(p-1):
        if pow(c % p, (p - 1) // i, p) == 1 and i != 2:
            print(i)
            break

c = 2832775557487418816663494645849097066925967799754895979829784499040437385450603537732862576495758207240632734290947928291961063611897822688909447511260639429367768479378599532712621774918733304857247099714044615691877995534173849302353620399896455615474093581673774297730056975663792651743809514320379189748228186812362112753688073161375690508818356712739795492736743994105438575736577194329751372142329306630950863097761601196849158280502041616545429586870751042908365507050717385205371671658706357669408813112610215766159761927196639404951251535622349916877296956767883165696947955379829079278948514755758174884809479690995427980775293393456403529481055942899970158049070109142310832516606657100119207595631431023336544432679282722485978175459551109374822024850128128796213791820270973849303929674648894135672365776376696816104314090776423931007123128977218361110636927878232444348690591774581974226318856099862175526133892
p = 127846753573603084140032502367311687577517286192893830888210505400863747960458410091624928485398237221748639465569360357083610343901195273740653100259873512668015324620239720302434418836556626441491996755736644886234427063508445212117628827393696641594389475794455769831224080974098671804484986257952189021223
q = 145855456487495382044171198958191111759614682359121667762539436558951453420409098978730659224765186993202647878416602503196995715156477020462357271957894750950465766809623184979464111968346235929375202282811814079958258215558862385475337911665725569669510022344713444067774094112542265293776098223712339100693
r = 165967627827619421909025667485886197280531070386062799707570138462960892786375448755168117226002965841166040777799690060003514218907279202146293715568618421507166624010447447835500614000601643150187327886055136468260391127675012777934049855029499330117864969171026445847229725440665179150874362143944727374907
get_e(p)
get_e(q)
get_e(r)
n = p*q*r
e = 757 * 66553 * 5156273

# 消除L位的十六进制的padding(在删除r之前)
c = c * invert(pow(2,8 * L * e,n),n) % n

# 缩小e:删除r以及更改各个指标的受r的影响
e = e // 5156273
phi_n_without_r = (p - 1) * (q - 1)
n = n // r
d1 = invert(5156273,phi_n_without_r)
c = pow(c,d1,n)

# 在删除r后消除padding
# c = c * gmpy2.invert(pow(2,8 * L * now_e,n),n) % n

# 算法一
phi = phi_n_without_r // e
g = 1
g_E = pow(g,phi,n)
# g_E不是1即可
while g_E == 1:
    g = g + 1
    g_E = pow(g,phi,n)
print(g,g_E)

# 算法二
d = invert(e,phi)
tmp = pow(c,d,n)

for _ in range(e):
    flag = tmp
    if b"SUSCTF" in long_to_bytes(flag):
        print()
        print(long_to_bytes(flag))
        break
    else:
        tmp = tmp * g_E % n