CryptoCTF 2022 (part2)

medium

Aniely

题目：

点击查看代码

#!/usr/bin/env python3

from struct import *
from os import *
from secret import passphrase, flag

def aniely_stream(passphrase):
	def mixer(u, v):
		return ((u << v) & 0xffffffff) | u >> (32 - v) # 循环移位v位

	def forge(w, a, b, c, d):
		for i in range(2):
			w[a] = (w[a] + w[b]) & 0xffffffff
			w[d] = mixer(w[a] ^ w[d], 16 // (i + 1))
			w[c] = (w[c] + w[d]) & 0xffffffff
			w[b] = mixer(w[b] ^ w[c], (12 + 2*i) // (i + 1))

	bring = [0] * 16
	bring[:4] = [0x61707865, 0x3320646e, 0x79622d32, 0x6b206574]
	bring[4:12] = unpack('<8L', passphrase)
	bring[12] = bring[13] = 0x0
	bring[14:] = [0] * 2

	while True:
		w = list(bring)
		for _ in range(10):
			forge(w, 0x0, 0x4, 0x8, 0xc)
			forge(w, 0x1, 0x5, 0x9, 0xd)
			forge(w, 0x2, 0x6, 0xa, 0xe)
			forge(w, 0x3, 0x7, 0xb, 0xf)
			forge(w, 0x0, 0x5, 0xa, 0xf)
			forge(w, 0x1, 0x6, 0xb, 0xc)
			forge(w, 0x2, 0x7, 0x8, 0xd)
			forge(w, 0x3, 0x4, 0x9, 0xe)
		for c in pack('<16L', *((w[_] + bring[_]) & 0xffffffff for _ in range(16))):
			yield c
		bring[12] = (bring[12] + 1) & 0xffffffff
		if bring[12] == 0:
			bring[13] = (bring[13] + 1) & 0xffffffff

def aniely_encrypt(msg, passphrase):
	if len(passphrase) < 32:
		passphrase = (passphrase * (32 // len(passphrase) + 1))[:32]
	rand = urandom(2) * 16
	return bytes(a ^ b ^ c for a, b, c in zip(msg, aniely_stream(passphrase), rand))

key = bytes(a ^ b for a, b in zip(passphrase, flag))
enc = aniely_encrypt(passphrase, key)
print(f'key = {key.hex()}')
print(f'enc = {enc.hex()}')

分析：
经测试aniely_stream()是生成序列的迭代器，并且它用的key已经给了，因此可以通过求这个序列加上爆破2个字节的random得到passphrase，得到passphrase以后再和key异或得到flag，可通过flag的头部格式来判断是否正确。
exp：

from struct import *
import itertools

def aniely_stream(passphrase):
    def mixer(u, v):
        return ((u << v) & 0xffffffff) | u >> (32 - v)  # 循环移位v位

    def forge(w, a, b, c, d):
        for i in range(2):
            w[a] = (w[a] + w[b]) & 0xffffffff
            w[d] = mixer(w[a] ^ w[d], 16 // (i + 1))
            w[c] = (w[c] + w[d]) & 0xffffffff
            w[b] = mixer(w[b] ^ w[c], (12 + 2 * i) // (i + 1))

    bring = [0] * 16
    bring[:4] = [0x61707865, 0x3320646e, 0x79622d32, 0x6b206574]
    bring[4:12] = unpack('<8L', passphrase)
    bring[12] = bring[13] = 0x0
    bring[14:] = [0] * 2

    while True:
        w = list(bring)
        for _ in range(10):
            forge(w, 0x0, 0x4, 0x8, 0xc)
            forge(w, 0x1, 0x5, 0x9, 0xd)
            forge(w, 0x2, 0x6, 0xa, 0xe)
            forge(w, 0x3, 0x7, 0xb, 0xf)
            forge(w, 0x0, 0x5, 0xa, 0xf)
            forge(w, 0x1, 0x6, 0xb, 0xc)
            forge(w, 0x2, 0x7, 0x8, 0xd)
            forge(w, 0x3, 0x4, 0x9, 0xe)
        for c in pack('<16L', *((w[_] + bring[_]) & 0xffffffff for _ in range(16))):
            yield c
        bring[12] = (bring[12] + 1) & 0xffffffff
        if bring[12] == 0:
            bring[13] = (bring[13] + 1) & 0xffffffff


key = '4dcceb8802ae3c45fe80ccb364c8de19f2d39aa8ebbfb0621623e67aba8ed5bc'
enc = 'e67a67efee3a80b66af0c33260f96b38e4142cd5d9426f6f156839f2e2a8efe8'

key, enc = map(bytes.fromhex, (key, enc))
print(len(key))

if __name__ == '__main__':

    for rand in itertools.product(range(256), repeat=2):
        #print(rand)
        k = aniely_stream(key)
        rand = bytes(rand) * 16
        passphrase = bytes(a ^ b ^ c for a, b, c in zip(enc, k, rand))
        msg = bytes(a ^ b for a, b in zip(passphrase, key))
        if (msg.startswith(b'CCTF{')):
            print(msg)
            break
        #b'CCTF{7rY_t0_D3cRyPT_z3_ChaCha20}'

Diploma

题目：
求矩阵群的阶，应该有若干轮：

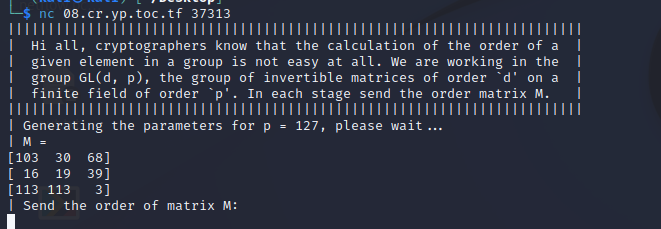
分析：
1.sagemath矩阵群求阶：

p = 127
G = GL(3, GF(p))
M = [
[  5, 125, 116],
[ 73,  69,  44],
[ 39,  68,  64]
]
M = G(M)
print(M.order())

2.sagemath的乘法群求阶：

M = [
[  5, 125, 116],
[ 73,  69,  44],
[ 39,  68,  64]]
M = Matrix(GF(q), M)
M.multiplicative_order()

exp：
因为要读取矩阵所以比较难写：

# sagemath
from pwn import *

io = remote('213.233.181.98',37313)
io.recvlines(8)
d = 3

def Go(m,d):
    p = 127
    G = GL(d, GF(p))
    M = m
    M = G(M)
    order = M.order()
    print(order)
    io.sendline(bytes(str(order),encoding='utf-8'))

while True:
    print('Start...')
    print('Now d is:',d)
    l = []
    for i in range(d):
        l1 = []
        tmp = io.recvline()
        print(tmp)
        for j in range(1,2+d-1+3*d,4):
            l1.append(int(tmp[j:j+3]))
        l.append(l1)
    print(l)
    io.recvline()
    Go(l,d)
    d = d+1
    if d == 15:
        print(io.recvline())
    print(io.recvlines(3))

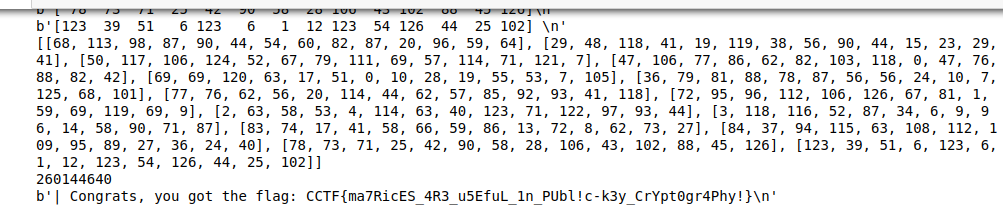
Cantilever

题目：

点击查看代码

#!/usr/bin/env python3

from Crypto.Util.number import *
from flag import flag

def gen_primes(nbit, imbalance):
	p = 2
	FACTORS = [p]
	while p.bit_length() < nbit - 2 * imbalance:
		factor = getPrime(imbalance)
		FACTORS.append(factor)
		p *= factor
	rbit = (nbit - p.bit_length()) // 2

	while True:
		r, s = [getPrime(rbit) for _ in '01']
		_p = p * r * s
		if _p.bit_length() < nbit: rbit += 1
		if _p.bit_length() > nbit: rbit -= 1
		if isPrime(_p + 1):
			FACTORS.extend((r, s))
			p = _p + 1
			break

	FACTORS.sort()
	return (p, FACTORS)

def genkey(nbit, imbalance, e):
	while True:
		p, FACTORS = gen_primes(nbit // 2, imbalance)
		if len(FACTORS) != len(set(FACTORS)):
			continue
		q, q_factors = gen_primes(nbit // 2, imbalance + 1)
		if len(q_factors) != len(set(q_factors)):
			continue
		factors = FACTORS + q_factors
		if e not in factors:
			break
	n = p * q
	return n, (p, q)

nbit = 2048
imbalance = 19
e = 0x10001

m_1 = bytes_to_long(flag[:len(flag) // 2])
m_2 = bytes_to_long(flag[len(flag) // 2:])

n, PRIMES = genkey(nbit, imbalance, e)

c_1 = pow(m_1, e, n)
c_2 = pow(e, m_2, n)

print(f'n = {n}')
print(f'c_1 = {c_1}')
print(f'c_2 = {c_2}')

分析：
围绕着\(p-1\)光滑的两种攻击：对于大数分解问题的\(Pollard p-1\)算法，对于离散对数问题的 \(Pohlig-Hellman\)算法.
exp：

from Crypto.Util.number import *
from gmpy2 import *

def Pollards_p_1(N):
    a = 2
    n = 2
    while True:
        a = pow(a, n, N)
        res = gcd(a-1, N)
        if res != 1 and res != N:
            print ('n =', n)
            print ('p =', res)
            return res
        n += 1

if __name__ == '__main__':
    # 第一部分 p光滑可分解n 然后解rsa
    e = 0x10001
    N = 7069789930583271525053215046247773438899869283661158227309691853515987055334306019600324056376312479212090202373516405860759222837585952590589336295698718699890424169542280710721069784487366121478569760563045886361884895363592898476736269784284754788133722060718026577238640218755539268465317292713320841554802703379684173485217045274942603346947299152498798736808975912326592689302969859834957202716983626393365387411319175917999258829839695189774082810459527737342402920881184864625678296442001837072332161966439361793009893108796934406114288057583563496587655548536011677451960307597573257032154009427010069578913
    c1 = 488692928085934899944055554857568564903346089951134051486941368561567330884363274156339625953702601270565654444836193796061118053575538224794730472032345171432952984560662218697488844007827176184413713651118743456250147472678673801728916283759932987216388378211555067885210167894310696549664382751443669387953644382833924884208966436685137553434532738845959014828804809425096115758364136546390809453200055265653531950423111482644330073443545410319576097902472017235065047191133112557289289189187696092145850680765843608118584107829268136014912479701945735063525799796920293418182776436767911172221104640501952880057
    # Pollards_p_1(N)
    p = 83408372012221120677052349409462320990177094246143674474872152829440524098582262384066400107950985845255268335597502228206679771838750219696329523257176739436871327238322817403970284015587320158034304282786944710043150568360761457471641695390427267786485448748458445872307883254297662715749746270343116946519
    q = N//p
    phi = (p-1)*(q-1)
    d = invert(e,phi)
    print(long_to_bytes(pow(c1,d,N)))

    # 第二部分 ph算法加crt求解

    n = 7069789930583271525053215046247773438899869283661158227309691853515987055334306019600324056376312479212090202373516405860759222837585952590589336295698718699890424169542280710721069784487366121478569760563045886361884895363592898476736269784284754788133722060718026577238640218755539268465317292713320841554802703379684173485217045274942603346947299152498798736808975912326592689302969859834957202716983626393365387411319175917999258829839695189774082810459527737342402920881184864625678296442001837072332161966439361793009893108796934406114288057583563496587655548536011677451960307597573257032154009427010069578913
    p = 83408372012221120677052349409462320990177094246143674474872152829440524098582262384066400107950985845255268335597502228206679771838750219696329523257176739436871327238322817403970284015587320158034304282786944710043150568360761457471641695390427267786485448748458445872307883254297662715749746270343116946519
    q = n // p
    c = 109770827223661560471527567179288748906402603483328748683689436879660543465776899146036833470531024202351087008847594392666852763100570391337823820240726499421306887565697452868723849092658743267256316770223643723095601213088336064635680075206929620159782416078143076506249031972043819429093074684182845530529249907297736582589125917235222921623698038868900282049587768700860009877737045693722732170123306528145661683416808514556360429554775212088169626620488741903267154641722293484797745665402402381445609873333905772582972140944493849645600529147490903067975300304532955461710562911203871840101407995813072692212

    G1 = GF(p)
    G2 = GF(q)
    c1 = G1(c)
    c2 = G2(c)
    g1 = G1(0x10001)
    g2 = G2(0x10001)
    k1 = discrete_log(c1, g1)
    k2 = discrete_log(c2, g2)
    m = crt([k1, k2], [p - 1, q - 1])
    print(m)
    print(long_to_bytes(m))
    # CCTF{5L3Ek_4s__s1lK__Ri9H7?!}

Oak land

题目：

点击查看代码

from Crypto.Util.number import *
from flag import flag

p = 7389313481223384214994762619823300589978423075857540712007981373887018860174846208000957230283669342186460652521580595183523706412588695116906905718440770776239313669678685198683933547601793742596023475603667
e = 31337
f = 7236042467316654159796543399639966340258093274047941788600980451877044636122969830708918356119442228154447395855689559447196348683125675305629837437591088260218138895919514078948650757100432223219969122629790
g = 1878626136321051642174045874618248475160620873585704351202865003185878331837410979441756843820270907300810543618813757245154196050399357659526631164136221434463496532263979506870318259276669412698827040743576

x = bytes_to_long(flag.encode('utf-8'))
assert x < p
c = (110 * pow(e, x, p) + 313 * pow(f, x, p) + 114 * pow(g, x, p)) % p
print(f'c = {c}')

分析：
\(c\)由\(e\),\(f\),\(g\)在\(mod(p)\)下的幂相加，猜测\(e与f与g\)之间存在线性关系可互相表示，于是把\(e^x\)求出之后再求解离散对数(\(p-1\)光滑)。
exp：

p = 7389313481223384214994762619823300589978423075857540712007981373887018860174846208000957230283669342186460652521580595183523706412588695116906905718440770776239313669678685198683933547601793742596023475603667
e = 31337
f = 7236042467316654159796543399639966340258093274047941788600980451877044636122969830708918356119442228154447395855689559447196348683125675305629837437591088260218138895919514078948650757100432223219969122629790
g = 1878626136321051642174045874618248475160620873585704351202865003185878331837410979441756843820270907300810543618813757245154196050399357659526631164136221434463496532263979506870318259276669412698827040743576
c = 871346503375040565701864845493751233877009611275883500035764036792906970084258238763963152627486758242101207127598485219754255161617890137664012548226251138485059295263306930653899766537171223837761341914356
F = GF(p)
# P.<t> = PolynomialRing(GF(p))
# f = 110*t + 313*t^(-1) + 114*t^(-2) - c
# ex = f.numerator().roots()[0][0]
R.<x> = Zmod(p)[]
f =110*x + 313*x^(-1) + 114*x^(-2) - c
f.roots()
e = F(e)
m = discrete_log(ex,e)
print(bytes.fromhex(hex(m)[2:]))
# b'CCTF{V33333rY_eeeeZy_DLP_cH41L3n9E!}'

Starter ECC

题目：

点击查看代码

#!/usr/bin/env sage
from Crypto.Util.number import *
from secret import n, a, b, x, flag

y = bytes_to_long(flag.encode('utf-8'))

assert y < n
E = EllipticCurve(Zmod(n), [a, b])

try:
	G = E(x, y)
	print(f'x = {x}')
	print(f'a = {a}')
	print(f'b = {b}')
	print(f'n = {n}')
	print('Find the flag :P')
except:
	print('Ooops, ERROR :-(')

分析：
\(ecc\)，已经给了\(a\)，\(b\)，\(n\)和横坐标\(x\)；但\(n\)可以分解为质数的乘积，所以不能直接用sagemath直接带入\(x\)求解，需要分解\(n\)，再把椭圆曲线放在这几个有限域上求解出来用中国剩余定理组合。
exp：

from Crypto.Util.number import *

# 椭圆曲线定义于有限域
a = 31337
b = 66826418568487077181425396984743905464189470072466833884636947306507380342362386488703702812673327367379386970252278963682939080502468506452884260534949120967338532068983307061363686987539408216644249718950365322078643067666802845720939111758309026343239779555536517718292754561631504560989926785152983649035
x = 10715086071862673209484250490600018105614048117055336074437503883703510511249361224931983788156958581275946729175531468251871452856923140435984577574698574803934567774824230985421074605062371141877954182153046477020617917601884853827611232355455223966039590143622792803800879186033924150173912925208583
q1 = 2^63
q2 = 690712633549859897233 ^ 6
q3 = 651132262883189171676209466993073 ^ 5
G1s = Mod(x ** 3 + a * x + b, q1).nth_root(2, all=True)
G2s = Mod(x ** 3 + a * x + b, q2).nth_root(2, all=True)
G3s = Mod(x ** 3 + a * x + b, q3).nth_root(2, all=True)

for G1 in G1s:
    for G2 in G2s:
        for G3 in G3s:
            m = long_to_bytes(int(crt([ZZ(G1), ZZ(G2), ZZ(G3)], [q1, q2, q3])))
            if b'CCTF{' in m:
                print(m)
                break
# CCTF{8E4uTy_0f_L1f7iN9_cOm3_Up!!}