Attacks on RSA by Lattice

Attacks on RSA by Lattice

Coppersmith

简介：coppersmith攻击简单来说就是通过格基规约在多项式时间内找到满足\(F(x)\equiv 0 (mod M)\)的小根，具体地，如果\(F(x)\)阶为\(d\)，那么小根\(x_0\)需要满足\(|x_0| < M^{1/d−\varepsilon}\)，\(\varepsilon\)是比0大的很小的值。
基本思想：找一个系数较小的多项式\(G(x)\)，使得\(G(x)\)由\(F(x)\)和\(M\)重构而成，从而利用求根公式或牛顿迭代法求出\(G(x)\)的根，也就是\(F(x)\equiv0(modM)\)的小根。这里给一个paper中的示例：

具体过程：
1.Howgrave-Graham定理
令\(M, X ∈ N\)，
\(F(x)=\sum_{i=0}^{d} a_{i}x^i\in Z[x]\)，
假设\(x_{0}\in Z\)是\(F(x)\equiv 0(modM)\)的根且\(|x_0|<X\)，
令行向量\(b_{F}=(a_0, a_1X, a_2X^2,...,a_dX^d).\)
在以上条件下，如果\(\|b_F\| < M/\sqrt{d+1}\)，则\(x_{0}\)是\(F(x)=0\)的根。
证明过程如下：

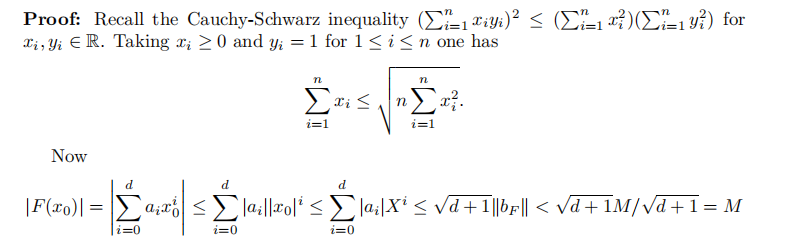
因为\(F(x)\equiv 0 (mod M)\)，所以\(F(x)=0\)。
2.格的构造思路
这一步实际上就是在上述条件下利用格基规约找到系数较小的多项式\(G(x)\)。
首先，paper的构造思路要求\(F(x)\)为首一多项式，当遇到\(F(x)\)最高次系数不为1的时候可以给整个式子乘上\(invert(a_d,M)\)，但这要求\(a_d\)和\(M\)互素。当\(a_d\)和\(M\)不互素的时候就要考虑把同余式拆成同余式组来处理。