机器学习里的信息论
一.信息量
信息论背后的原理是:从不太可能的事件中,能学到更多的信息,发生概率越小的事件信息量越大,独立事件包含额外的信息
信息量又译为信息本体,由克劳德·香农提出,用来衡量单一事件发生时所包含的信息量多寡。它的单位是bit,或是nats。
信息量是指一个事件所能够带来的信息的多少,这个事件发生的概率越小,其带来的信息量越大,也被称作自信息
自信息的含义包括两个方面:
1.自信息表示事件发生前,事件发生的不确定性。
2.自信息表示事件发生后,事件所包含的信息量,是提供给信宿的信息量,也是解除这种不确定性所需要的信息量

这仿佛和我们的直觉相反,假如有一个全知全能的上帝,他知道宇宙所有的信息,任何事件对他来说都是确定无疑的,任何事情发生的概率都是1,那他脑中的信息量一定是很大的
但是按照信息量的概念,他的信息量却为0,这是怎么回事呢,正如定义所描述的信息量是解除事件不确定性需要的信息,下图给出了一个直观的解释
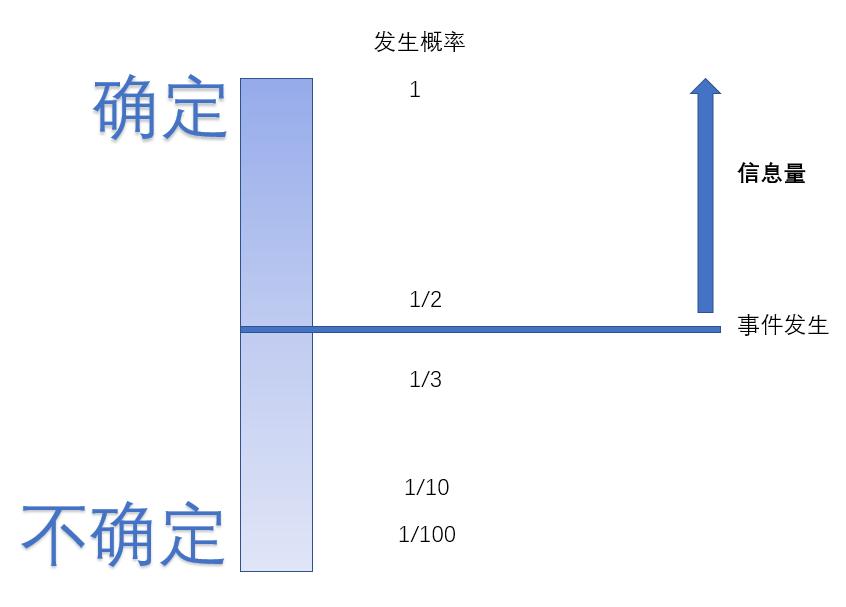
任何事件的发生概率都介于0到1之间,确定的一极是有边界的,这个边界是1
但是不确定的一极是没有边界的,只能无限小趋于0却不能等于0,因为0也是确定的,即这件事一定不会发生
我们总要选一个信息量为0的标杆,就像重力势能一样,信息也只有相互比较才有意义,信息学家们选择了概率为1作为这个标杆
所以信息量的概念:解除事件不确定性需要的信息(事件越不确定就意味着越混乱,我认为这个概念起名为信息熵才很恰当,但是信息熵另有其他含义)
那如何量化这个概念呢,再举一个例子(以下图源王木头学科学)
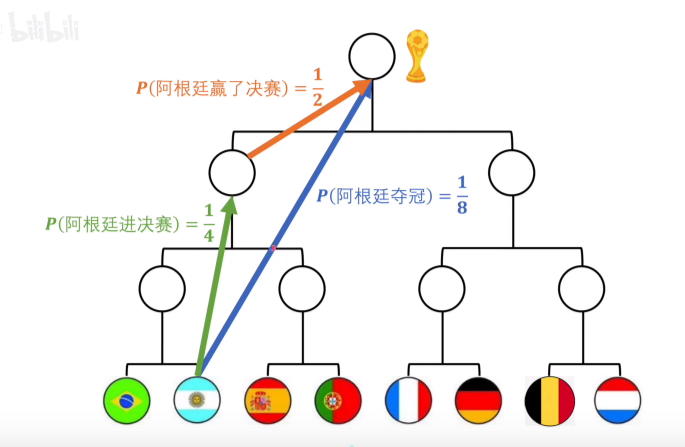
已知足球比赛中,阿根廷夺冠这件事 和 阿根廷进决赛并且赢了决赛,表达的是同一个意思,都是从夺冠概率1/8到夺冠这件事发生,那么这两件事的信息量应该是一致的,就有

所以 f 就被定义为(注意这里是人为规定的 一个符合上述两条规律的函数)
![]()
这里的底数取2的原因是,如果底数取2,这个量就有了物理含义,它代表确定这个事件所需的比特位数,比如一个事件有A,B,C,D四种情况,每种情况发生概率为1/4,这样f(1/4)=2,意思是2个bit可以确定这些情况,分别是00,01,10,11
二.信息熵
信息熵是每个事件的信息量乘它发生的概率,熵既有热力学概念,也有信息论的概念还有这哲学概念,它反应系统的混乱程度(不确定程度)
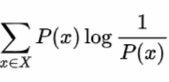
还以足球为例,中国对阵法国胜率为1%,法国有99%的概率会胜利,1%的概率会投降,所以中国队的胜率是1%,虽然中国队获胜这个事件信息量很大但是出现的概率低,所以对于总体的信息熵贡献不大
德国对阵比利时胜率各为1/2,虽然每个事件的信息量不大,但是乘以概率后总体的信息熵比较大,这个系统的信息熵是1,这也符合我们的直觉,这个系统相对于中国对阵法国的系统不确定性更大,信息熵也更大

用编码位数的方式来解释信息熵,它也可以这样被解释,对于一个概率分布P,描述P中事件的平均编码长度,当然,编码的长度不能带有小数,因为它代表了编码的位数,但是我们所说的信息熵是把这个情况从离散转移到连续的情况,由此引出交叉熵和相对熵(KL散度)的概念
三.交叉熵和相对熵
交叉熵刻画了使用错误分布Q来表示真实分布P中的样本的平均编码长度
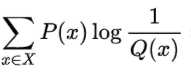
相对熵(KL散度)刻画了错误分布Q来表示真实分布P中的样本的平均编码长度的增量
从定义也可以看出相对熵 = 交叉熵 - P的信息熵

由吉布斯不等式可以证明,当使用错误的分布Q的编码来表示P时,总会比用P来编码P的长度更大,即相对熵总是个正值,它可以用来表示两个概率分布的差异(PQ和QP的KL散度是不一样的,不对称性)
![]()
这样我们就得到了两个重要的工具:
信息熵:描述概率分布的混乱程度,我们获取的信息越多,信息熵就越低
相对熵:描述两个概率分布的差异
由此引出它们在机器学习领域的应用:
四.条件熵
条件概率P(y|x)代表x条件下y发生的概率,条件熵也是如此,条件熵H(Y|X)表示在已知随机变量X的条件下随机变量Y的不确定性,但是H(Y|X)应当怎么求,能否仿照信息熵的公式,直接令条件熵为

显然是不可以的,我们说H(Y|X)表示在已知随机变量X的条件下随机变量Y的不确定性,而x不是已知的,即当x取不同值时,y的不确定性这个性质也是不同的,所以我们需要为上面的式子加一个权重p(x),那么式子就可以写成如下形式
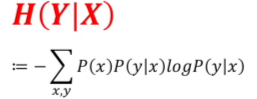
五.简介几个熵在机器学习领域的应用
1.决策树的属性选择基于信息熵,通过某个属性的划分更能够帮助对最终的结果进行预测,也就是更有助于降低信息熵,就认为这个属性对于最终的结果预测的帮助越大,这个属性就蕴含更多的信息
2.分类任务的损失函数可以使用交叉熵
分类器的输出一般是样本属于各个类别的概率,这个整体就是一个概率分布,而真实样本也可以理解成一个one-hot的概率分布,这两个概率分布的差异就可以用相对熵来表述,所以loss函数就可以使用相对熵,又因为相对熵 = 交叉熵 - 真实分布的信息熵,信息熵是一个固定值,所以我们就使用交叉熵作为loss函数。

除此之外,交叉熵的损失函数更加平滑,相对于MSE更能够帮助学习,它的等高线如图所示,红色代表loss大,蓝色代表loss小,可以看出交叉熵更加平滑

所以如果提问,为什么交叉熵适合做分类问题的损失函数?就可以这样回答
理论上:softmax输出的就是概率分布,KL散度恰好可以用来刻画两个概率分布之间的差异,而真实分布的信息熵是固定的,所以可用交叉熵可以当作损失函数
实际上:最后一层是softmax时损失函数是这样的,交叉熵里loss很大时梯度很大,MSEloss大时梯度很大,更大时反而梯度很小,是一个剧变,使用交叉熵更易收敛
3.最大熵模型
最大熵模型的思想:在满足已知条件的情况下,选取熵最大的模型;在满足已知条件前提下,如果没有更多的信息,则那些不确定部分都是“等可能的”,而等可能性通过熵最大化来刻画。
举个例子,8支球队参加世界杯,那每支球队夺冠概率是多少呢,我们在不知道任何信息的情况下,我们会觉得每支球队夺冠的概率都是1/8;但如果我们已知其中一支球队夺冠的概率是2%,那剩下7支球队就应该都是14%,即平分那98%的概率,实质上这就是最大熵的思想;后者因为已知了一个条件(其中一支球队夺冠的概率是2%),所以也可被称为条件最大熵。最大熵实质上就是为我们的直觉正名了,在机器学习中由已知(训练集)来预测未知(测试集)时,大部分模型实际上也是运用了这个思想
分类任务中的最大熵:
首先明确第一点:无论模型多么复杂,现在我们只考虑分类任务的最后一个全连接层,即从特征到类别的一层
第二点:对于我们分类任务的训练集,这个训练集里包含了一定的信息但不是能分类所有情况的信息,即训练集只能是样本空间的一部分,而不是样本空间的全部;所以机器学习的分类任务实质是基于两个先验假设:
第一个是“相同”的假设:我们得到的模型中应包含训练集的全部信息,即训练好模型以后再遇到与训练集相同的样本,模型得到的结果应当和训练集样本的标签一致。这就是最大似然的思想,也即交叉熵最小(如果目标是经验风险最小化那就默认勾选了这个假设)
第二个是“熵最大”的假设:分类任务要解决的问题本质上就是求P(y|x)的分布,x是样本空间里全部的样本,y是对应的标签,但是之前我们已经提到,我们无法得到全部的样本,那么对于未知部分,就要使其熵最大,这个熵是满足第一条假设时的条件熵(如果模型中使用了softmax或者sigmoid那就默认勾选了这个假设)
对于如何实现假设一,数学家们发明了一种很巧妙的方法——特征函数(指示函数)来解决这个问题(图源 王木头学科学)

由于这个概率分布是伯努利分布,而如果两个伯努利分布的一阶矩相等那这个两个概率分布就相等
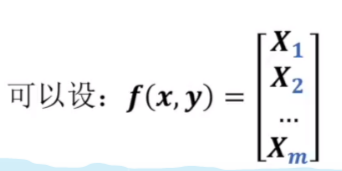
![]()
其中式子左边代表模型的特征函数对应f的一阶矩,右边代表训练集特征函数对应f的一阶矩
对于如何实现假设二,最大化条件熵,即
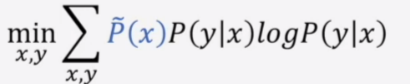
其中模型的x分布p(x)可以用![]() 代替,确保接下来的运算只有p(y|x)一个未知数,这也符合PAC的理念
代替,确保接下来的运算只有p(y|x)一个未知数,这也符合PAC的理念
于是我们要解决这样一个问题,满足如下两个前提的同时,最大化条件熵

于是可以使用拉格朗日乘数法求L的最小值
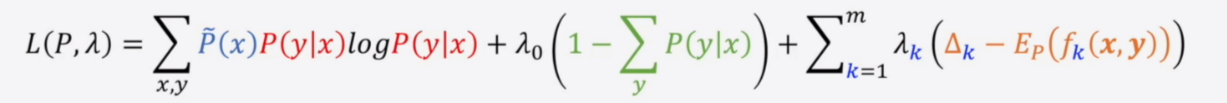
L对P(y|x)求偏导等于0,可解得
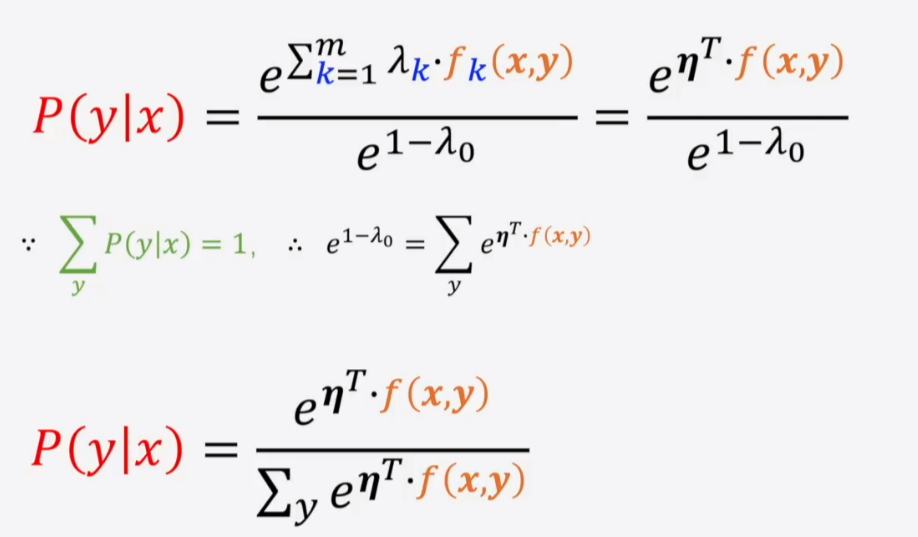
这就是softmax(sigmoid同理,二分类问题中另一个分类的输出为0就是softmax)
六.其他关于熵的思考
我听说过一个说法,一个耗散系统的演化是从低熵向高熵进行,还拿足球举例子,中国队对阵法国队目前胜率是1%,但是把这两个队天天放在一起训练,最后两者的胜率就会无限趋近于50%,就像溶液从高浓度流向低浓度一样,最后不是中国队把法国队带捞了,就是法国队把中国队带强了
你可能还听说过一个叫做二八定律的东西,20%的人掌握着社会80%的财富,把这种离散的模型迁移到连续的情况,这就是帕累托分布(这是一个厚尾模型,它的u均值在采样无限时可以趋于无限大)从如下的图像可以看到,采样时大部分样本都聚集在前面,但采样足够多时,总有x非常大的样本来影响采样数据整体的分布,这个概率分布的熵值就很低

与帕累托分布相比,正态分布的熵值就非常大,这也对应了事物演化的开始和结局;有一种说法,宇宙诞生时是符合帕累托分布的,它的熵值很低,也具有很大的活力;宇宙热寂时,它的熵值很大,符合正态分布,也就是说事物的发展过程就是从幂律分布到正态分布

还拿二八定律举例,我们目前社会的财富比例符合二八定律,大部分财富在少部分人手中,但它最终必将演化到正态分布,大部分财富掌握在大部分人手中,这时社会形态就从资本主义演化到共产主义,我们又从信息论的理论证明了马克思主义的正确性
以上即是我对机器学习里信息论内容的理解,如有批评与补充,不胜感激。




