数据挖掘中的常见数据预处理方法总结

一.基本概念

为什么需要数据预处理：

现实世界中数据大体上都是不完整，不一致的脏数据，无法直接进行数据挖掘，或挖掘结果差强人意。为了提高数据挖掘的质量产生了数据预处理技术

数据：数据对象及其属性的集合

属性值是分配给属性的数字或符号

属性和属性值的区别 – 相同的属性可以映射到不同的属性值

      　　　　　　　  – 不同的属性可以映射到同一组值

属性值的类型：

属性的类型取决于它拥有以下哪些属性：独特性（可以判断等于和不等）；顺序；加法；乘法

标称属性：独特性

序数属性：独特性和顺序

区间属性：独特性、顺序和加法(比如温度)

比率属性：所有 4 个属性（比如长度）

数据集的类型：

记录数据，图数据，顺序数据

顺序数据举例：

基因组序列数据；

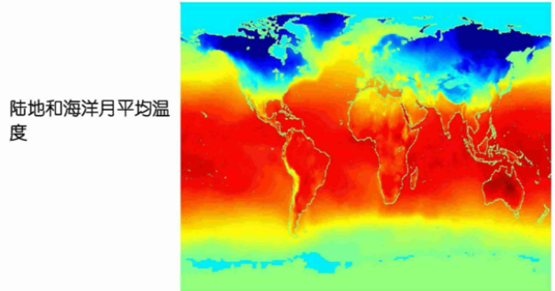
时间-空间数据：

 

属性的模式（众数）是出现频率最高的属性值

百分位数：对于连续数据，百分位数的概念更有用，给定一个有序或连续的属性 x 和一个 0到100 之间的数字p，第p个百分位数是一个值 x 使得 p%的值小于 x 的观测值

第二个四分位数 = 第 50 个百分位数 = 中位数

第三个四分位数 = 第 75 个百分位数

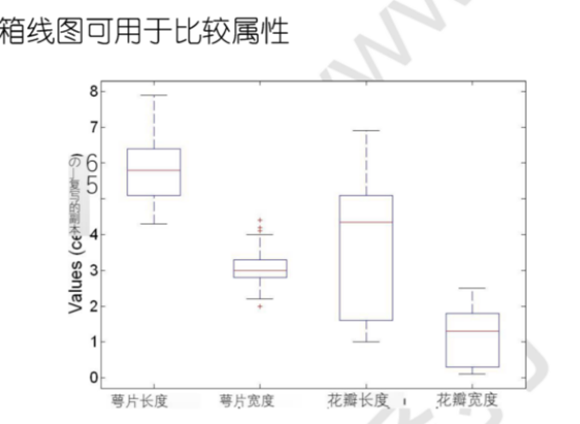
五数总结法：最低 – 第 1 个四分位数 – 中位数 – 第三个四分位数 – 最大值，可用箱形图表示

 

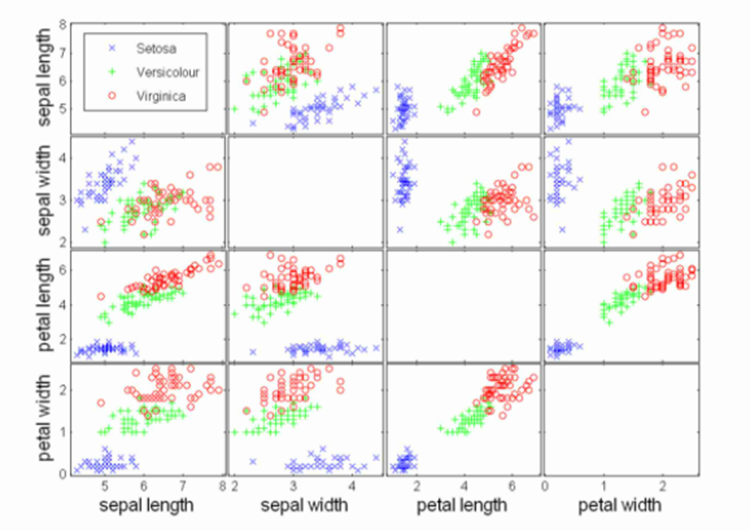
散点图：属性值两两配对作图，可用于发现属性间的关系

 

 

 

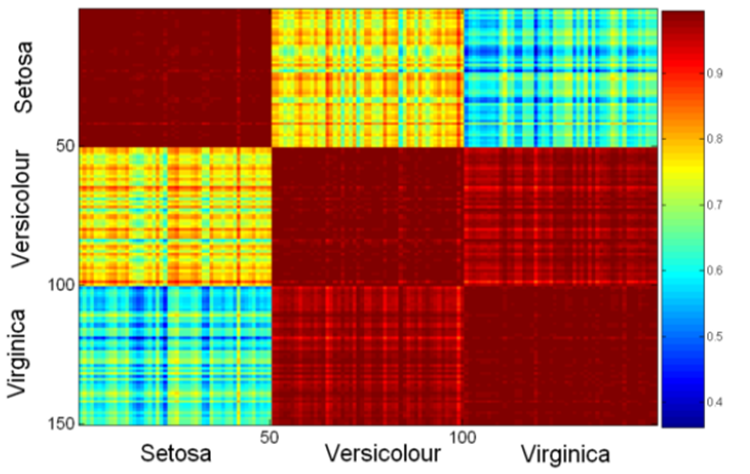
矩阵的每个值是其行坐标与列坐标的相似性

平行坐标图：

 

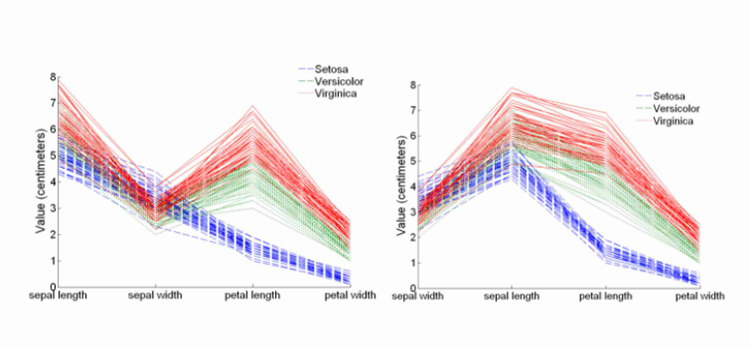
每一条折线代表一个实例，横坐标是不同的属性

数据质量问题：

噪音：噪声是指对原始值的修改

异常值：异常值是具有与数据集中的大多数其他数据对象显着不同的特征的数据对象

缺失值

重复数据

数据质量的衡量标准:

● 准确性：正确或错误，准确与否

● 完整性：未记录、不可用、……

● 一致性：一些修改但一些没有，悬空，

● 及时性：及时更新？

● 可信度：数据正确的可信度如何？

● 可解释性：数据有多容易被理解？

数据预处理

数据清洗

清理缺失数据： ●忽略元组：通常在缺少类标签时完成（进行分类时）——当每个属性的缺失值百分比变化很大时无效 ● 手动填写缺失值：乏味+不可行？ ● 自动填写 – 一个全局常量：例如，“未知”，一个新类 – 属性均值 – 属于同一类的所有样本的属性均值：更聪明 – 最可能的值：基于推理，如贝叶斯公式或决策树 – 替换为所有可能的值（按概率加权） 清理噪声数据 ： ● 分箱 – 首先对数据进行排序并将其划分为等频箱 – 然后可以通过分箱方法平滑，比如通过分箱中值平滑， 通过分箱边界平滑等。 举例： 价格的排序数据（以美元计）：4, 8, 9, 15, 21, 21, 24, 25, 26, 28, 29, 34 划分为等频（等深度）箱： - 箱 1：4、8、9、15 - 箱 2：21、21、24、25 - 箱 3：26、28、29、34 按 bin 平滑意味着： - 箱 1: 9, 9, 9, 9 - 箱 2：23、23、23、23 - 箱 3: 29, 29, 29, 29 按 bin 边界平滑： - 箱 1: 4, 4, 4, 15 - 箱 2：21、21、25、25 - 箱 3：26、26、26、34 ● 回归 – 通过将数据拟合到回归函数中来平滑 ● 聚类 ● 结合计算机和人工检查 清理不一致的数据更复杂 ● 使用依赖，比如函数依赖 ● 使用人工编译的规则 识别或移除异常值

数据集成	多个数据库、数据立方体或文件的集成（不介绍）

数据缩减

概念：获得数据集的缩减表示，该表示的数量要小得多，但仍会产生相同（或几乎相同）的分析结果

为什么要减少数据？ 数据库可能存储数 TB 的数据。复杂的数据分析可能需要很长时间才能在完整的数据集上运行

维度诅咒：如果您在单位正方形中随机选择一个点，它与边界距离小于 0.001 的几率只有 0.4%，可以计算这个值在单位线段时是0.2%，单位立方体时是0.6%，在一个 1000 维的单位超立方体中，这个概率大于 99.999999%，因此高维超立方体中的大多数点都非常靠近边界。如果您考虑足够多的维度，那么您认识的任何人都可能是至少一个维度的极端分子。当维数增加时，数据在它占据的空间中变得也越来越稀疏，这样对聚类和异常值检测至关重要的点之间的密度和距离的定义变得没有意义。

数据缩减策略

降维：   数据处于或接近低维子空间，用矩阵表示的话，秩就是维度 数量减少 数据压缩 ：降维和数量减少也可以被认为是数据压缩的形式，此外还有字符串压缩，音视频压缩

数据转换	归一化：缩放到更小的指定范围内 – 最小-最大归一化   – z-score 归一化   – 十进制归一化         属性/特征构建 – 从给定的属性构造的新属性 聚合：汇总、数据立方体构建 离散化：概念层次爬升 分箱，直方图分析，聚类分析，决策树分析，相关性分析 分箱（简单离散化方法）： 等宽分箱，将范围分成大小相等的N个区间（均匀网格） 等深度（频率）分箱，将范围划分为 N 个区间，每个区间包含大约相同数量的样本 离散区间的大小影响支持度和置信度 – 如果间隔太小,可能没有足够的支持 – 如果间隔太大,可能没有足够的置信度 可能的解决方案：使用所有可能的间隔 平滑：从数据中去除噪声

二.常见数据降维方法

（1）主成分分析

PCA的本质：

一是，要考虑去除掉特征之间的相关性，想法是创造另一组新的特征来描述样本，并且新的特征必须彼此之间不相关。

二是，在新的彼此无关的特征集中，舍弃掉不重要的特征，保留较少的特征，实现数据的特征维度降维，保持尽量少的信息损失

一种PCA的方法：

第 1 步：将数据集围绕原点居中

 

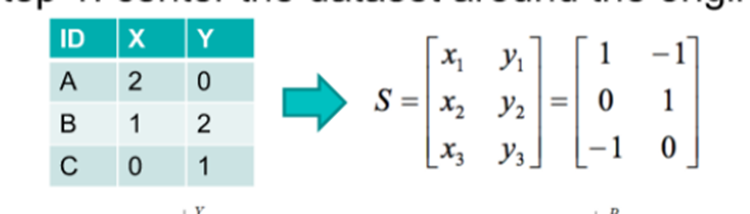
第 2 步：计算 STS

 

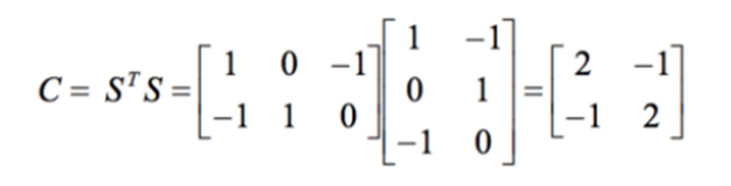
第 3 步：找到 C 的特征值和特征向量

 

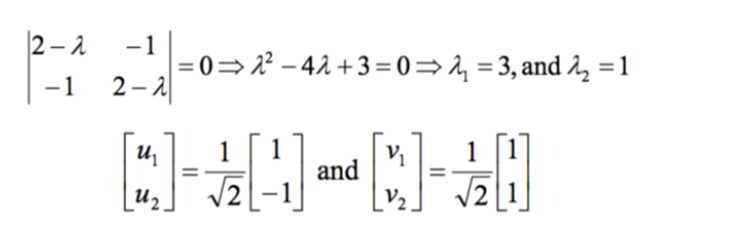
第 4 步：将数据集投影到新空间

 

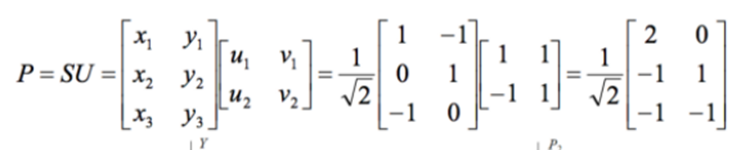
然后可以把方差最小的那个维度去掉

该算法的解释：（不同特征值对应的特征向量线性无关，对于实对称阵是正交的）

 

SVD4PCA:

SVD也是对矩阵进行分解，但是和特征分解不同，SVD并不要求要分解的矩阵为方阵。假设我们的矩阵A是一个m×n的矩阵，那么我们定义矩阵A的SVD为：

 

 

V（右奇异向量）的列是 ATA 的特征向量

U（左奇异向量）的列是 AAT的特征向量

Σ的对角线上的元素（奇异值）是 ATA（或 AAT(只是相差了几个0)）的特征值的平方根

这里我们用一个简单的例子来说明矩阵是如何进行奇异值分解的。我们的矩阵A定义为：

 

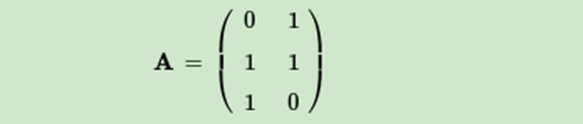
首先求出 

 

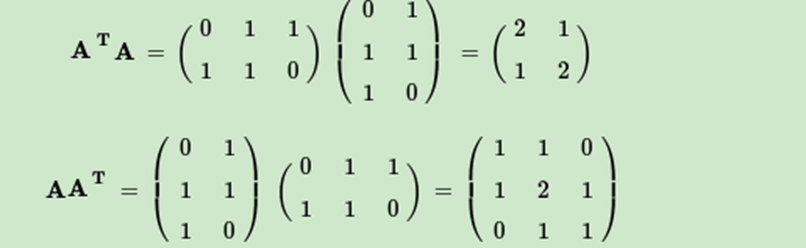
进而求出ATA的特征值和特征向量：

 

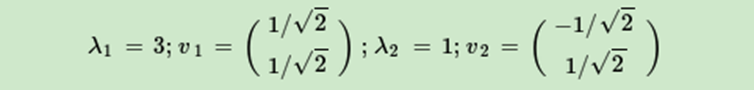
接着求出AAT的特征值和特征向量：

 

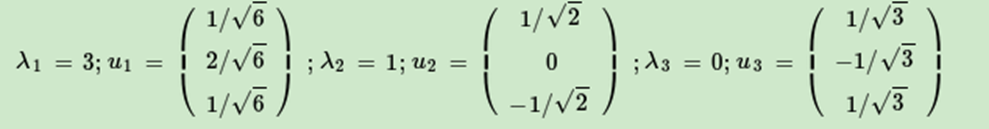
最终得到A的奇异值分解为：

 

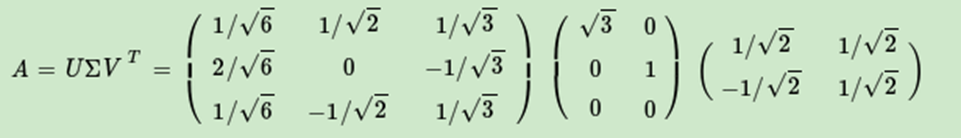
对于奇异值,它跟我们特征分解中的特征值类似，在奇异值矩阵中也是按照从大到小排列，而且奇异值的减少特别的快，在很多情况下，前10%甚至1%的奇异值的和就占了全部的奇异值之和的99%以上的比例。

也就是说，我们也可以用最大的k个的奇异值和对应的左右奇异向量来近似描述矩阵。

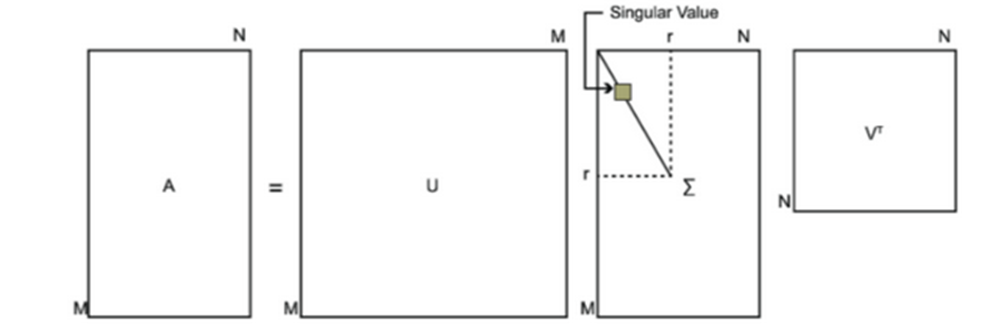
如下图所示，现在我们的矩阵A只需要灰色的部分的三个小矩阵就可以近似描述了。

 

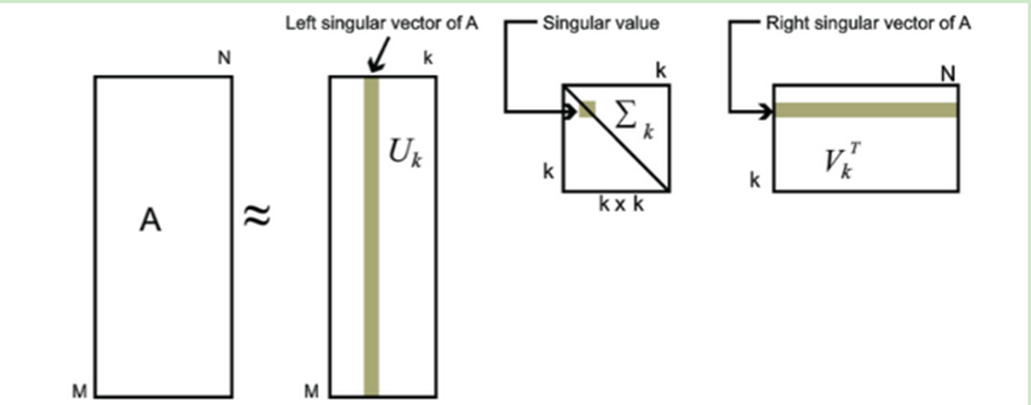
由于这个重要的性质，SVD可以用于PCA降维，来做数据压缩和去噪。也可以用于推荐算法，将用户和喜好对应的矩阵做特征分解，进而得到隐含的用户需求来做推荐。同时也可以用于NLP中的算法，比如潜在语义索引（LSI）。

左奇异矩阵可以用于行数的压缩。（UΣ，即左边两个矩阵相乘）

右奇异矩阵可以用于列数即特征维度的压缩，也就是我们的PCA降维。(ΣVT，即右边两个矩阵相乘)

SVD作为一个很基本的算法，在很多机器学习算法中都有它的身影，特别是在现在的大数据时代，由于SVD可以实现并行化，因此更是大展身手，SVD的缺点是分解出的矩阵解释性往往不强，有点黑盒子的味道，不过这不影响它的使用。

（2）属性子集选择

属性消除：

冗余属性  – 例如，产品的购买价格和支付的销售税金额

不相关的属性 – 例如，学生的 ID 通常与预测学生 GPA 的任务无关

属性创建（特征生成）：创建新的属性（特征），可以比原始属性更有效地捕获数据集中的重要信息

– 属性提取：在特定领域

– 将数据映射到新空间，例如，傅里叶变换、小波变换（未涵盖）

– 属性构建：组合特征（判别频繁模式），数据离散化

三.计算向量之间的相似性

（1）简单匹配法和jaccard（p和q在各个属性维度只能取0和1）

 

（2）余弦相似度

 

二元属性：取值为0或者1的属性，所以也成为布尔属性

对称二元属性：属性的两个状态的权重相同，例如：“性别”这一属性的取值“男性”，“女性”。

非对称二元属性：即状态的权重不相同，例如：“HIV”有“阴性”和“阳性”，阳性比较稀少，更重要。

有时属性有许多不同的类型，但需要整体相似性，使用以下方法：

 

可以理解为非对称属性上两个向量取相同值，在相似度上应该有更小的说服力

四.计算属性的相关性

相关不意味着因果（比如一个城市的医院数量和汽车盗窃数量是相关的，两者没有直接的因果，但两者都与第三个变量有因果关系：人口）

（1）Pearson 相关系数

衡量两个数值属性之间的相关性：

 

性质：

 

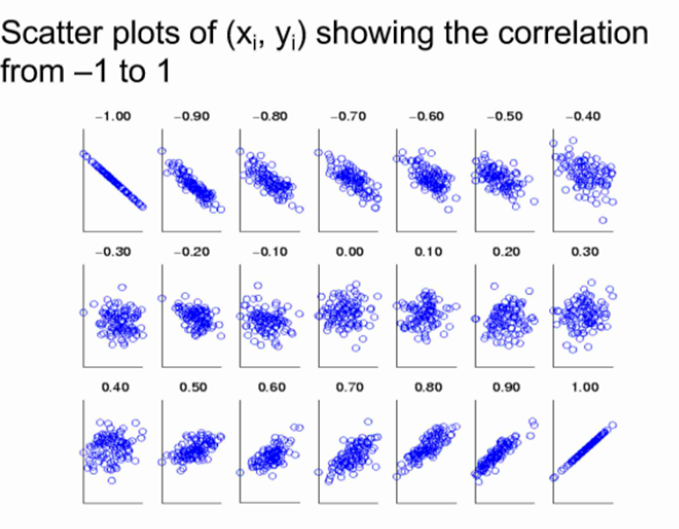
相关系数仅衡量线性相关性，它可能完全错过非线性关系

 

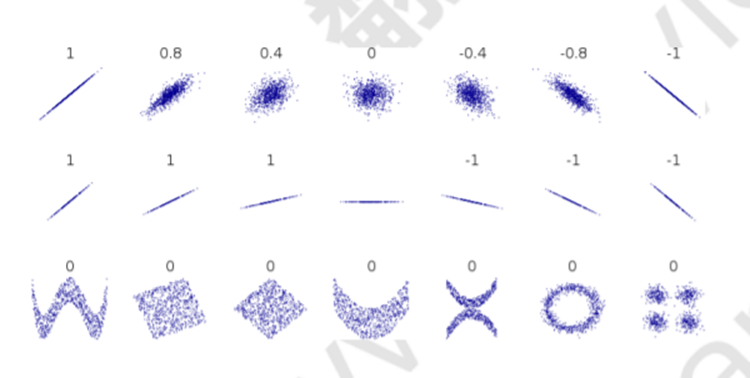
其中，相关性为1和-1时与其斜率无关

方差：

 

（2）卡方统计

不同于卡方检验，衡量两个标称属性之间的相关性：

Cij是属性x=xi且属性y=yj的对象数量，卡方越大相关性越强，自由度(m-1)(n-1)