------------恢复内容开始------------
------------恢复内容开始------------
------------恢复内容开始------------
------------恢复内容开始------------
作业信息
作业要求:https://www.cnblogs.com/rocedu/p/9577842.html#WEEK07
作业目标:自学《计算机科学概论》第八章、《c语言程序设计》第六章
作业正文:
教材学习内容总结
一、《计算机科学概论》
第八章:
抽象数据类型
抽象数据类型,简称ADT,他将由数据和操作构成的属性和特定实现分离,每个ADT存有特定行为时就变成了容器
栈
栈,最为重要的特点就是后进先出,也就是只有一个入/出口,如该伪代码执行后的结果是倒序的而并非正序输入的顺序
队列
队列,则是与栈相反,他讲究的是后进后出,再如该伪代码执行后的结果与上面结果则是相反的
列表
列表,列表的列是无穷的,他有三个属性特征:项目是线性的、同构的、变长的,同时需要注意的是列表不是数组,数组是内嵌结构,数组内可以应用列表,有无序算法区别在于输出顺序的不同
树
树,是个较大的概念,包含很多“小树”,有二叉树,二叉检索树,和有关树的一系列算法,二叉树是一种比较常见的抽象概念,包含唯一的根节点和各种子节点,每个节点可以有左右子树,根节点与子节点之间只有一个路径,一种特殊的节点是叶节点,他是没有子女的树节点;
二叉检索树,二叉检索树树与二叉树的区别在于他的节点存在语义排序,并且存在严格的规定,任何节点的树必须比左子树的数大,比右子树的数小;在树中的搜索也是在检索树中完成的,给出一个数,先于根节点比较,初步判断位置大面上的左右子树,然后再从相应位置继续与相应的根节点比较,以此类推,所以存在一个搜索算法用于搜索;但若没有二叉检索树的情况下,则需要自己构建一个,基本的原则就是插入值按照检索树的规则来进行排序,需要用到insert函数来实现插入,在输出的时候也采用相同的递归算法,达到目的的同时又实现了简短精致;
图
图,某种意义上可以看作是解除了节点数量限制的树,在此基础上,有一组组节点和节点间的线段构成,节点叫做顶点,线段叫做边,顶点表示对象,边表示了对象之间的关系,所以图又可以分为有向图和无向图,无向图的边没有方向,有向图则是固定的由某一方向指向另一个方向;
图的创建,可以从构建表格开始,先添加顶点,再添加边,最后添加权值;
图的算法,有关图的算法有三种,深度优先搜索、广度优先搜索、单源最短路搜索;
深搜DFS,遵循按深度最大来进行,选择一条路尽可能深入,走到头,就是说该点没有其他节点了,再回退到上一个节点,继续探索该节点的其他支路,就该支路继续深入,以此类推的遍历方法;
广搜BFS,遵循范围最大的原则来进行,按照层级结构,一层一层来进行,完成第一层的遍历后,再进行第二层,第三层...依此类推,最终遍历完成,将所有元素都过了一遍;
单源最短路搜索,需要与权值有关,是经计算后的每个路径的权值和进行比较,然后挑选出一个权值最小的路径,其中需要用到迪杰斯特拉算法颇有难度,但同时这种搜索在如今的生活中应用的也是最多最广的,像诸多地图软件中的两点距离路径的寻找,则就可以将地图抽象为一张图,然后进行单源最短路搜索即进行其他算法与迪杰斯特拉算法的结合,得出结论
二、《C语言程序设计》
第六章:
循环
while
while语句中的循环控制表达式是在执行循环体之前进行测试的,执行前需先进性括号内表达式true false的判断
do-while
do-while语句中的循环判断条件是在执行后进行的,不论条件的真假,都要先进行一次循环体语句。在使用时,也许格外注意这一点
for
for循环是写出程序过程中,应用最多的,基本形式为括号内有三种语句,由两个分号隔开,第一个为循环变量及其初始化,第二个是循环控制的条件,第三个是循环变量的增量,由以上三者决定了循环的次数,
其余的循环
计数控制的循环,事先知道循环次数的循环叫计数控制循环,累加累乘求和的问题就是需要用到他来实现;嵌套循环,虽然会增大时空复杂度,但是可以处理多层次的问题以及减少过多的重复代码;条件控制的循环,循环次数未知的循环由一个条件控制叫条件控制
流程的转移控制
goto
goto是无条件的语句,功能极其强大,可以向任意方向跳转,但虽表示无条件跳转,但一般与if连用,也可以不用,如在实验二中我使用到goto实现无条件的跳转进行错误数过多重新计算的步骤
break
break可以用作退出所有循环的语句,只要碰到他,循环立刻停止,
continue
continue与break的区别在于,continue在于跳出当前本次循环,整体循环并不终止,重新返回上方重新进行
三,基于AI的学习
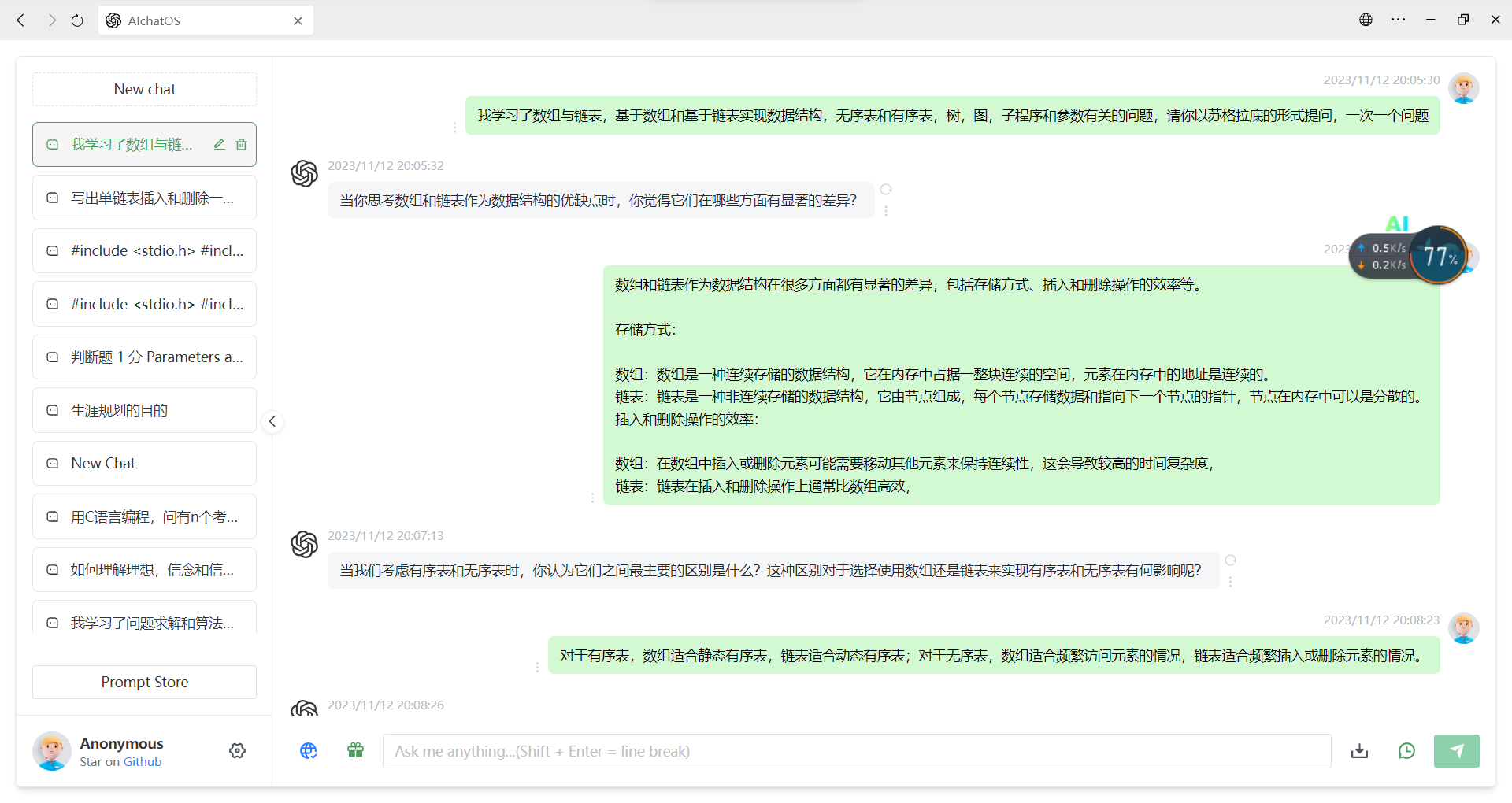
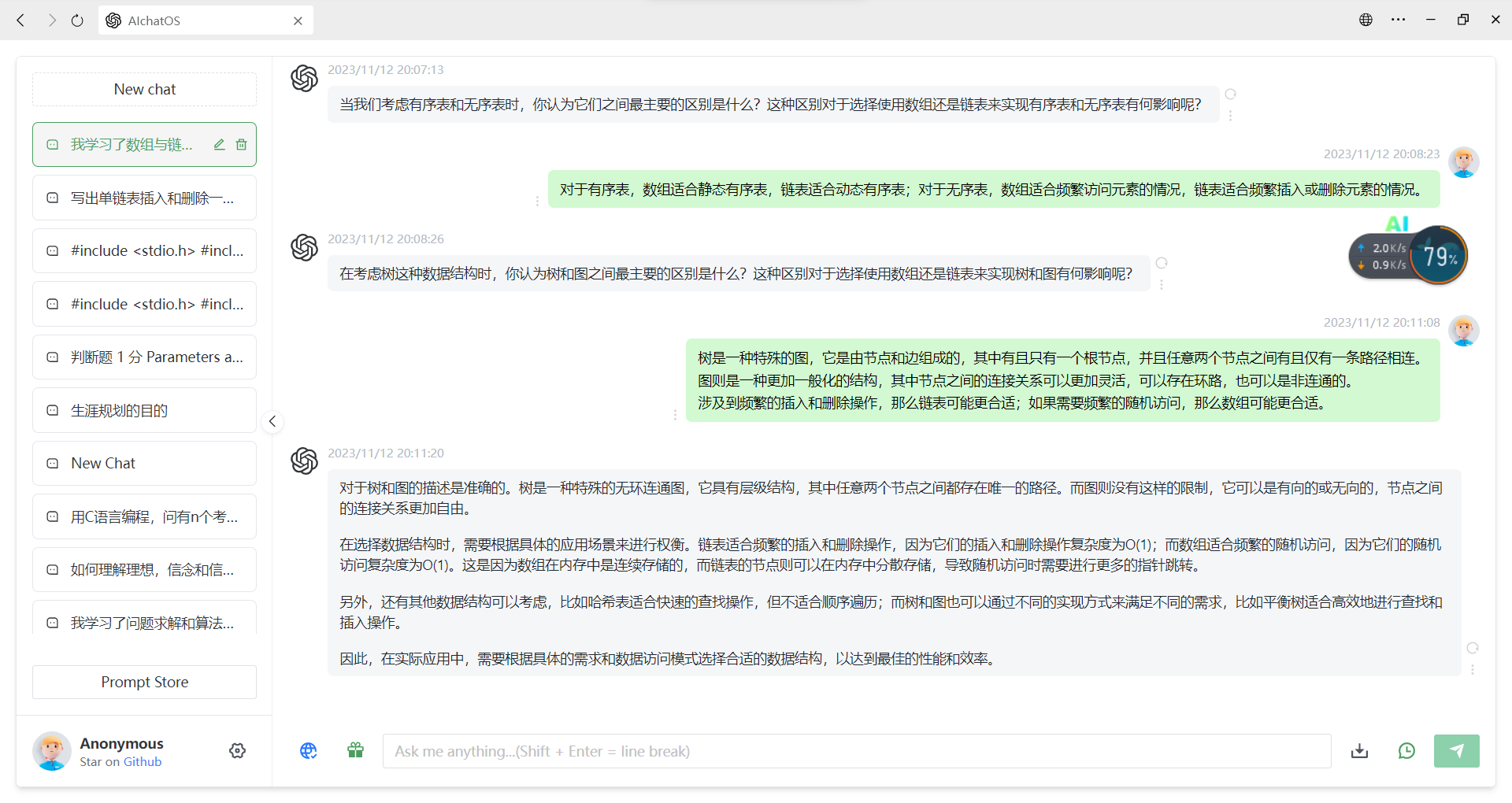
学习进度条
| 代码行数 | 博客数 | 学习时间 | |
| 目标 | 5000 | 30 | 400 |
| 第一周 | 200/200 | 2/2 | 20/20 |
| 第二周 | 300/300 | 4/4 | 28/28 |
| 第三周 | 500/500 | 6/6 | 30/30 |
| 第四周 | 500500 | 8/8 | 30/30 |
| 第五周 | 600/600 | 9/9 | 35/35 |
| 第六周 | 800/800 | 10/10 | 40/40 |
| 第七周 | 1000/1000 | 12/12 | 45/45 |
------------恢复内容结束------------
------------恢复内容结束------------
------------恢复内容结束------------
------------恢复内容结束------------



