心里有红黑树

Why 红黑树

为什么大家都这么推崇红黑树呢? 这就是数据结构的魅力!!! 下面我简述一下常用数据结构的优缺点

• 数组

大家对数组很熟悉, 都知道对数组来说,它底层的存储空间是连续的,因此如果我们根据index去获取元素,速度是相当快, 但是对于数组来说有时候查询也不见得就一定块, 比如我们查询数组中名字叫张三的人, 也不得不从开始遍历这个数组

如果我们想往数组中插入一个元素, 也不见得一定就慢, 比如我们往数组中最后的位置插入就很快, 但是要是往开始的位置插入的话, 肯定会很慢, 需要将现有数组中所有的元素往后移动一位, 才能空出开始的位置,给新元素用

• 链表

一说链式存储, 大家也都知道, 这种数据结构仅仅是逻辑连续, 物理存储不连续, 因此我们有可以通过玩指针或者引用很快的完成元素的删除和添加

对链表的查询来说, 一定是慢的, 无论查询谁, 查哪个, 都得从第一个节点开始遍历

• AVL树

AVL树, 就是二叉平衡树, 这种有序的树形结构就将链式存储添加删除快, 顺序存储的查找快两大有点进行了一次中和, 在绝大部分情况下, AVL树在增删改查方面的性能都原超过数组和链表

• 红黑树

红黑树是对AVL树是又一次重大升级, AVL树,对于树的平衡要求太严格了, 每当添加,删除节点时,都不得不进行调整

对于红黑树来说, 每次添加一个新的节点都是最多进行两次旋转(左旋右旋)就能重新使树变的平衡,

但是当我们删除一个叶子节点时, AVL树重新调整成平衡状态时最多需要进行旋转O(logN)次, 而红黑树最多旋转3次就能重新平衡,时间复杂度是O(1)

还有就是红黑树并不是完全意义上的AVL树, 也就是说它其实并不是真的像AVL树那样严格要求对一个节点来说左右子树的高度差不能超过1, 而是选择使用染成红色和黑色进行维护

简单来说, 因为红黑树并不像AVL树那样完全平衡, 可能会导致红黑树的读性能略逊于AVL, 但是红黑树的维护成本绝对是远远低于AVL, 在空间上的开销和AVL树基本持平, 因此红黑树被大家极力推崇, 和学习java的同学直接相关的就是jdk8的 hashmap

红黑树的特性

红黑树主要存在下面的7条性质

1. 节点非红即黑
2. 根节点必定是黑色
3. 叶子节点全部是黑色, (这里说的叶子节点是我们想象在肉眼看到的节点上再多加一层子节点)
4. 红节点的子节点必定是黑色
5. 红节点的父节点必定是黑色
6. 从根节点到任意子节点的路径上,都要经历相同数目的黑节点
7. 从根节点到任意子节点的路径上不可能存在两个连续相同的红节点

常见的误区

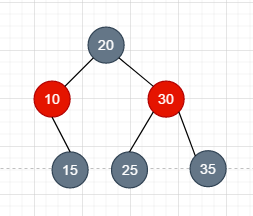
如上图, 看着挺像红黑树, 其实他不是, 看它node10, 并不满足上面的性质6. 因为我们认为node10的左子节点是黑色的节点, 这样的话, 从node20到node10的左子节点就经历了两个黑节点, 而其他的 node15, node25, node35 经历的黑色子节点数都是三个

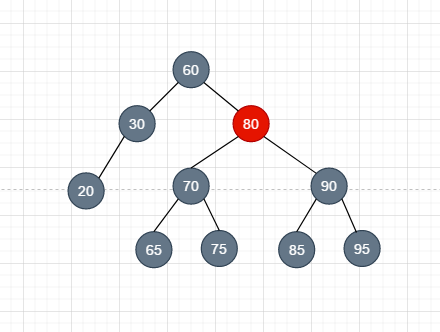
如上图它也不是红黑树, 因为我们认为node30的右节点是黑色的节点, 这样的话从node60到node30的右节点就经历了三个黑色的节点, 而其他的所有子节点都经历了4个, 故, 他不是红黑树

红黑树与2-3-4树等价

如上图中,当我们将一个红黑树中的黑色节点和红色节点融合在一起时,我们会发现, 这个红黑树其实就是一颗2-3-4树, 一颗四阶B树

并且, 红黑树中黑色节点的每一个合并完成后的节点中都有一个黑色的节点, 换句话说就是红黑树中黑色节点的个数等于2-3-4树中节点的个数

添加

添加节点其实就是构造红黑树的过程, 只要我们严格遵循上面的7条限制, 构造出来的树就是红黑树

通过上图其实我们发现, 红黑树真的可以和四阶B树之间进行等价代换, 换句话说就是 4阶B树的性质对于红黑树来书其实也是存在的, 主要是如下两条性质

• 所有新添加进去的节点都被放在了叶子节点上
• 2-3-4树中每一个节点中允许承载的元素的个数 [1,3]

经验推荐: 就是新添加的节点尽量全部是红色, 如果你画一画就会发现, 如果我们新添加的节点是红色的话,上面所说的7条性质中, 除了第四条(红节点的子节点必定的黑节点). 其他的限制都可以满足

---

于是看一下一颗四阶B树插入节点时有哪些种情况

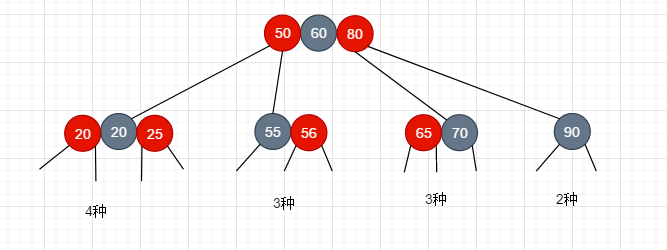
数一数: 一共 4+3+3+2 = 12种情况, 换句话说, 只要我们处理好了这12种情况, 我们就完成了添加节点的逻辑

• 情况1, 就是假设我们添加进去的是红色的节点, 并且这个红色节点的父节点是黑色节点时, 直接添加进行,不需要其他任何变换, 就想下图这样, 直接简单粗暴的添加就行

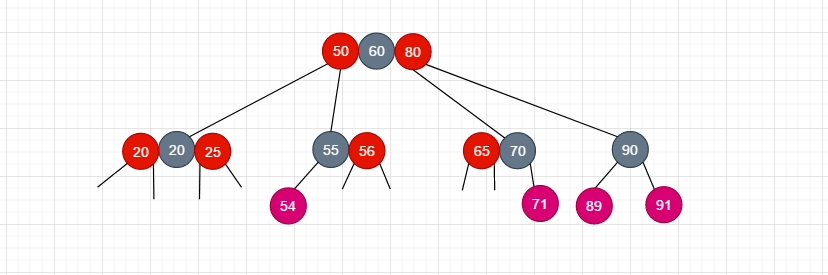
除去第一种情况外, 还剩下8中情况出现了红红节点相邻, 于是继续往下看, 我们对他进行一次修复

• 情况2: 如下图

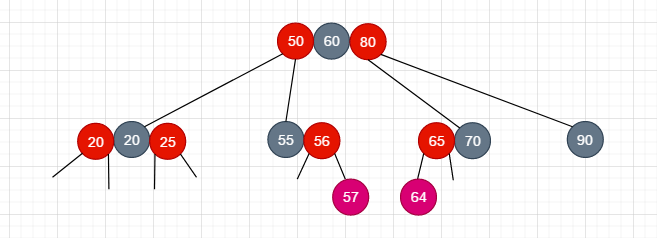
插入的node57, node64, 什么情况呢? 就是当前节点是node5556, 首先这个节点中现存两个元素, 并且是往这个黑色的节点的左侧的左侧插入, 或者是右侧的右侧插入一个红色节点

看上图出现了两个红色节点相邻,于是我们第一件事就是进行重新染色,

1. 将插入节点的父节点染成黑色
2. 将插入节点的祖父节点染成红色
3. 将祖父节点进行旋转, 如果这个新节点被插入在父节点的右侧. 左旋转它的祖父节点

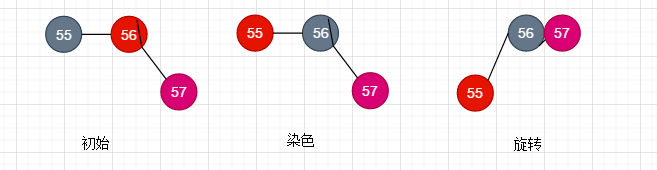
经过上面的变换后, 我们重新得到标准的红黑树如下

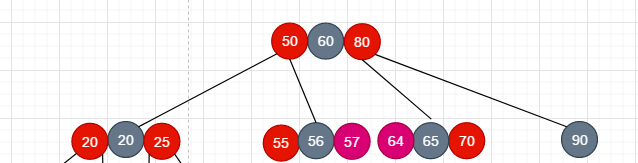
• 情况3: 新添加的节点的叔叔节点不是红色

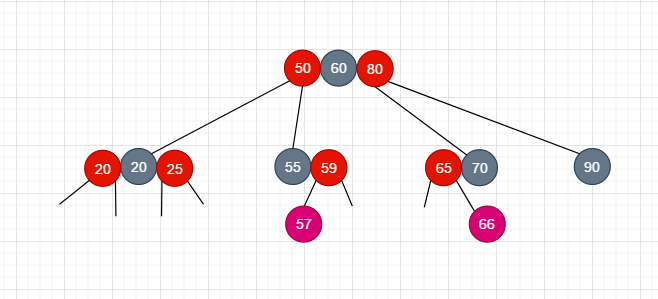
第三种情况和第二种情况相似, 还是插入 node57和node64. 判断的条件是 插入节点的叔叔节点(父节点的兄弟节点)不是红节点,

简称 LR , 或者是RL , 需要进行如下的调整

1. 染色: 将自己染成黑色,祖节点染成红色
2. LR: 父节点左旋转, 祖父节点右旋转
3. RL: 祖父点右旋转, 父节点左旋转

LR举例:

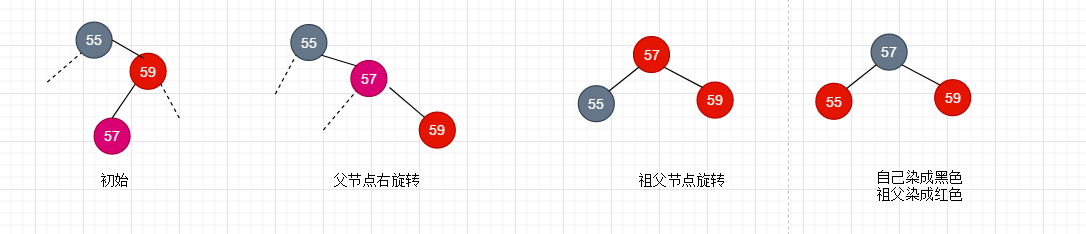
经过上面的变化,我们重新得到平衡的红黑树

---

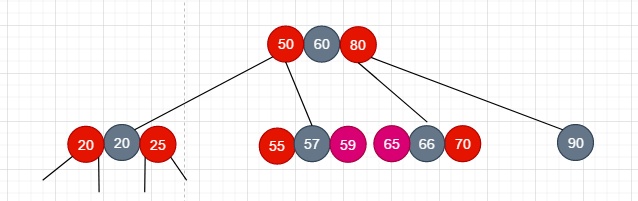
接着往下看剩下的四种情况

• 情况4: 新添加的节点的叔叔节点是红色, 其实就是需要上溢的情况, 也很好处理

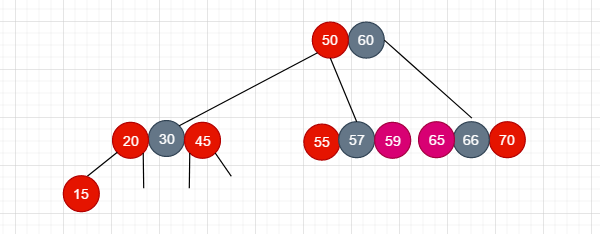
像上图这样, 新添加的红色节点 node15, 它本身的父节点是node20, 父节点的叔叔节点是红色的node25, 我们比较node15和node20的大小, 发现node15本来是应该放在node20的左边的, 但是对于一颗2-3-4树来说, 单个节点最多就有3个元素, 如果再加上node15 就会出现上溢的情况, 怎么办呢? 我们上溢调整, 选择这个节点中间位置的元素向上和父节点合并, 选择node20, node30其实都是可以的, 为了方便我们选择node30

好,下面开始修复这个红黑树

1. 将插入的节点的父节点和它的叔叔节点染成黑色
2. 发生了上溢, 将他的父节点的染成红色, 递归插入到根节点上, 这时候根节点可能又会发生上溢

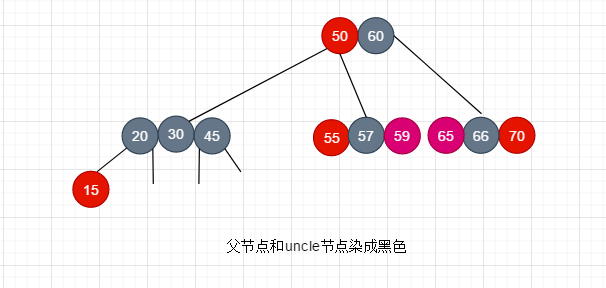
然后上溢

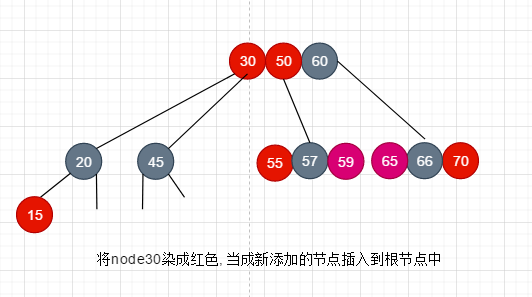
当我们将新插入的节点的父节点node30染成红色时, 再插入到根节点, 实际上就是重复我们枚举出来的这12种情况中的一种. 红黑树一定会被修复, 当然这时候很可能会出现根节点也容纳不了新的元素, 需要根节点也进行上溢, 然后将根节点染黑

还有一种情况是像下面这样, 同样是在情况4下的新插入的节点的叔叔节点是红色

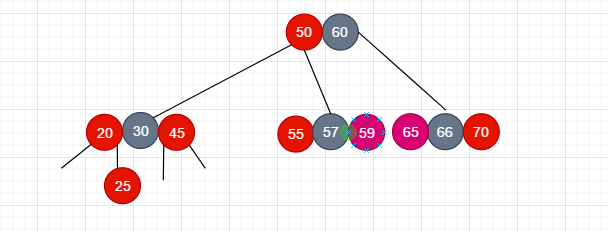
像下面这样调整:

1. 将父节点和叔叔节点染成黑色
2. 祖父节点上溢

然后就是这种情况

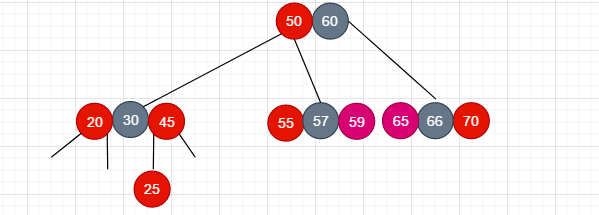
调整的思路和前面一样

1. 将父节点和叔叔节点染成黑色
2. 将祖父节点上溢

至此红黑树的添加的12种情况就全部枚举完成了

删除

对于删除来说总共两大种四小种情况

• 第一种就是删除的节点就是红色节点, 如果真是这样的话,直接删除就ok
• 第二种是删除的节点是黑色节点
  • 删除拥有1个red节点的黑色节点
  • 删除拥有2个red节点的黑色节点,
  • 删除黑色节点

如果一个像下面这样, 下面的黑色节点有两个子节点, 这种情况下,黑色节点肯定不会直接被删除的, 需要进行变换,让他的叶子节点去替换他,进而实现删除的目的

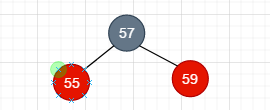
• 情况1: 删除拥有1个红节点的黑色节点,像下图这样

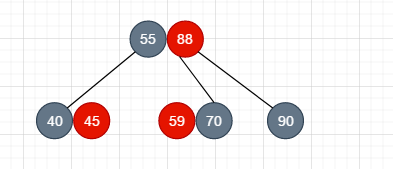
怎么判断这就是我们想删除的情况呢? 当我们确定用来替代这个被删除的黑节点是红色,则符合当前的情况

也就是说我们想删除 node40 和 node70, 于是我们这样做

1. 让这个指向被删除的节点的指针指向这个被删除的节点的子节点
2. 将替代它的节点染成黑色

于是我们接得到下图这样的结果

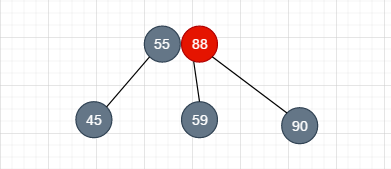
• 情况2: 删除的节点是黑色的叶子节点, 并且可向兄弟节点借

首先,如果这个叶子节点就是根节点的话,直接删除就ok

看下面的这个图, 我们就删除其中node90， 即，删除黑色叶子节点

如果想删除上图中的node90也是由窍门的，规律和2-3-4树是擦不多的

假设它就是2-3-4树， 如果我们将node90删了， 我们计算一下， 对于2-3-4树来说， 每一个节点位置上至少有 ⌈ 4/2 ⌉ -1 = 1个元素， 但是把node90删除了这个位置上的节点中没有元素， 因此产生了 下溢

出现下溢，我们首先考虑的情况就是看看可不可以向它的兄弟节点借一个，但是和B树是有取别的， 多了下面的限制

1. 被删除的这个节点的兄弟节点必须是黑色的
2. 被删除的这个节点的兄弟节点一定的有红色的子节点才ok， 就像上图那样， 可以在左边，右边，或者都有
3. 直接删除掉指定的node（因为它在叶子节点的位置上）
4. 进行旋转，旋转时注意， 两点：第一点： 比如下面的原来根节点位置上的元素88是红色的， 经过旋转上来替换它的节点的颜色必须染成红色， 如果node88是黑色， 那么经过旋转上来替换他的节点的颜色必须染成黑色 ，第二点： 旋转完成后，新的跟节点的直接左右子节点的颜色转换为黑色

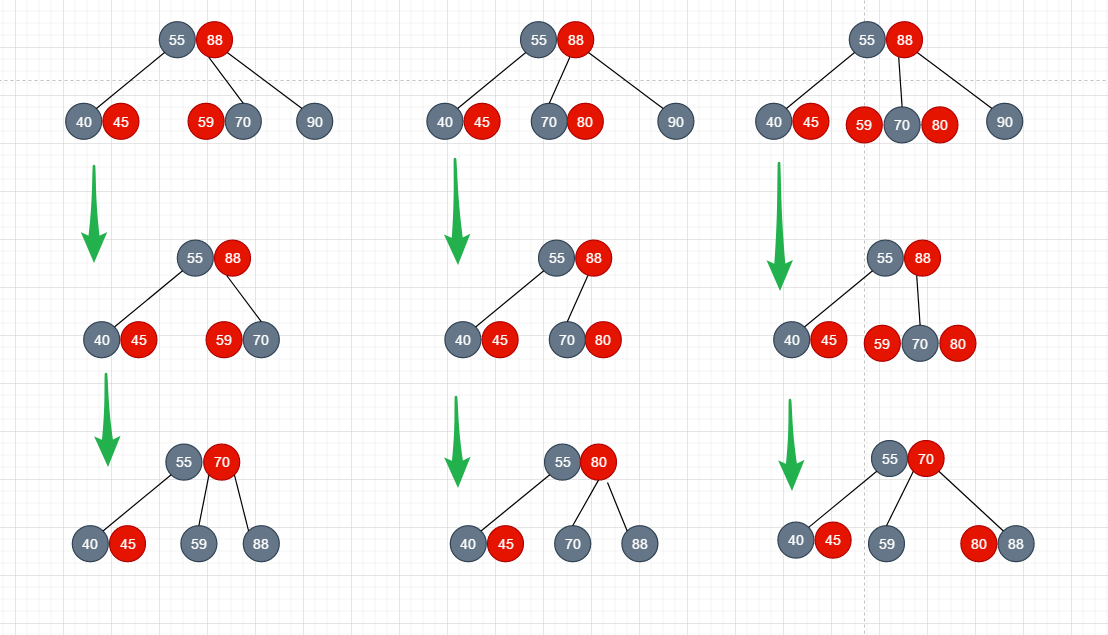
怎么进行旋转呢？ 就像下图这样

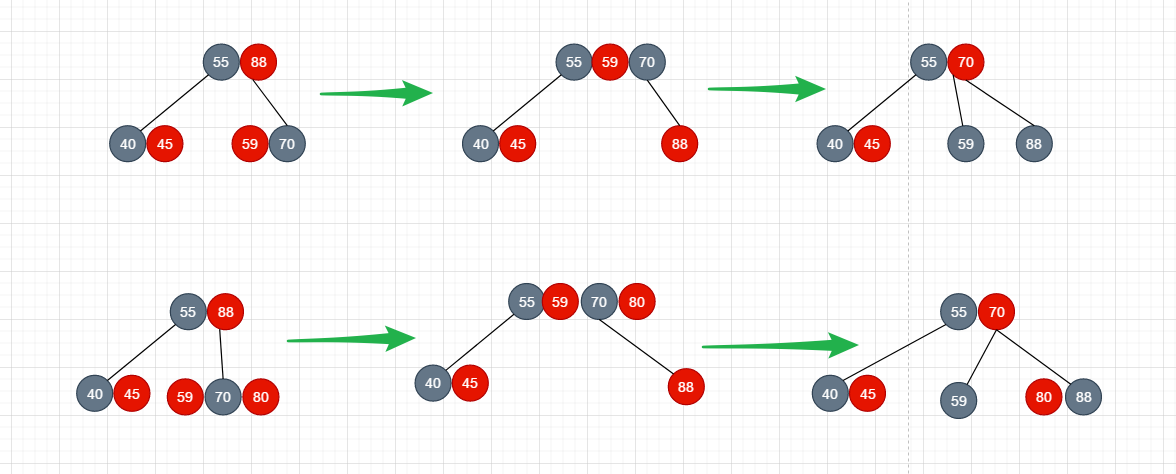
• 情况3: 删除的节点是黑色的叶子节点, 并且它的兄弟是黑色，而且它的兄弟节点不能借给他元素

像这种情况：我像删除node99，但是没办法像他的兄弟节点借元素，于是

1. 将父节点向下合并,父节点染成黑色
2. 将它的兄弟节点染成红色

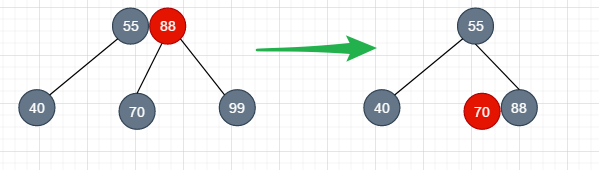
也有特殊的情况, 就是它的父节点只有一个,还是黑色

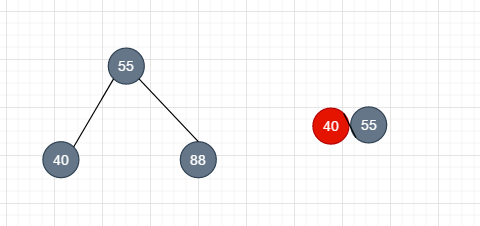
这时候,我们将他的父节点下溢, 原位置的节点舍弃

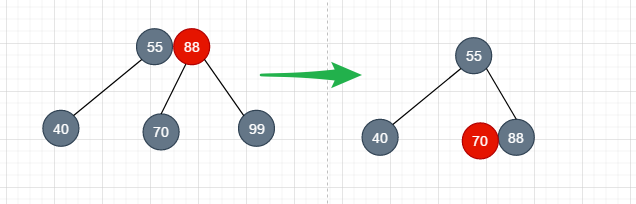
• 还有最后一种情况就是, 删除的是黑色的节点, 它的兄弟节点的是红色的节点

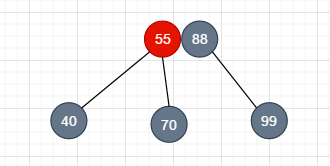
就像上图那样,我们想删除node99, 但是node99的兄弟节点其实是node55, 而不是node77, 我们怎么样才能转换为前面说的那些情况呢?

1. 将被删除节点的父节点染成红色, 兄弟节点染黑

2. 让被删除的父节点进行右旋转(node88右转)

   得到下图

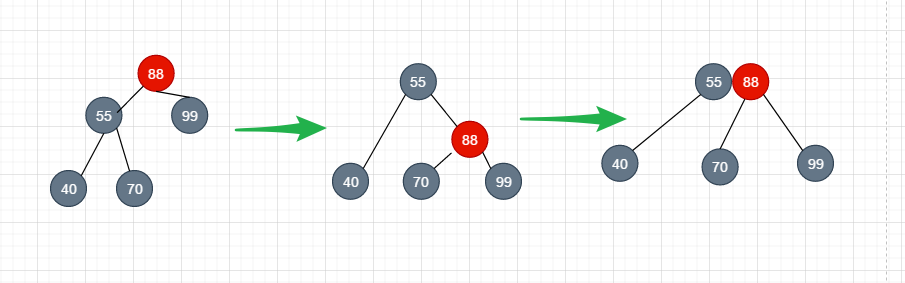
于是我们就将这种兄弟节点为红节点的情况转化成了兄弟节点为黑色节点的样子, 按照原来的方式进行删除修整即可

3. 让原父节点下溢
4. 原染成黑色
5. 兄弟节点,染成红色

至此本文就结束, 欢迎关注我,后续我更新更多的关于开发相关的笔记