计算机的运算方法
计算机的运算方法
无符号数
计算机中的数存放在寄存器中,通常将寄存器的位数称为机器字长, 大家说的无符号数其实就是不区分正负号的数,换句话说,就是没负数,全是正数,大家知道,计算机中的数是以0-1存储的, 假如我们的寄存器16位, 无符号数表示的范围就是0~65535 (2^64=65536), 有符号就是分正负数,总数65536就被分成两半,一半正数,一般负数,范围就是 -32768~32767
有符号数
有符号数,就是正负数同时存在, 人们固然能区分开整正负数,计算机怎么区分呢?
前面说了,计算机只认识01这样的数,于是人们规定 0表示正数, 1表示负数, 于是这样符号就被数字化了, 并且规定将其放在真实值前面, 于是有符号数就诞生了
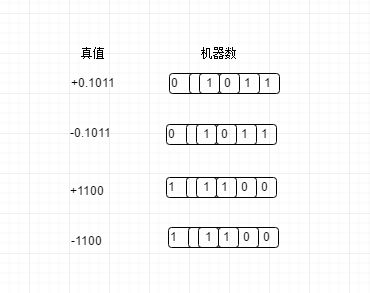
如上图,按照计算机存数数据的特性将符号数字化, 数字化后的编码方式得到的结果称为机器数, 将带有+-符号的数字称为真值
既然现在将有符号数数字化后,新的问题来了,当这些机器数之间需要进行运算时, 符号位怎么办? 符号位能否参加机器数之间的运算呢? 如果说,需要参加运算又需要哪些处理才能消除符号位对计算结果的影响呢? **这一连串问题就引出了符号位和数值位所构成的编码: 原码 , 补码 , 反码 , 移码 **
其实在学习的过程中该一直问自己,自己在干什么??? 就比如现在,我在前面大概说了说计算机是如何表示数字的,于是认识了机器码,机器码之间需要进行运算于为了设计出使机器码运算的方式,人们对机器码进行不同的变形编码,得到了,原码 , 补码, 反码 , 移码等, 下面看一下这几种编码的由来,以及他们对实现机器码的可计算的贡献
原码
原码是机器码最简单的一种变形,同样的它的符号位0表示正数,1表示负数。 数值位就是真值的绝对值
人们为了书写方便已经区分小数和整数,在符号位和数值位之间使用逗号分隔
整数的原码
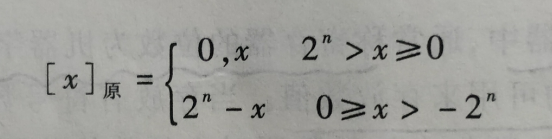
举个例子:
x= +1110, 那么它的原码就是 0,1110
x= -1110, 原码=1,1110
小数的原码
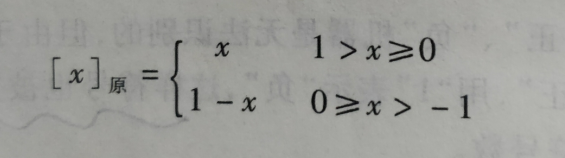
举个例子
x= 0.1101 , 那么它的原码就是 0.1101
x= -0.1101, 原码=1 - (-0.1101) = 1.1101
看上面的原码计算方式,显然机器码很容易就转成原码,但是想想如果用原码进行数值运算的话就会带来很多麻烦,我们得先判断两个机器数绝对值的大小然后用大的减去小的,最终的符号再按照绝对值大的算, **而且我们需要设计两套运算流程,一套给加法用,一套给减法用, 但是前辈们很智慧,因为人们找到了一种方式,找到了一个正数去替换原来减数位置的负数,类似像下面这样,实现了在计算机中仅仅设计一套加法器就实现加减法的运算 **
5-3=2
5+(-3)=2
上述方法的实现就依赖于下面的补码
补码
补码的概念和补数的概念很像, 比如现在时钟六点了,我们想让它指向三点,于是我们可以往回转3(6-3=3)圈时针能回退到3点,也可以往前转9圈(6+9=15),可以前进到三点, 对时钟来说往顺时针还是逆时针的过程不一样,但是对我们来说结果是一样的,都是三点了
这个过程就类似于,找到一个正数,让这个正数代替负数去参加运算,使用加法运算器也能得到正确的结果
时钟旋转一圈12小时,在这12小时中是不被显示且自动丢失的,也就是说 15-3=3 点, 于是我们可以说,其实对时钟来说, -3 +9 的作用其实是一致的,结果都是三点, 在数学上我们将12称为模 ,写成mod 12 , 我们管9 称为是 -3以12为模的补数
于是我们得知,只要我们确定了模,我们就能求出这个数对这个模的地位相同的补数,或者说当我们想将已知的负数转换成可以替换他的正数的话,借助模就可以完成
如何利用模求补数呢?
- 正数的补数是它本身
- 负数可以用它的正补数等价替换
- 负数的补数= 模+负数本身
如何进行求模示例:
-3 全等于 +7 (mod10)
+7 全等于 +7 (mod10)
-3 全等于 +97 (mod100)
-1011 全等于 +0101 (mod2^4)
2^4=1 0 0 0 0
- 1 0 1 1
---------------
0 1 0 1
+0101 全等于 +0101 (mod2^4)
小数的mod = 2
+0.1001 全等于 +0.1001 (mod2)
-0.1001 全等于 +1.0111 (mod2)
1 0.0 0 0 0
- 0.1 0 0 1
--------------
1.0 1 1 1
求补码的公式

求负数补数的示例

其实大家可以看一下,对负数的公式来说,公式中的n就是负数的位数, -1101 一共四位, n=4, 但是取的是n+1位, 换句话说是用一个比原负数多两位的数加上这个负数, 多出来一个符号位, 最后的结果中别忘了用 逗号分隔符号位和数值位, 当然这是为了方便我们自己看,让人们一眼看去知道最开始的1是个符号位,后面的数才是 想求的补数结果
小数求补码的公式
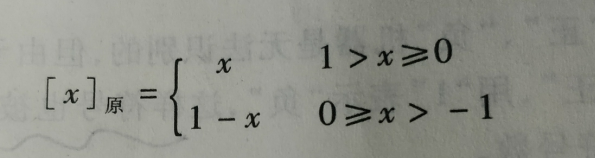
举个例子: 求 -0.0110 的补码
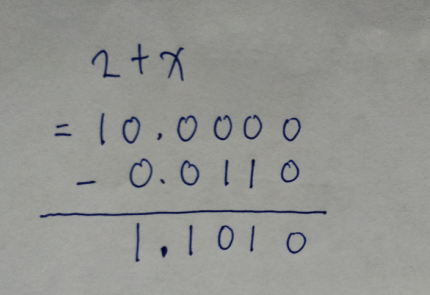
此外, +0 -0的补码都是 0
从上面的讨论我们知道,之所以想引入补码是为了消除减法运算,即将一个负数转换成它的正数补码,但是根据补码的定义,大家可以看到上面的两个例子,在产生补码的过程中又出现了减法运算,怎么办呢?
于是我们这样求补码: 先求原码, 然后变换这个原码得到补码, 怎么变换呢? 就是将除了 符号位的原码其它为取反 之后再加1
举个例子: 上面的就用 -1101 来说, 如下:
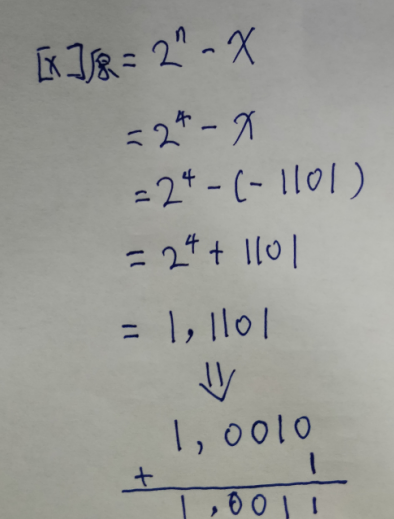
于是看到这里我们彻底知道了,只为计算机设计一个加法器是完全ok的,下文会介绍如何运算
反码
通过上面的运算我们知道下面的运算规则
原码(符号位,数值位) => 除符号位外其他位取反 = 反码
反码+1 = 补码
补码-1 = 反码
由此可知,其实这个反码就是原码和补码双方转换时的中间状态
小结
- 原码,反码,补码的最高位都是符号位, 符号位和数值位之间使用.或者逗号分隔(小数用点, 整数用逗号)
- 真值为整数时, 原码,反码,补码的表示形式是相同的
- 虽然真值为负数时,原码.反码补码各不相同,但是最高位的符号为都是1, 并且原码求反+1=补码 , 原码每位求反=反码
移码
真值转换成补码后,由于符号位和数值位是一起进行编码的,因此人们很难分清补码之间的大小
就像下面这样
十进制的21 对应二进制为+10101 补码为 0,10101
十进制的-21 对应二进制为-10101 补码为 1,01011
十进制的31 对应二进制为 +11111 补码为 0,11111
十进制的-31 对应二进制为-11111 补码为 1,00001
直观上看他们的大小是 101011>010101 100001>011111 而实际上恰恰相反
于是我们这样, 在每一个真值的基础上加上一个2^n , 情况就发生了变化
+10101 加上2^5 得 110101
-10101 加上2^5 得 001011
+11111 加上2^5 得 111111
-11111 加上2^5 得 000001
这样的话不需要借助补码,六位代码本身就能看到出真值的大小
更进一步,通过观察可以发现,其实一个数的补码和移码之间就差一个符号位,换句话说,如果我们将补码的符号位从0换为1,或者从1换成0得到的就是它的移码, 在这基础上比较大小得到的结果是准确的
此外正负零的移码的一样的
移位运算
计算机中的机器数的字长往往是固定的,当机器数左移n位或者是又移n位时,势必会倒是另外一边出现空位,那么在出现空位的位置到底是补充1还是填充0呢? 这取决于机器数是有符号还是无符号,其中有符号的机器数采取的位移称为算数位移,无符号的唯一称为逻辑位移
算数位移的移位规则
| 真值 | 码制 | 补填代码 |
|---|---|---|
| 正数 | 原码,补码,反码 | 0 |
| 负数 | 原码 | 0 |
| 负数 | 原码 | 左移添0 |
| 负数 | 补码 | 右移添1 |
| 负数 | 反码 | 1 |
无论是正数还是负数,移位后的符号位都是不变的
举几个例子
机器数 十进制
移位前 : 0,0011010 +26
左移1位: 0,0110100 +52
右移1位: 0,0001101 +13
左移一位,除符号位外原来的最高位被移走了,右边空出的1位用0补全,但是高位丢失了其实得到的就是错误的结果,但是这个错误的结果恰好是原值的2倍,而且唯一运算速度还快,因此很多框架的底层都青睐使用这个位移运算的特性
每次右移时,最右边的数就会丢失,精度收到影响
左移一位相当于乘以2,右移1位相当于除以2
逻辑位移的移位规则
逻辑左移,高位丢失,低位填0, 逻辑右移,低位丢失,高位补0
加法与减法运算
回到一开始话题,计算机的运算方法,前面通过补码的介绍我们知道了只设计一套加法器其实是可行的,下面具体看一下是如何进行运算的
即 A-B = A + (-B)
补码的加法公式
整数: [A]补 + [B]补 = [A+B]补 (mod 2^n+1)
小数: [A]补 + [B]补 = [A+B]补 (mod 2)
对于减法来说
整数: [A-B]补 = [A]+[-B]补 (mod 2^n+1)
小数: [A-B]补 = [A]+[-B]补 (mod 2)
最后看一个例子: 看看计算机如何将减法转换成加法并携带符号位运行得出正确结果
假设机器8位(含一位符号位),若A=+15 B=+24, 让我们求 [A-B]补 ,并还原真值
A=+15 = +0001111 (算上+号一共八位)
b=+24 = +0011000 (算上+号一共八位)
A和B都是整数,所以他们的补码就是原码本身:
[A]补 = 0,0001111
[B]补 = 0,0011000
[-B]原码 = 1,0011000
[-B]反码 = 1,1100111 ( 除符号位取反得到反码:)
[-B]补 = 1,1101000 (由反码+1得到)
[A-B]补 = [A]补 + [-B]补
= 0,0001111 + 1,1101000
= 1,1110111
那么 A-B = 啥呢? 反着换回去
1,1110111
1,1110110 (末位减1再取反)
1,0001001 = -0001001 = -9


 浙公网安备 33010602011771号
浙公网安备 33010602011771号