距离度量方法
1.曼哈顿距离(Manhattan Distance)
定义：在欧几里德空间的固定直角坐标系上两点所形成的线段对轴产生的投影的距离总和。
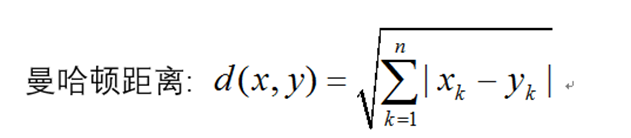
想象你在曼哈顿要从一个十字路口开车到另外一个十字路口，驾驶距离是两点间的直线距离吗？显然不是，除非你能穿越大楼。实际驾 驶距离就是这个“曼哈顿距离”,也称为城市街区距离(City Block distance)。
2.欧式距离(Euclidean Distance)
定义：欧几里得距离或欧几里得度量是欧几里得空间中两点间“普通”（即直线）距离。
欧式距离是一个通常采用的距离定义，指在m维空间中两个点之间的真实距离，或者向量的自然长度（即该点到原点的距离）
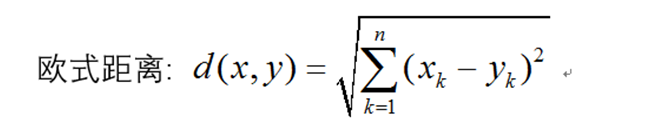
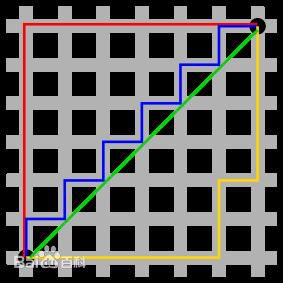
图中红线代表曼哈顿距离，绿色代表欧式距离，也就是直线距离，而蓝色和黄色代表等价的曼哈顿距离。
3.切比雪夫距离(Chebyshev distance)
定义：切比雪夫距离是向量空间中的一种度量，二个点之间的距离定义是其各坐标数值差绝对值的最大值。
4.闵可夫斯基距离(Minkowski Distance)
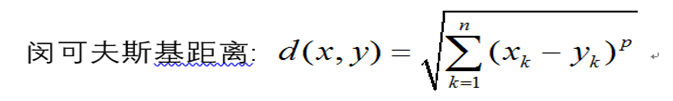
其中p是一个变参数。
当 p = 1 时，就是曼哈顿距离
当 p = 2 时，就是欧氏距离
当 p → ∞ 时，就是切比雪夫距离
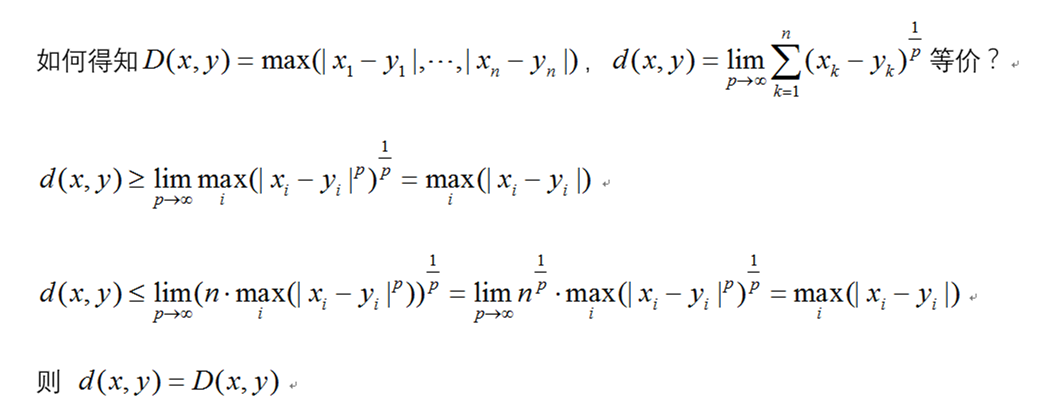
闵可夫斯基距离比较直观，但是它与数据的分布无关，具有一定的局限性，如果 x 方向的幅值远远大于 y 方向的值，这个距离公式就
会过度放大 x 维度的作用。所以，在计算距离之前，我们可能还需要对数据进行 z-transform 处理，即减去均值，除以标准差（即 标准化欧式
距离）。
这种方法在假设数据各个维度不相关的情况下利用数据分布的特性计算出不同的距离。如果维度相互之间数据相关（例如：身高较高的
信息很有可能会带来体重较重的信息，因为两者是有关联的），这时候就要用到马氏距离（Mahalanobis distance）了。
5. 标准化欧式距离(Standardized Euclidean distance)
思路：既然数据各维分量的分布不一样，那先将各个分量都“标准化”到均值、方差相等。假设样本集 X 的均值(mean)为 m ，标准差(standard deviation)为 s ， X 的“标准化变量”表示为：
则标准化后的欧式距离公式为：
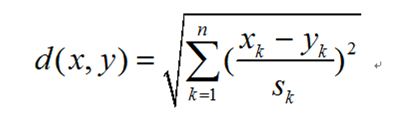
如果将方差的倒数看成一个权重，也可称之为加权欧氏距离(Weighted Euclidean distance)
6.马氏距离(Mahalanobis distance)
马氏距离表示数据的协方差距离，是一种有效的计算两个未知样本集的相似度的方法。其计算是建立在总体样本的基础上的。即，它考虑到各种特性之间的联系，是尺度无关的（独立于测量尺度）。
一原始多维样本数据 Xnm ( m 维，n 个样本 X=(X1, X2,...,Xn))：
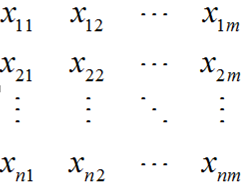
对于一个样本的总体均值为μX=(μX1,μX2,...,μXm)，其协方差为Σ，的多变量矢量X=(X1, X2,...,Xn)T，其到样本中心 u 的马氏距离为：
而马氏距离也可以定义两个服从同一分布并且其协方差矩阵为Σ的两个随机变量的差异程度：
如果协方差矩阵为单位矩阵，马氏距离就简化为欧氏距离。
而马氏距离如何不受到量纲的影响呢？
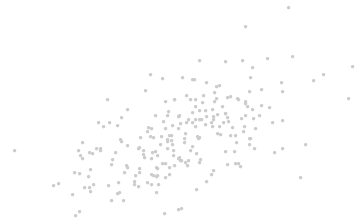
1. 下图为二元数据的散点图：
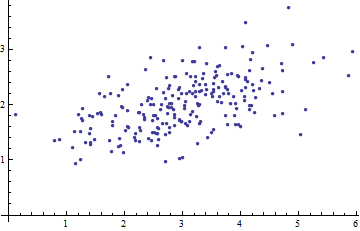
将坐标拿掉以后，如下图：
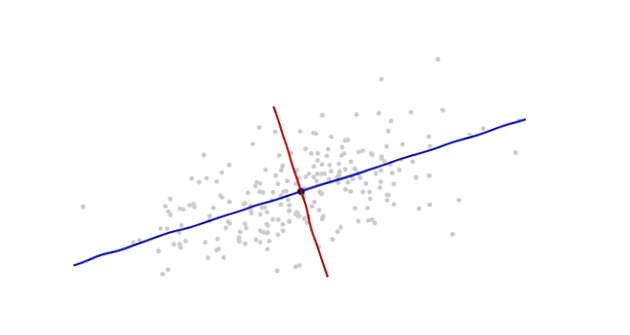
2. 根据数据本身的提示信息来引入新的坐标轴。 坐标的原点在这些点的中央（根据点的平均值算得）。第一个坐标轴（下图中蓝色的线）沿着数据点的“脊椎”，并向两端延伸，定义为使得数据方差最大的方向。第二个坐标轴（下图红色的线）会与第一个坐标轴垂直并向两端延伸。
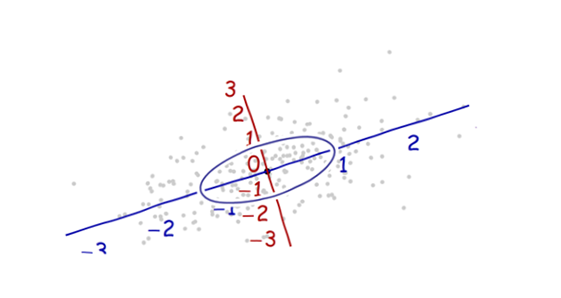
3. 然后，我们需要一个比例尺度。用数据沿着每一个坐标轴的标准差来定义一个单位长度。要记住68-95-99.7法则：大约2/3的点需要在离原点一个单位长度的范围内；大约95%的点需要在离原点两个单位的长度范围内。
4.让我们重新沿着正确的方向画图——从左到右，从下到上（相当于旋转一下数据）。同时，并让每个轴方向上的单位长度相同，这样横坐标上一个单位的长度就与纵坐标上的单位长度相同。
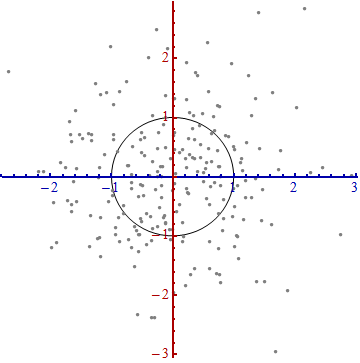
假设数据分布是一个二维的正椭圆，x 轴 y 轴均值都为0，x轴的方差为1000，y轴的方差为1，考虑两个点 (1, 0) ， (0, 1) 到原点的距离，如果计算的是欧氏距离那么两者相等，但是仔细想一下，因为x轴的方差大，所以 (0, 1) 应该是更接近中心的点，也就是正态分布标准差的 (68, 95, 99.7) 原则。这时候需要对 x , y 轴进行缩放，对应的操作就是在协方差矩阵的对角上加上归一化的操作，使得方差变为1。 假设数据分布是一个二维的椭圆，但是不是正的，比如椭圆最长的那条线是45°的，因为矩阵的对角只是对坐标轴的归一化，如果不把椭圆旋转回来，这种归一化是没有意义的，所以矩阵上的其他元素（非对角）派上用场了。如果椭圆不是正的，说明变量之间是有相关性的（x 大 y 也大，或者负相关），加上协方差非对角元素的意义就是做旋转。
马氏距离，欧式距离，标准化欧式距离小结：
1. 欧式距离
2. 标准化欧式距离：能够体现各个特性在变差大小上的不同，同时，距离与各个特性所用单位无关
3. 马氏距离 ： 各种特性之间的联系（如身高与体重）
马氏距离的计算是建立在总体样本的基础上的，如果拿同样的两个样本，放入两个不同的总体中，最后计算得出的两个样本间的马氏距离通常是不相同的，除非这两个总体的协方差矩阵碰巧相同。
在计算马氏距离过程中，要求总体样本数大于样本的维数，否则得到的总体样本协方差矩阵逆矩阵不存在，这种情况下，用欧氏距离计算即可。
满足了条件总体样本数大于样本的维数，但是协方差矩阵的逆矩阵仍然不存在，如三个样本在其所处的二维空间平面内共线。这种情况下，也采用欧氏距离计算。
7.余弦相似度(Cosine Similarity)
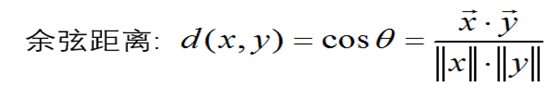
余弦相似度更多的是从方向上区分差异，而对绝对的数值不敏感。因此没法衡量每个维数值的差异，会导致这样一个情况：比如用户对内容评分，5分制，X 和 Y 两个用户对两个内容的评分分别为(1,2)和(4,5)，使用余弦相似度得出的结果是0.98，两者极为相似，但从评分上看 X 似乎不喜欢这2个内容，而 Y 比较喜欢，余弦相似度对数值的不敏感导致了结果的误差，需要修正这种不合理性，就出现了调整余弦相似度，即所有维度上的数值都减去一个均值，比如 X 和 Y 的评分均值都是3，那么调整后为(-2,-1)和(1,2)，再用余弦相似度计算，得到-0.8，相似度为负值并且差异不小，但显然更加符合现实。
8.汉明距离(Hamming Distance)
两个等长字符串 s1 与 s2 的汉明距离为：将其中一个变为另外一个所需要作的最小字符替换次数。
9.杰卡德距离(Jaccard Distance)
杰卡德距离(Jaccard Distance) 是用来衡量两个集合差异性的一种指标，它是杰卡德相似系数的补集，被定义为1减去Jaccard相似系数。而杰卡德相似系数(Jaccard similarity coefficient)，也称杰卡德指数(Jaccard Index)，是用来衡量两个集合相似度的一种指标。
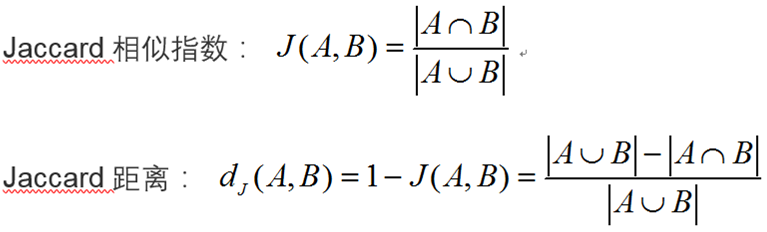
10.皮尔逊系数(Pearson Correlation Coefficient)
在统计学中，皮尔逊相关系数，又称皮尔逊积矩相关系数（Pearson product-moment correlation coefficient，简称 PPMCC或PCCs），是用于度量两个变量X和Y之间的相关（线性相关），其值介于-1与1之间。
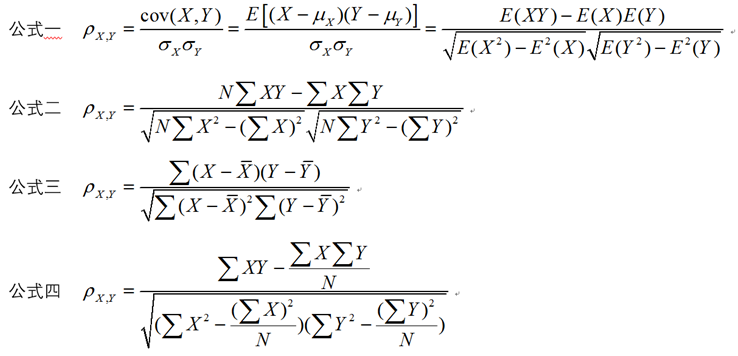
皮尔逊距离度量的是两个变量X和Y，它可以根据皮尔逊系数定义成 
我们可以发现，皮尔逊系数落在 
，而皮尔逊距离落在 
。
