并查集被很多OIer认为是最简洁而优雅的数据结构之一,主要用于解决一些元素分组的问题。它管理一系列不相交的集合,并支持两种操作:
- 合并(Union):把两个不相交的集合合并为一个集合。
- 查询(Find):查询两个元素是否在同一个集合中。
当然,这样的定义未免太过学术化,看完后恐怕不太能理解它具体有什么用。所以我们先来看看并查集最直接的一个应用场景:
我们需要知道的是,并查集最重要的操作是怎么完成的,对于属于同一组中的元素,它们存在与一个有相同根节点的树中,那么这个根节点就成为了这棵树上所有元素的代表元素,如果我们去查询两个元素是不是同一组,我们只需要返回去去找它的代表元素就可以了,如果代表元素相同就属于同一组,反之不属于;
那么我们是怎么实现这个合并的操作呢,在一开始的时候我们需要定义一个p数组用来记录每个点的父节点的是什么,然后初始化每个点为自身(这也就代表了自己就是自己这棵树的根节点);在合并时,我们只需要将这个数的代表元素的父结点指向另一个数就可以了(给自己的祖宗找了一个爹^_^);
但是我们会发现,随着这样的方式,如果这个树是一条长链,我们每次去find其根节点的时候,都需要花费不少的功夫,所以我们需要路径压缩算法,使得每个元素的父结点直接是该树的根节点(统统变成兄弟hh),这样我们的查找效率就是接近O(1)的:
int find(int x){
if(p[x] != x) p[x] = find(x); //没压缩就是 x = find(x)了
return p[x];
}
板子:
#include<bits/stdc++.h>
#define maxn 100010
using namespace std;
int pre[maxn];
int find(int x){ //这里除了查找还有路径优化操作
if(pre[x] != x) pre[x] = find(pre[x]);
return pre[x];
}
int main()
{
std::ios::sync_with_stdio(false) ; std::cin.tie(0);
int n,m;
cin>>n>>m;
for(int i = 1;i<=n;i++) pre[i] = i;
while(m--){
char order;
int a,b;
cin>>order>>a>>b;
if(order == 'M') pre[find(a)] = find(b);
else {
if(find(a) == find(b)) cout<<"Yes"<<'\n';
else cout<<"No"<<'\n';
}
}
return 0;
}
变式:如果还需要让我们求出当前这个树中所有的元素有多少个,我们只需要定义一个同样大小的cnt数组,初始化为一,代表的是以当前这个下标为根节点的树的元素数量,在每次合并时,只需要将cnt[b] += cnt[a],令新的直接加上旧的那棵树的元素大小即可!
变式:有些分组题目,我们要记录不同组之间的一个关系,而且这个组的根节点还一直在变的时候,就需要考虑一下带权值的并查集了,我们可以用带权值的关系可以通过循环来表示不同的关系,比较经典的是这道NOI的题目:
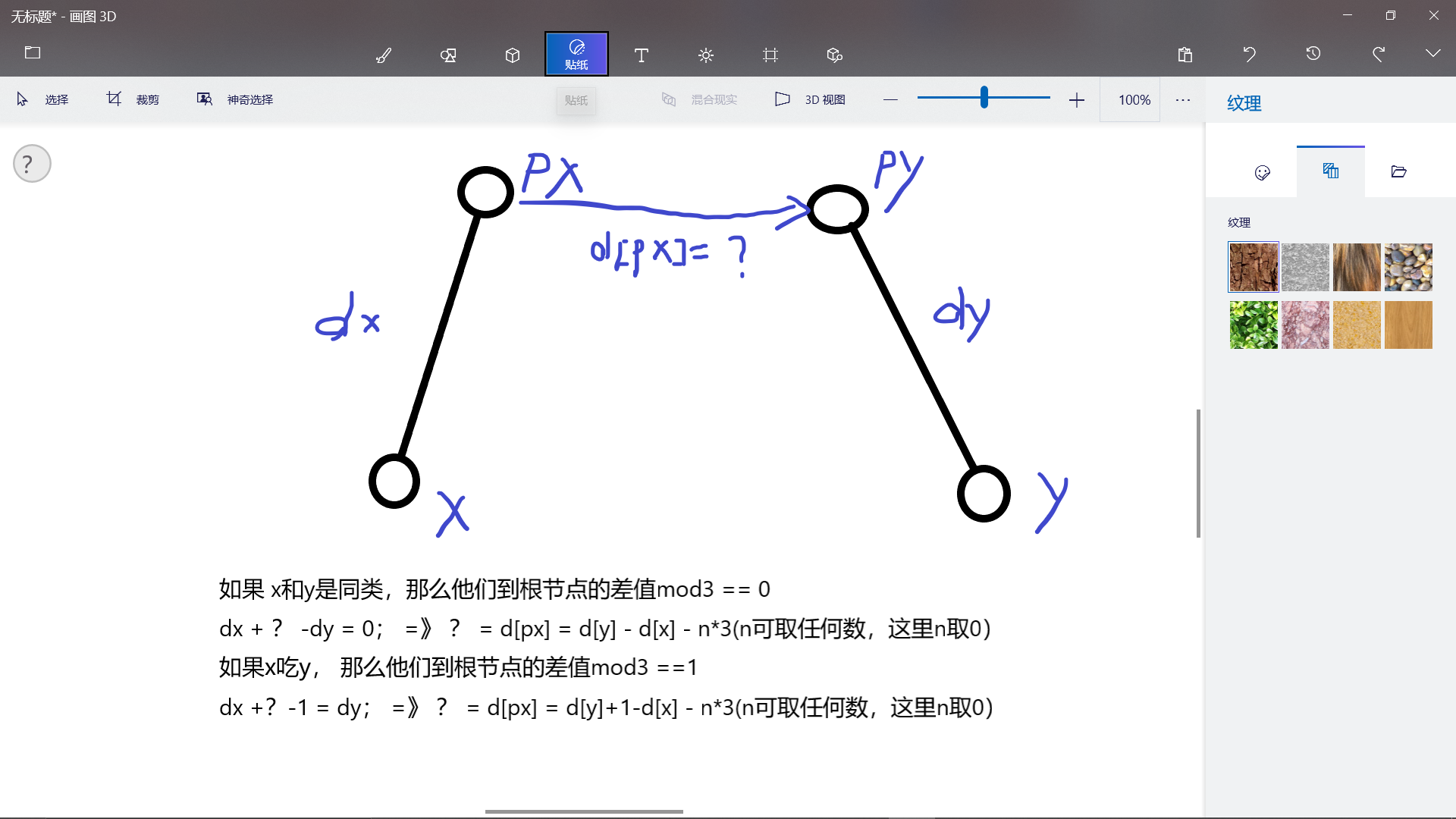
我们在这里为了要进行合并分组,用到并查集,为了要保存谁吃谁的关系,我们就要用到带权值的边,我们设置d数组,表示这个点与其父结点之间的距离,我们这里的并查集比较特殊,我们最后不是要把输入的数据区分到不同的集合,而是把他们全部放到一起去,但是用权值来表述关系,如果差mod3是0,说明是同类,如果mod3是1,说明被父亲吃,如果mod3是2,说明吃了父亲(看起来比较残忍,其实不是的qwq);
我们这里用到并查集主要是看新来的两个数本身是否已经在同一个集合中了,如果在了的话,说明权值已经分配,我们可以根据权值去判断真假(进行考验),如果不在,我们就要先把他们给合并到一起,并且分配权值(已知是真)!
答案:
#include<bits/stdc++.h>
#define maxn 50010
using namespace std;
int p[maxn],d[maxn];
int find(int x){
if(p[x] != x){
int t = find(p[x]);
d[x] += d[p[x]];
p[x] = t;
}
return p[x];
}
int main()
{
int n , k;
cin>>n>>k;
for(int i = 1; i<=n;i++) p[i] = i;
int res = 0;
while(k--){
int op,x,y;
cin>>op>>x>>y;
if(x>n || y> n) res++;
else{
int px = find(x) , py = find(y);
if(op == 1)
{
if(px == py && (d[x]-d[y]) % 3 ) res++;
else if(px != py){
p[px] = py;
d[px] = d[y] - d[x];
}
}
else
{
if(px == py && (d[x] - d[y] - 1) % 3) res++;
else if(px != py){
p[px] = py;
d[px] = d[y] + 1 - d[x];
}
}
}
}
cout<<res;
return 0;
}
解释代码:关于合并我想应该不用再多讲什么了,主要这里是如何分配权值的问题;
好了,这一部分比较难,也比较灵活,我们会在之后的算法提高课刷题中去练习!


