我们将要引入一个双指针算法,我们考虑为什么要引入双指针算法呢,以及双指针算法究竟能为我们解决什么样的问题?
通常,我们会处理到有些问题需要遍历某个序列,但根据题意我们并不需要重复判断某些过程,所以我们会利用双指针算法来取代朴素算法。将时间复杂度为O(n^2)的算法优化到O(n),就是可以不需要重复遍历某些元素。
举个栗子:
我们已知一个序列arr,我们要求出最长无重复数字的连续子串,我们用i指向右边的终点,j指向左边的起点,我们的问题是当i指向当前数字时,j最远能走到哪个位置,而当i指针往右走过去时,j指针只能向右走,不可能向左走,不然的话就向两端扩大了序列,一定会产生重复子串,这就是O(n)的算法,比起双重遍历去最值的好了太多!
如图:
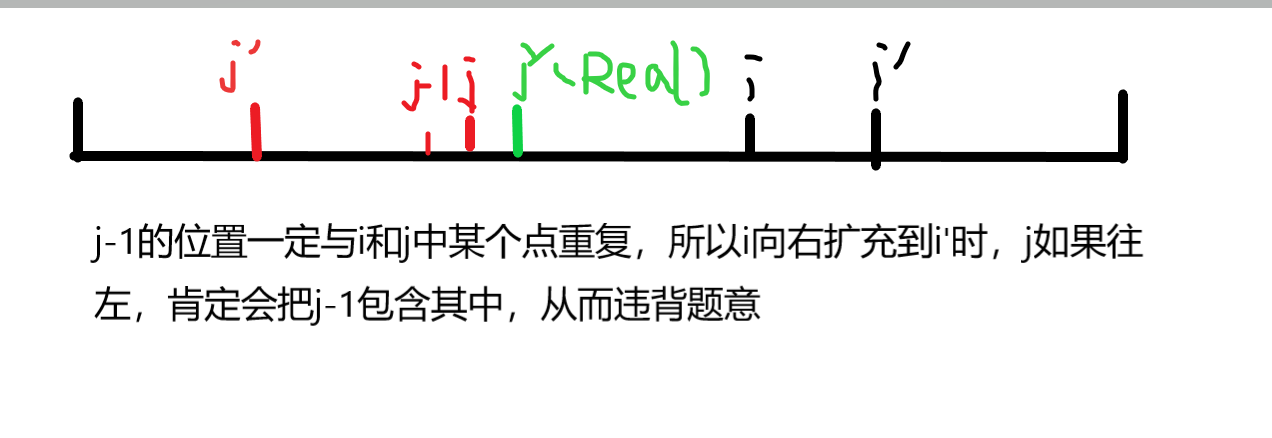
这样我们就可以知道,双指针是一个怎样的优秀算法,但是呢,我们总要先抽取出一些双指针算法的核心:
我们在遍历i的时候,只要j在范围区间之内,以及j满足某些check的条件的话,我们就可以让j++或者j--;
然后我们要大概分个几类双指针的具体算法:
·快慢指针:
·对撞指针:
某个序列我们分别让i指针从头开始,某个序列从尾开始,然后满足某种条件时停下或者完成某些操作;
举两个栗子:
· 快速排序的时候我们会定义一个x,令i指针左边都比x小,j指针右边都比x大,当arr[i]>=x 把i指针停下,当arr[j]<=x 把j指针停下,然后互换两个指针所指向的值,然后递归处理子问题,边界条件是i<=j。
·编写一个函数,以字符串作为输入,反转该字符串中的元音字母。
这个也是对撞指针,和上面差不多,只是停下指针的条件变成了遇到元音字母;然后swap两者。
·滑动窗口:
有左右端点和长度,根据题目调整左右端点的位置进行滑动,也是一种特殊的双指针
栗子:上面的最长无重复字符子串;
有些时候不仅仅是一维数组的滑动窗口,还是二维窗口的滑动窗口
板子:
#include<bits/stdc++.h>
#define maxn 100010
using namespace std;
int n;
int a[maxn],s[maxn];
int main()
{
cin>>n;
for(int i=1;i<=n;i++) scanf("%d",&a[i]);
int res = 0;
for(int i=1,j=1;i<=n;i++){
s[a[i]]++;
while(s[a[i]]>1){
s[a[j]]--;
j++;
}
res = max(res,i-j+1);
}
cout<<res<<endl;
return 0;
}
双指针算法也比较特殊:
我们之后会引入一些比较有特殊性质的例题:


