在之前我们介绍了快速排序那种优美的算法,今天又要介绍一种新的排序算法,归并排序。
归并排序的核心思想其实还是分治,我们先分成若干个子问题,然后递归处理这些子问题,然后合并之即可,一下是具体的思路:
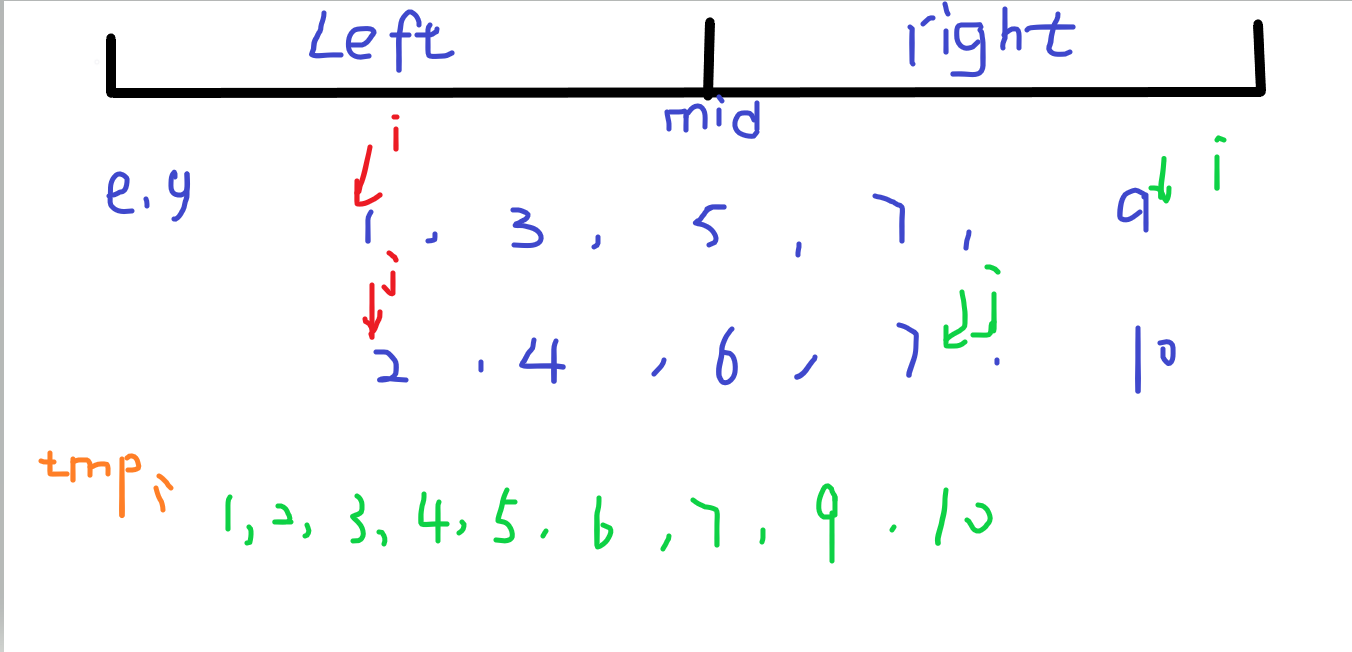
我们首先把这个序列等分为left和right,然后同样的递归处理左右两边的序列,当我们把子序列排序好之后,我们再合并成一个完整序列,这样就能完成整体序列的排序;
这个问题的难处在于把left 和right已经排序好的子序列合并起来,我们这里还是运用两个指针,都始于左侧,然后一个个地进行比较,并把较小的数给存入tmp数组中,当left或right中任一指针指到最右边的时 候,就退出循环。
但是聪明的小伙伴们一定会发现这样排完序后,left和right中一定有一个子序列的数是没有放完的,所以我们再把这个字序列中的数增添到tmp末尾即可;
最后,我们还需要把tmp数组中的数复制到q数组中来,因为我们所有的比较和输入输出都是基于q数组完成的。
以下为图解:
接下来,我们上板子进行分析,这是从小到大的:
void merge_sort(int q[],int l,int r){
//递归的终止条件
if(l>=r) return ;
//step one: 分成子问题
int mid=l+r>>1;
// step two: 递归处理子问题
merge_sort(q,l,mid);
merge_sort(q,mid+1,r);
int i=l,j=mid+1;
int k=0;
//合并子问题
while(i<=mid && j<=r){
if(q[i]<=q[j]) tmp[k++]=q[i++];
else tmp[k++]=q[j++];
}
while(i<=mid) tmp[k++]=q[i++];
while(j<=r) tmp[k++]=q[j++];
for(int i=l,j=0;i<=r;i++,j++) q[i]=tmp[j];
}
然后是从大到小的:
void merge_sort(int q[],int l,int r){
//递归的终止条件
if(l>=r) return ;
//step one: 分成子问题
int mid=l+r>>1;
// step two: 递归处理子问题
merge_sort(q,l,mid);
merge_sort(q,mid+1,r);
int i=l,j=mid+1;
int k=0;
//合并子问题
while(i<=mid && j<=r){
if(q[i]>=q[j]) tmp[k++]=q[i++];
else tmp[k++]=q[j++];
}
while(i<=mid) tmp[k++]=q[i++];
while(j<=r) tmp[k++]=q[j++];
for(int i=l,j=0;i<=r;i++,j++) q[i]=tmp[j];
}
边界分析:
边界分析
为什么不用 mid - 1 作为分隔线呢
即 merge_sort(q, l, mid - 1 ), merge_sort(q, mid, r)
因为 mid = l + r >> 1 是向下取整,mid 有可能取到 l (数组只有两个数时),造成无限划分
解决办法: mid 向上取整就可以了, 即 mid = l + r + 1 >> 1,如下所示:
void merge_sort(int q[], int l, int r)
{
if(l >= r) return;
int mid = l + r + 1>> 1;//注意mid是向上取整
merge_sort(q, l, mid - 1 ), merge_sort(q, mid, r);
int k = 0, i = l, j = mid, tmp[r - l + 1];
while(i < mid && j <= r)
if(q[i] <= q[j]) tmp[k++] = q[i++];
else tmp[k++] = q[j++];
while(i < mid) tmp[k++] = q[i++];
while(j <= r) tmp[k++] = q[j++];
for(k = 0, i = l; i <= r; k++, i++) q[i] = tmp[k];
}
不过最好不要这样写,很奇葩,不对称
为什么 用 mid 作为分隔线时不会造成无限划分呢
因为此时 mid 是向下取整的, merge_sort(q, l, mid ) 中的 mid 一定不会取到 r 值
∴ merge_sort(q, l, mid ) 不会无限划分
作者:醉生梦死
链接:https://www.acwing.com/solution/content/16778/
来源:AcWing
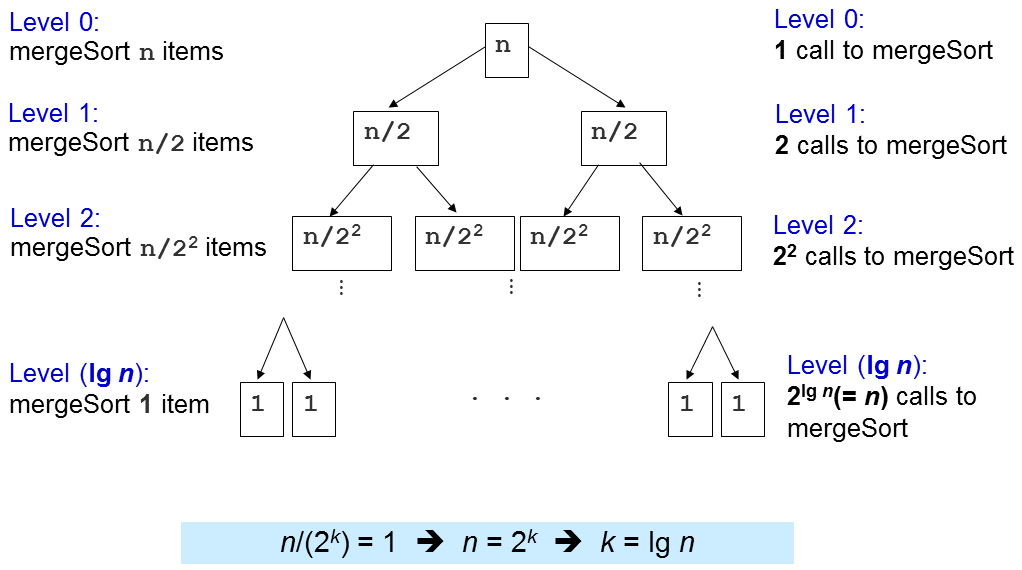
我们可以看出在递归的时候时logn,然后n个数都要遍历一遍,所以时间复杂度是O(nlogn)的
图解链接:排序(冒泡排序, 选择排序, 插入排序, 归并排序, 快速排序, 计数排序, 基数排序) - VisuAlgo
然后有这么一道例题,我们来看看怎么运用归并排序来处理它:
给定一个长度为 nn 的整数数列,请你计算数列中的逆序对的数量。
逆序对的定义如下:对于数列的第 ii 个和第 jj 个元素,如果满足 i<ji<j 且 a[i]>a[j]a[i]>a[j],则其为一个逆序对;否则不是。
输入格式
第一行包含整数 nn,表示数列的长度。
第二行包含 nn 个整数,表示整个数列。
输出格式
输出一个整数,表示逆序对的个数。
题解:我们只需要在归并排序的基础之上做一些修改就可以把这道题做出来,由于是求逆序对的个数,我们假设在left和right的序列中我们本身已经排序完成,且已经求了分别的逆序对个数,然后我们合并它,如果q[i]<=q[j]没有问题,但如果q[i]>q[j]了,就说明right中这么一个数q[j]比q[i]~q[mid]的值小,位次却比他们高,所以我们令ans+=(mid-i+1)即可,这是建立在左右子序列已经排序的状态下。
然后还有一个值得注意的地方就是,ans的数据类型应当是long long ,不然的话考虑到这道题的数据范围,很容易超出范围;
MY Code:
#include<bits/stdc++.h>
#define maxn 100010
using namespace std;
int q[maxn],tmp[maxn];
long long ans=0;
void merge_sort(int q[],int l,int r){
//递归的终止条件
if(l>=r) return ;
//step one: 分成子问题
int mid=l+r>>1;
// step two: 递归处理子问题
merge_sort(q,l,mid);
merge_sort(q,mid+1,r);
int i=l,j=mid+1;
int k=0;
//合并子问题
while(i<=mid && j<=r){
if(q[i]<=q[j]) tmp[k++]=q[i++];
else {
ans=ans+mid-i+1;
tmp[k++]=q[j++];
}
}
while(i<=mid) tmp[k++]=q[i++];
while(j<=r) tmp[k++]=q[j++];
for(int i=l,j=0;i<=r;i++,j++) q[i]=tmp[j];
}
int main()
{
int n;
cin>>n;
for(int i=0;i<n;i++) scanf("%d",&q[i]);
merge_sort(q,0,n-1);
cout<<ans;
return 0;
}
总之呢,归并排序不仅仅是可以排序这么简单,我们可以在排序的过程中做一些额外的操作,可以得到一些大小关系上的数据。


