模2运算

• 概述
• 模2加
• 模2减
• 模2乘
• 模2除

 一、概述

首先来了解什么是模2运算，模2运算与四则运算一样包括模2加、模2减、模2乘、模2除四种二进制运算，与四则运算不同的是模2运算不考虑进位和错位，模2运算是编码理论中多项式运算的基础。

移位寄存器的每一级只可能有两种不同的存数(或状态)，分别用0和1来表示。这里，0和1不再具有一般数量的含义，而只具有逻辑含义。对于这样一种只包含0和1两个元素(符号)的集合(较做二元集)来说，普通的四则运算不再适用，因而必须重新规定一种新的运算规则。

模2运算也是用与四则运算相同的运算规符，即“+”表示模2加，“-”表示模2减，“x”或“·”表示模2乘，“÷”或“/”表示模2除。与四则运算不同的是模2运算不考虑进位和错位，即模2加法是不带进位的二进制加法运算，模2减法是不带错位的二进制减法运算。这样，两个二进制位相运算时，这两个位的值就能确定运算结果，不受前一次运算的影响，也不对下一次造成影响。

 二、模2加法

所谓“模2加法”就是0和1之间的加法，其中0+0=0，1+0=0+1=1，1+1=0(!)。这种运算在通信和计算机上是常用的，而且并不神秘，你可以把0和1分别想成“偶数”和“奇数”，那么前两个式子分别代表：偶数加偶数等于偶数，奇数加奇数等于奇数，而式1+1=0就是奇数加奇数等于偶数。对于任意多个a1，a2，...，am（每个都是0或1），可以把他们做2加法a1+a2+...，+am，当这m个数中有奇数个1时，结果为1，否则结果为0。

对于二进制数定义模2加法，规则非常简单：即每个数位上分别做模2加法，由此得出一个新的二进制数，例如[1101]+[111]+[101]=[1111]，写成算式为：

上面的算式的解释：个位共有3个1，所以模2加为1(不进位)。同样的，其他数位上也均有奇数个1，不同数位之间彼此无关地运算，所以上面的算式结果为[1111]。

 三、模2减法

所谓模2减法就是不考虑借位的减法，其中0-0=0，1-1=0，1-0=1，0-1=1，最后一个式子0-1代表模2减法的特征，从它也可以得出2=0及+1=-1的结论，在多位模减法中，每位都按上述定义进行运算，不考虑借位问题。比如下面这个式子：

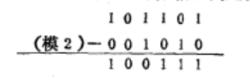
从上面这个式子中可以发现模2加法和减法的结果完全一样，这是模2加法和减法一个重要的特征，所以用模2减法的地方都可以用模2加法替代，故而模2减法不用定义专用的符号。

模2加的定义可以得出一个结论：奇数个1相加得1，偶数个1相加得0，这个结论在奇偶校验中非常有用。

 四、模2乘法

 一位数得模2乘法定义如下：0x0=0，0x1=0，1x0=0，1x1=1，下面是一个多位数得模2乘法得式子示例：

 

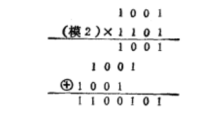
模2乘法与普通四则运算差不多，唯一得差别就是乘积部分按照模2加法计算，在上面得示例中1101用四则运算得说法来说就是个百千位有有效乘积，即乘数个百千位为1，所以它们得乘积得最低位都跟着它们得乘积位一致这与四则运算是一样，不一样得就是它们得乘积使用模2加计算得出最后得多位数模2乘法结果。

 五、模2除法

模2除法是模2乘法得逆运算，如下面得示例：

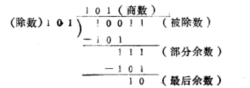
模2除法具有下列三个性质：

当最后余数得位数小于除数位数时，除法停止；

当被除数得位数小于除数位数时，则商数为0，被除数就是余数；

只要被除数或部分余数得位数与除数一样多，且最高位为1，不管其他位是什么数，皆可商1；

前面这个示例来源百度，可能第一次看起来不是很理解，可以用前面模2乘法得式子来做一个逆运算：

每一步得计算就是用除数与余数位做模2减法，虽然模2减法与结果是一样的，但最好按照乘法的逆运算逻辑来理解，然后再仔细观察会发现模2运算中的加减法也是异或运算，有的相关内容解析中也会用异或运算来解释模2运算：0表示假，1表示真，0与1做或运算，即假假为假、真假为真、假真为真，实际上异或运算的本质就是模2运算的加减运算。