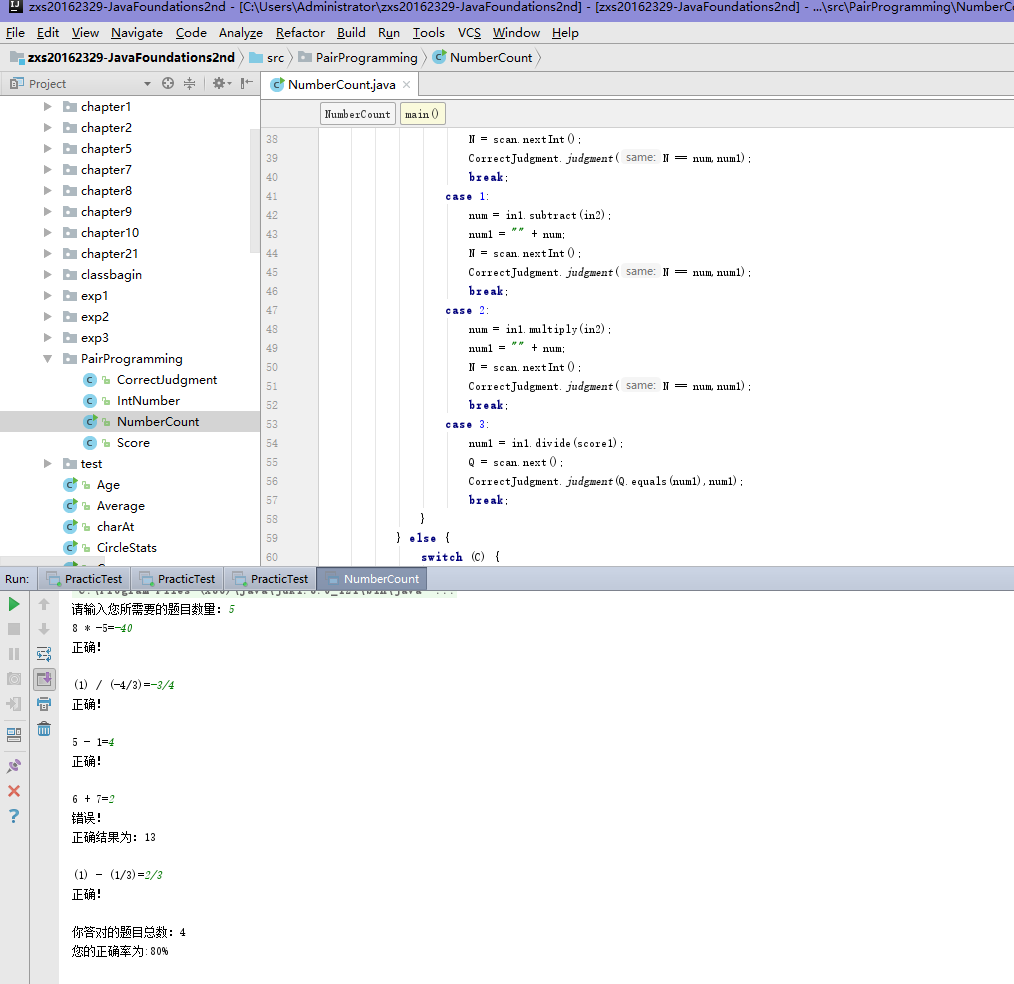
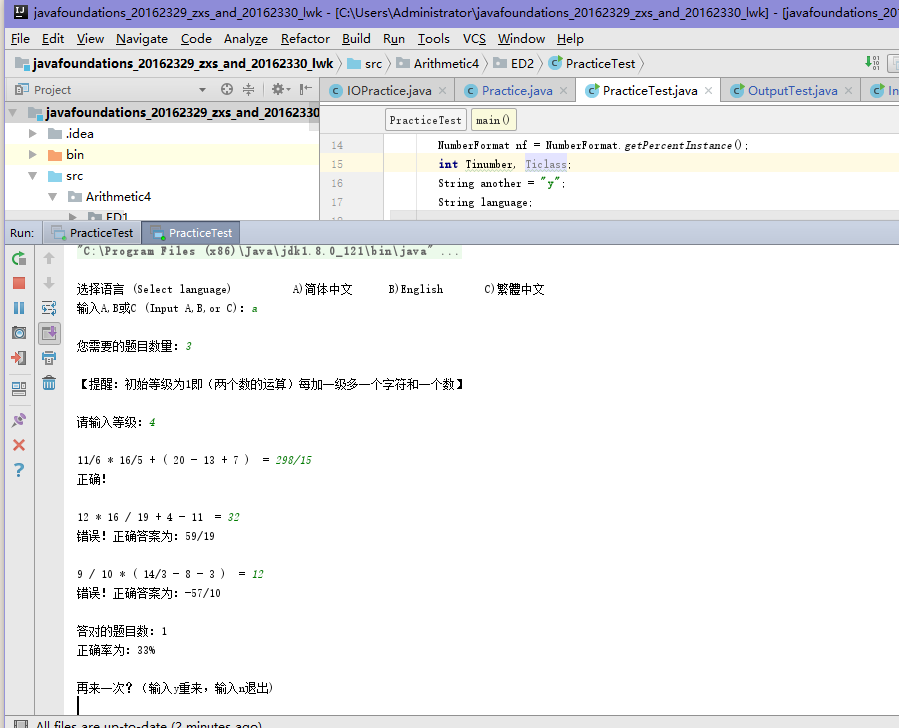
四则运算的整体总结(第二周)
四则运算整体总结
结对对象
学号 :20162330
姓名 : 刘伟康
UML
不用栈的方法:
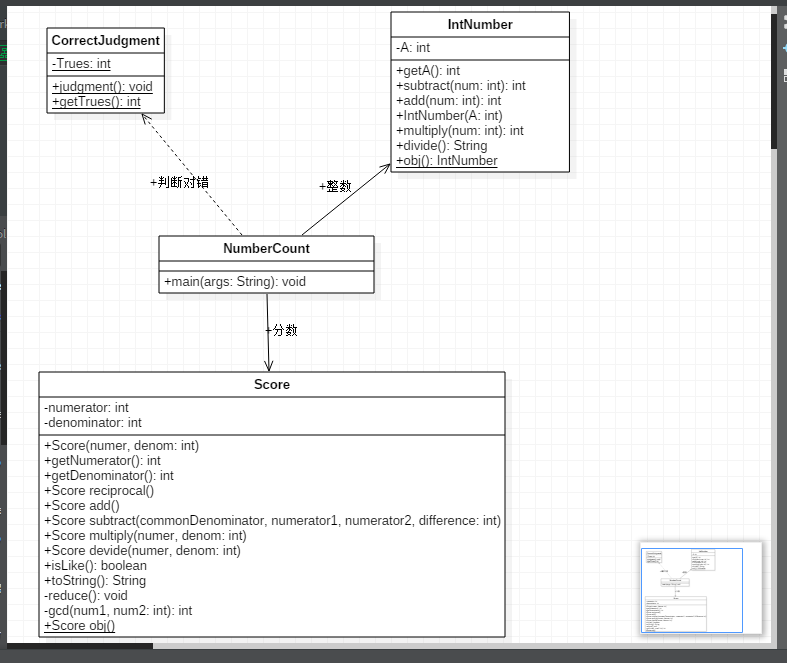
用栈的方法:
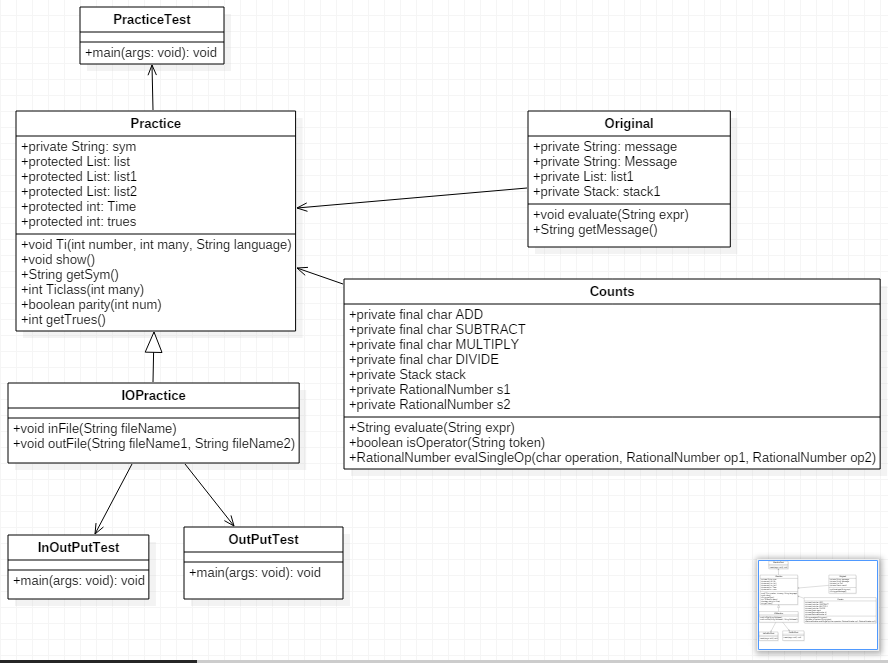
一、需求分析
-
需要一个整数计算类
-
需要一个分数计算类
-
需要一个可自动生成题目的类
-
需要一个测试结果的类
扩展需求
-
需要一个IO输出流对自动生成的题目写入文件
-
需要一个IO输入流读入文件内容并判断正误
-
需要一个去除生成题目中重复出现的题目的方法
综上有两种办法:
-
用栈的方法计算(本周主要研究的内容)
-
不用栈的方法计算(上周博客以明确给出)
二、设计思路
方法一(不用栈的方法):
优点:
-
思路简单,易实现。
-
主要需求bug少
缺点:
-
扩展需求难于实现
-
不支持复杂计算
方法二(用栈的方法)“本周对其进行了进一步优化":
优点:
-
可进行多运算符的精确计算
-
可实现功能更多
三、关键代码解释:
中缀转后缀表达式转换类:
通过观察和了解,对于运用栈的中缀转后缀方法,以及对后缀表达式的计算类同学们大都可以自己完成所以不属于我的主要代码,通过多位同学看完我的代码所给的反馈,我在这里对我的题目自动生成以及加括号的方法进行解释:
public void Ti(int number, int many,String language) {
if(language.equalsIgnoreCase("A"))
many = TiclassC(many);
else if(language.equalsIgnoreCase("B"))
many = TiclassE(many);
else many = TiclassF(many);
for (int j = 0; j < number; j++) {
String ti = "";
//开始进入题目生成
for (int i = 0; i < many; i++) {
int A = ran.nextInt(20) + 1;
int D = ran.nextInt(20) + 1;
int B = ran.nextInt(5);
int C = ran.nextInt(5);
RationalNumber si = new RationalNumber(A, D);
//正式进入生成题目
if (parity(i)) {
//判断前面是否有左括号
if (list1.indexOf("( ") == -1)
list1.add(getSym() + " ");
//判断将加的右括号和上一个左括号的距离
else if (list1.size() - list1.lastIndexOf("( ") > 4) {
//判断前面的左括号是否已经有了相对应的右括号了
if (list1.lastIndexOf(") ") - list1.lastIndexOf("( ") < 0 && B == 0) {
list1.add(") ");
list1.add(getSym() + " ");
} else list1.add(getSym() + " ");
} else list1.add(getSym() + " ");
} else if (i == many - 1) {
//循环结束时判断前面是否还有一个没有加右括号的左括号
if (list1.lastIndexOf("( ") - list1.lastIndexOf(") ") > 0) {
if (C == 0) {
list1.add(si.toString() + " ");
list1.add(") ");
} else {
list1.add(A + " ");
list1.add(") ");
}
} else if (C != 0)
list1.add(A + " ");
else list1.add(si.toString() + " ");
} else if (i == 0) {
if (C != 0)
list1.add(A + " ");
else list1.add(si.toString() + " ");
} else if (list1.lastIndexOf(") ") != -1) {
if (list1.lastIndexOf(") ") - list1.lastIndexOf("( ") > 0 && B == 0) {
list1.add("( ");
if (C != 0)
list1.add(A + " ");
else list1.add(si.toString() + " ");
} else if (C != 0)
list1.add(A + " ");
else list1.add(si.toString() + " ");
} else if (list1.indexOf("( ") == -1 && B == 0) {
list1.add("( ");
if (C != 0)
list1.add(A + " ");
else list1.add(si.toString() + " ");
} else if (C != 0)
list1.add(A + " ");
else list1.add(si.toString() + " ");
}
for (String i : list1)
ti += i;
list1.clear();
list.add(ti);
}
}
public String getSym() {
int A = ran.nextInt(4);
switch (A) {
case 0:
sym = "+";
break;
case 1:
sym = "-";
break;
case 2:
sym = "*";
break;
case 3:
sym = "/";
break;
}
return sym;
}
public boolean parity(int num) {
if (num % 2 == 1)
return true;
else
return false;
}
public int TiclassC(int many) {
Scanner scan = new Scanner(System.in);
int A = 1;
while (true) {
try {
if (many > 0) {
for (int i = 0; i < many; i++) {
A += 2;
}
break;
} else throw new Exception();
}
catch (Exception e) {
System.out.println("级别输入错误,请重新输入(要求级别至少为1)");
many = scan.nextInt();
}
}
return A;
}
以上是相关代码:
-
解释:首先在用户输入题目数量
number和题目等级many后many会在Ticlass方法中转换为相应等级的长度,根据输入的两个参数建立两个循环,具体思路为:生成的题目都是在双数位为数字,但数位为符号,在此基础上,在加数字时可能会在数字的左边加一个“(”,在加符号时会在符号的左边加一个“)”,但在加“)”时需要进行判断1.前面是否存在一个“(” 2.前面的“(”后面是否已经有了“)” 3.前的“(”距离现在要加的“)”是否存在一定距离(以此保证括号中至少扩入一个两个数的计算)为解决这个问题,我使用了ArrayList中的Indexof和lastIndexof方法我将每一个生成的符号或数字都顺序加入到list中用最后一个“)”位置与最后一个“(”位置做差后所的数的大小来判断和保证括号生成都是一对的。



四、结对评价
上周我基本就已经将所有需要的主要类都完成,这周我只是在类中加了一个可以将生成题目写入文件然后用户在文件中回答完毕后再读入判断正误计算正确率再返回文件的类。这周主要修改都是刘伟康同学进行的,他在深入看完我写的代码后理解了大部分,代码然后对用户类的一些bug进行了修复,比如再用户输入了错误的题目数量或是等级时会弹出提示然后让用户重新输入,刘伟康还给代码加入了多语言的选择,刘伟康同学虽然学的慢但是好在很有耐心,也很爱探索,这次的合作我们很成功。
五、遇到的问题及解决方法
问题:在题目生成过程中只能生成符带有号和数字的表达式却不能生成带有括号的混合运算。
解决办法:在查过文档后,我发现了一个列表(List)的很好用的方法,IndexOf(object o)和lastIndexOf(object o)分别是返回列表中首次出现某个对象的位置和最后一次出现某个对象的位置,利用左右括号的位置差进行判断,最终实现加多个括号的表达式生成。
六、压力测试
我为我的题目生成设置了生成等级,即 两个数字一个符号为一级,每加一级符号和数字个加一个,以此类推,然后我利用这个功能进行了多符号表达式的生成的压力测试:
- 等级10:0.5秒以下;
- 等级100:1秒以下;
- 等级1000:1秒以下;
- 等级10000: 3秒左右;
- 等级100000: 4分钟左右;
PSP
| PSP2.1 | Personal Software Process Stages | 预估耗时(小时) | 实际耗时(小时) |
|---|---|---|---|
| Planning | 计划 | 1 | 1 |
| · Estimate | · 估计这个任务需要多少时间 | 20 | 20 |
| · Analysis | · 需求分析 (包括学习新技术) | 1 | 3 |
| · Design Spec | · 生成设计文档 | 0.5 | 0.5 |
| · Design Review | · 设计复审 (和同事审核设计文档) | 1 | 0.5 |
| · Coding Standard | · 代码规范 (为目前的开发制定合适的规范) | 1 | 0.5 |
| · Design | · 具体设计 | 2 | 3 |
| · Coding | · 具体编码 | 2 | 4 |
| · Code Review | · 代码复审 | 2 | 1 |
| · Test | · 测试(自我测试,修改代码,提交修改) | 2 | 1 |
| ·Reporting | ·报告 | 1 | 1.5 |
| · Test Report | · 测试报告 | 2 | 2.5 |
| · Size Measurement | · 计算工作量 | 0.5 | 0.5 |
| · Postmortem & Process Improvement Plan | · 事后总结, 并提出过程改进计划 | 1 | 1 |