详解RSA加密原理
密码学
-
密码学是指研究信息加密,破解密码的技术科学。密码学的起源可追溯到2000年前。而当今的密码学是以数学为基础的。
-
密码学的历史大致可以追溯到两千年前,相传古罗马名将凯撒大帝为了防止敌方截获情报,用密码传送情报。凯撒的做法很简单,就是对二十几个罗马字母建立一张对应表。这样,如果不知道密码本,即使截获一段信息也看不懂。 从凯撒大帝时代到上世纪70年代这段很长的时间里,密码学的发展非常的缓慢,因为设计者基本上靠经验。没有运用数学原理
发展历史
- 在1976年以前,所有的加密方法都是同一种模式:加密、解密使用同一种算法。在交互数据的时候,彼此通信的双方就必须将规则告诉对方,否则没法解密。那么加密和解密的规则(简称密钥),它保护就显得尤其重要。传递密钥就成为了最大的隐患。这种加密方式被成为对称加密算法(symmetric encryption algorithm) 1976年,两位美国计算机学家 迪菲(W.Diffie)、赫尔曼( M.Hellman ) 提出了一种崭新构思,可以在不直接传递密钥的情况下,完成密钥交换。这被称为“迪菲赫尔曼密钥交换”算法。开创了密码学研究的新方向
- 1977年三位麻省理工学院的数学家 罗纳德·李维斯特(Ron Rivest)、阿迪·萨莫尔(Adi Shamir)和伦纳德·阿德曼(Leonard Adleman)一起设计了一种算法,可以实现非对称加密。这个算法用他们三个人的名字命名,叫做RSA算法。
RSA数学原理
-
上世纪70年代产生的一种加密算法。其加密方式比较特殊,需要两个密钥:公开密钥简称公钥(publickey)和私有密钥简称私钥(privatekey)。公钥加密,私钥解密;私钥加密,公钥解密。这个加密算法就是伟大的RSA
欧拉函数φ :任意给定正整数n,请问在小于等于n的正整数之中,有多少个与n构成互质关系?
- 互质关系:如果两个正整数,除了1以外,没有其他公因数,我们就称这两个数是互质关系(coprime)
计算这个值的方式叫做欧拉函数,使用:中(n)表示
如:
计算8的欧拉函数,和8互质的1、2、3、4、5、6、7、8
φ(8) = 4
计算7的欧拉函数,和7互质的1、2、3、4、5、6、7
ф(7)=6
计算56的欧拉函数
ф(56) = ф(8) * φ(7) = 4 * 6 = 24
- 欧拉函数特点
当n是质数的时候,@(n)=n-1。
如果n可以分解成两个互质的整数之积,如
n=A*B则:
ф(A*B)=ф(A)* ф(B)
根据以上两点得到:
如果N是两个质数P1和P2的乘积则
ф(N)=ф(P1)* (P2)=(P1-1)*(P2-1)
欧拉定理
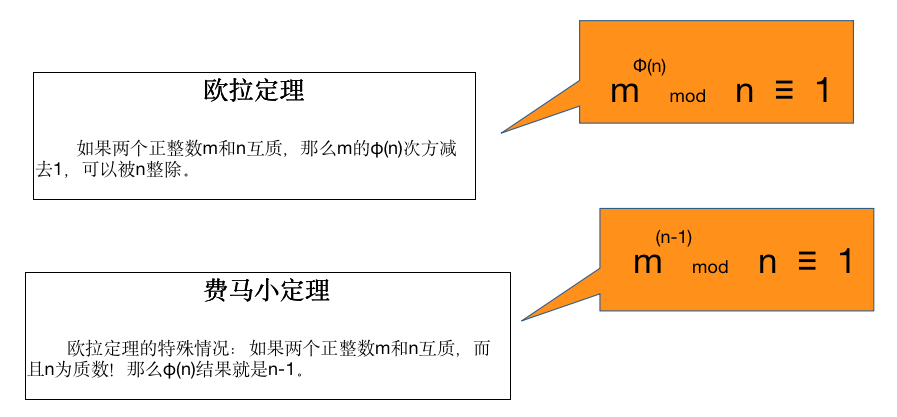
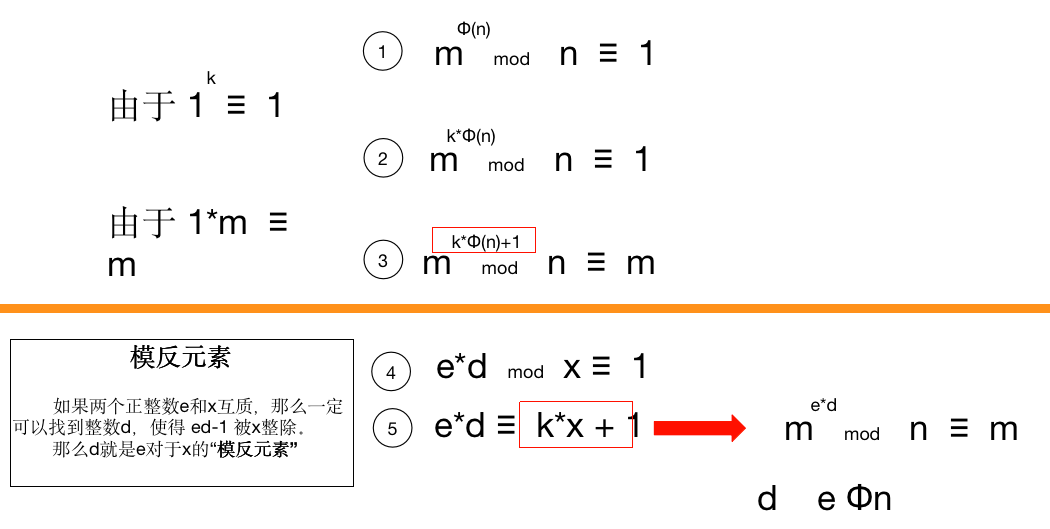
模反元素
迪菲赫尔曼密钥交换
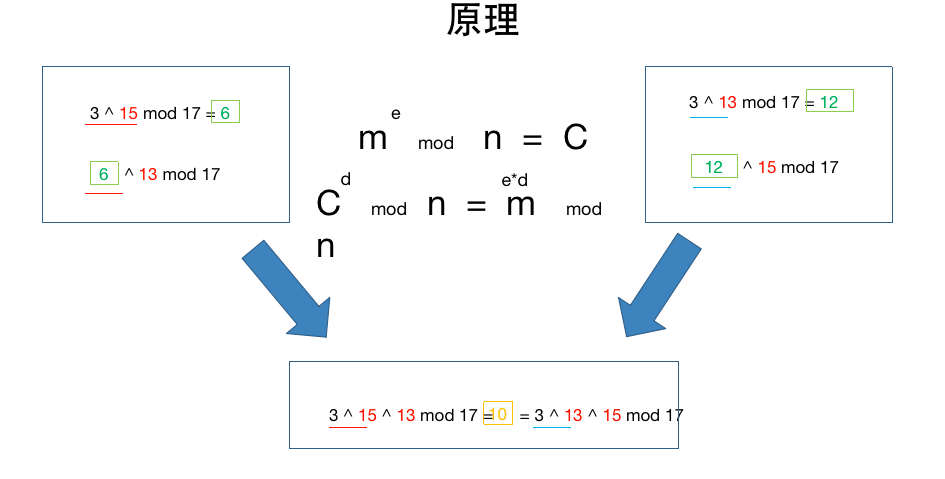
RSA的诞生
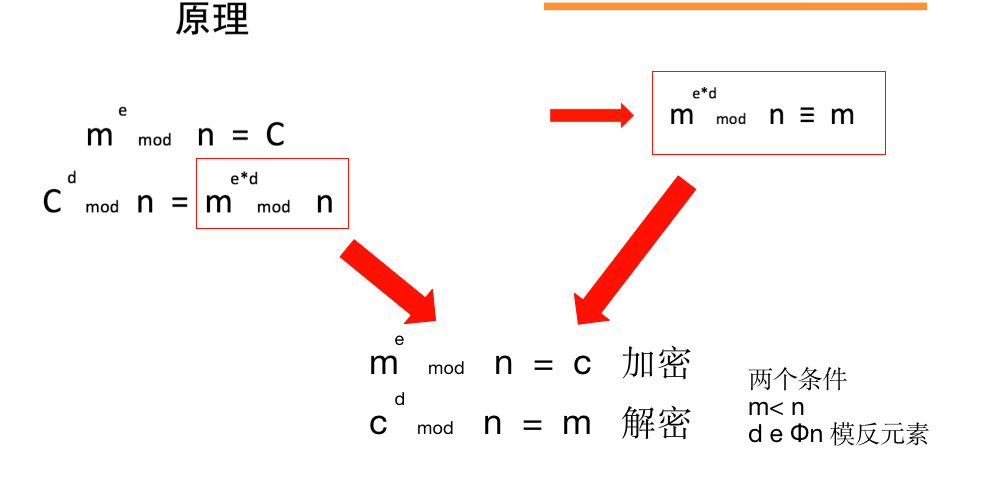
RSA算法






【推荐】国内首个AI IDE,深度理解中文开发场景,立即下载体验Trae
【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· TypeScript + Deepseek 打造卜卦网站:技术与玄学的结合
· 阿里巴巴 QwQ-32B真的超越了 DeepSeek R-1吗?
· 【译】Visual Studio 中新的强大生产力特性
· 10年+ .NET Coder 心语 ── 封装的思维:从隐藏、稳定开始理解其本质意义
· 【设计模式】告别冗长if-else语句:使用策略模式优化代码结构