二叉树和B树详解

1、树（Tree）的基本概念

 

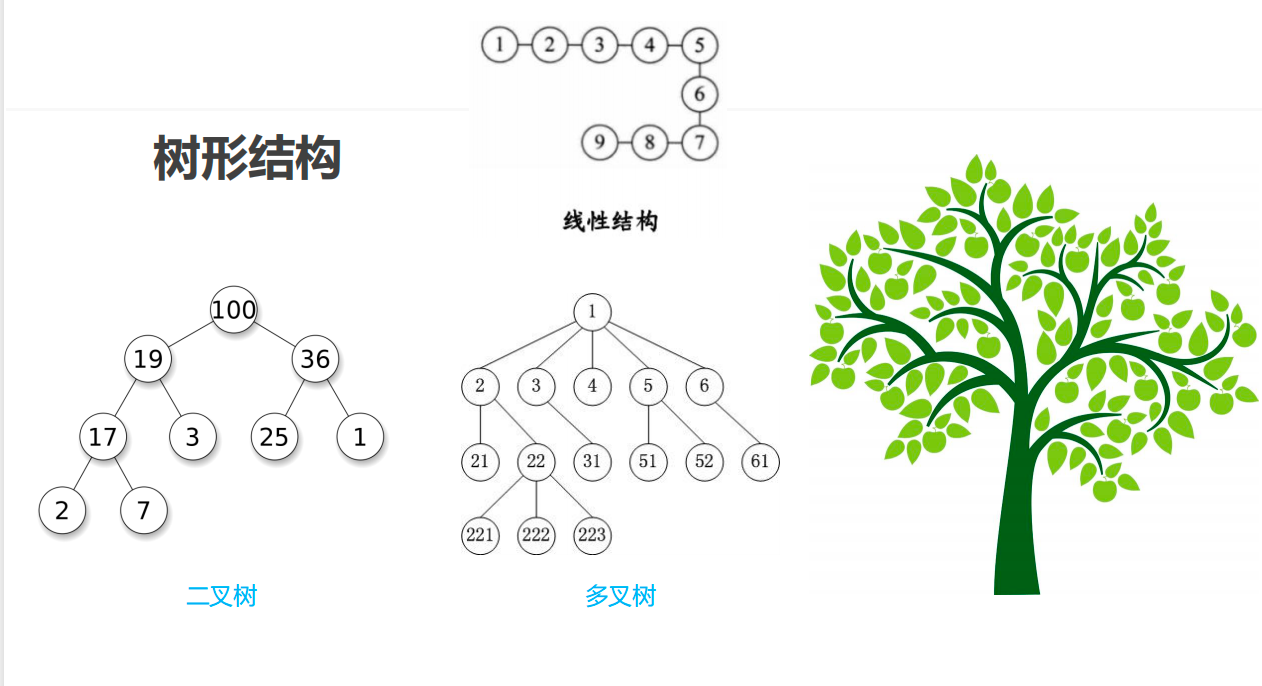
1. 节点、根节点、父节点、子节点、兄弟节点
2. 一棵树可以没有任何节点，称为空树
3. 一棵树可以只有 1 个节点，也就是只有根节点
4. 子树、左子树、右子树
5. 节点的度（degree）：子树的个数
6. 树的度：所有节点度中的最大值
7. 叶子节点（leaf）：度为 0 的节点
8. 非叶子节点：度不为 0 的节点
9. 层数（level）：根节点在第 1 层，根节点的子节点在第 2 层，以此类推（有些教程也从第 0 层开始计算）
10. 节点的深度（depth）：从根节点到当前节点的唯一路径上的节点总数
11. 节点的高度（height）：从当前节点到最远叶子节点的路径上的节点总数
12. 树的深度：所有节点深度中的最大值
13. 树的高度：所有节点高度中的最大值
14. 树的深度 等于 树的高度

2、有序树、无序树、森林

 

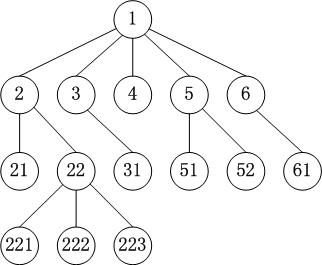
◼ 有序树

树中任意节点的子节点之间有顺序关系

◼ 无序树

树中任意节点的子节点之间没有顺序关系

也称为“自由树”

◼ 森林

由 m（m ≥ 0）棵互不相交的树组成的集合

3、二叉树（Binary Tree）

 

二叉树的特点

1. 每个节点的度最大为 2（最多拥有 2 棵子树）
2. 左子树和右子树是有顺序的
3. 即使某节点只有一棵子树，也要区分左右子树

二叉树是有序树 还是 无序树？

有序树

二叉树的性质

• 非空二叉树的第 i 层，最多有 2^ (i − 1) 个节点（ i ≥ 1 ）
• 在高度为 h 的二叉树上最多有 2^ h − 1 个结点（ h ≥ 1 ）
• 对于任何一棵非空二叉树，如果叶子节点个数为 n0，度为 2 的节点个数为 n2，则有: n0 = n2 + 1
• 假设度为 1 的节点个数为 n1，那么二叉树的节点总数 n = n0 + n1 + n2
• 二叉树的边数 T = n1 + 2 * n2 = n – 1 = n0 + n1 + n2 – 1
• 因此 n0 = n2 + 1

真二叉树（Proper Binary Tree）

真二叉树：所有节点的度都要么为 0，要么为2

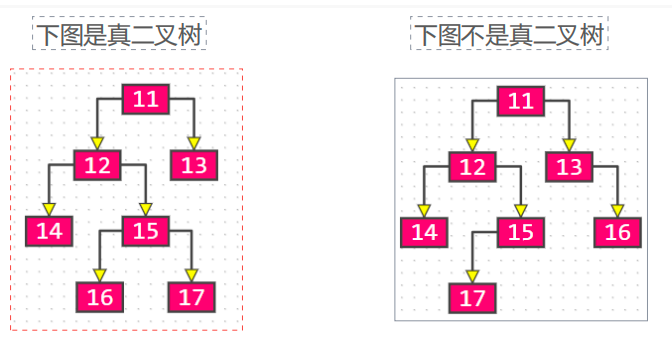
满二叉树（Full Binary Tree）

满二叉树：最后一层节点的度都为 0，其他节点的度都为 2

 

 

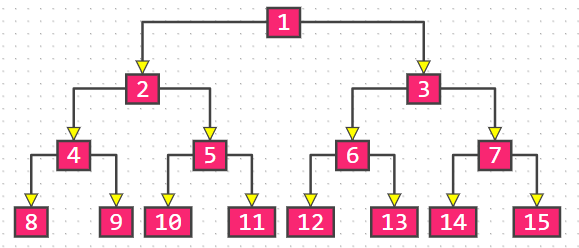
◼ 在同样高度的二叉树中，满二叉树的叶子节点数量最多、总节点数量最多

◼ 满二叉树一定是真二叉树，真二叉树不一定是满二叉树

◼ 假设满二叉树的高度为 h（ h ≥ 1 ），那么

第 i 层的节点数量： 2^( i − 1)

叶子节点数量： 2^ h − 1

总节点数量 n

✓n = 2^ h − 1 = 2^ 0 + 2^1 + 2^2 + ⋯ + 2^( h−1)

✓h = log2(n + 1)

完全二叉树（Complete Binary Tree）

完全二叉树：对节点从上至下、左至右开始编号，其所有编号都能与相同高度的满二叉树中的编号对应

 

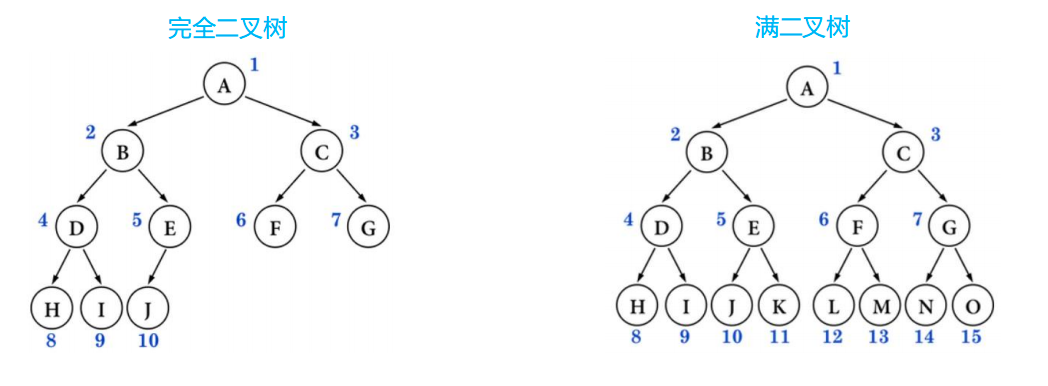
• 叶子节点只会出现最后 2 层，最后 1 层的叶子结点都靠左对齐
• 完全二叉树从根结点至倒数第 2 层是一棵满二叉树
• 满二叉树一定是完全二叉树，完全二叉树不一定是满二叉树

◼ 度为 1 的节点只有左子树

◼ 度为 1 的节点是只有1 个

◼ 同样节点数量的二叉树，完全二叉树的高度最小

◼ 假设完全二叉树的高度为 h（ h ≥ 1 ），那么

至少有 2 ^(h − 2) 个节点 （ 2^ 0 + 2^ 1 + 2^ 2 + ⋯ + 2^( h−2) + 1 ）

最多有 2^( h − 1) 个节点（ 2^ 0 + 2^ 1 + 2 ^2 + ⋯ + 2^( h−1)，满二叉树 ）

总节点数量为 n

✓ 2 ^(h − 1) ≤ n < 2^ h

✓ h − 1 ≤ log2n < h

✓ h = floor( log2n ) + 1

➢ floor 是向下取整，另外，ceiling 是向上取整

 

 

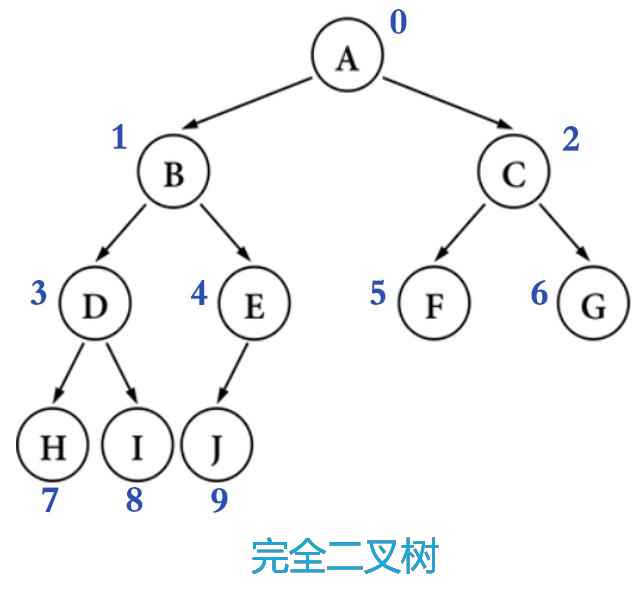
◼ 一棵有 n 个节点的完全二叉树（n > 0），从上到下、从左到右对节点从 0 开始进行编号，对任意第 i 个节点

• 如果 i = 0 ，它是根节点
• 如果 i > 0 ，它的父节点编号为 floor( (i – 1) / 2 )
• 如果 2i + 1 ≤ n – 1 ，它的左子节点编号为 2i + 1
• 如果 2i + 1 > n – 1 ，它无左子节点
• 如果 2i + 2 ≤ n – 1 ，它的右子节点编号为 2i + 2
• 如果 2i + 2 > n – 1 ，它无右子节点

 

面试题：如果一棵完全二叉树有 768 个节点，求叶子节点的个数

◼ 如果一棵完全二叉树有 768 个节点，求叶子节点的个数

• 假设叶子节点个数为 n0，度为 1 的节点个数为 n1，度为 2 的节点个数为 n2
• 总结点个数 n = n0 + n1 + n2，而且 n0 = n2 + 1

✓ n = 2n0 + n1 – 1

• 完全二叉树的 n1 要么为 0，要么为 1

✓ n1为1时，n = 2n0，n 必然是偶数

➢ 叶子节点个数 n0 = n / 2，非叶子节点个数 n1 + n2 = n / 2

✓ n1为0时，n = 2n0 – 1，n 必然是奇数

➢ 叶子节点个数 n0 = (n + 1) / 2，非叶子节点个数 n1 + n2 = (n – 1) / 2

• 叶子节点个数 n0 = floor( (n + 1) / 2 ) = ceiling( n / 2 )
• 非叶子节点个数 n1 + n2 = floor( n / 2 ) = ceiling( (n – 1) / 2 )
• 因此叶子节点个数为 384

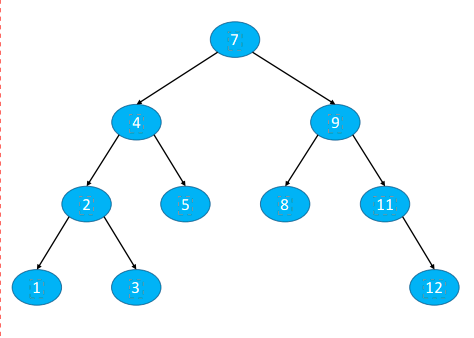
二叉搜索树（Binary Search Tree）

 

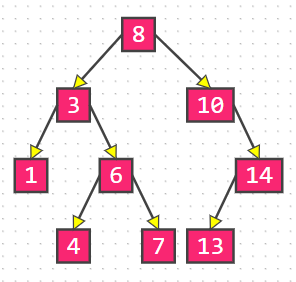
◼ 二叉搜索树是二叉树的一种，是应用非常广泛的一种二叉树，英文简称为 BST

又被称为：二叉查找树、二叉排序树

• 任意一个节点的值都大于其左子树所有节点的值
• 任意一个节点的值都小于其右子树所有节点的值
• 它的左右子树也是一棵二叉搜索树
• 二叉搜索树可以大大提高搜索数据的效率
• 二叉搜索树存储的元素必须具备可比较性
• 比如 int、double 等
• 如果是自定义类型，需要指定比较方式
• 不允许为 null

◼ 需要注意的是

对于我们现在使用的二叉树来说，它的元素没有索引的概念

添加节点

 

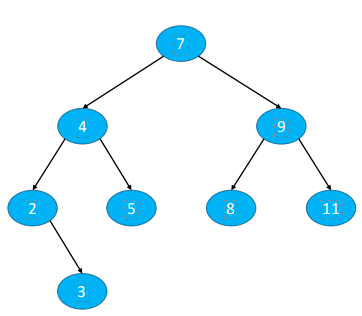
添加步骤

• 找到父节点 parent
• 创建新节点 node
• parent.left = node 或者 parent.right = node
• 遇到值相等的元素该如何处理？
• 建议覆盖旧的值

思考：添加 12、1添加在哪里?

 

 

4、B树（B-tree、B-树）

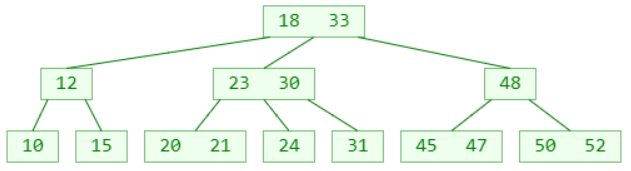
三阶B树

 

四阶B树

 

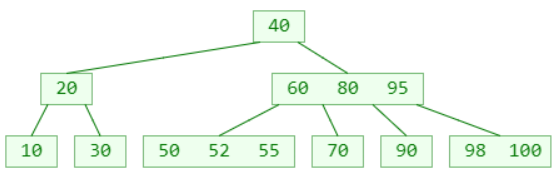
五阶B树

 

• B树是一种平衡的多路搜索树，多用于文件系统、数据库的实现
• 仔细观察B树，有什么眼前一亮的特点？
• 1 个节点可以存储超过 2 个元素、可以拥有超过 2 个子节点
• 拥有二叉搜索树的一些性质
• 平衡，每个节点的所有子树高度一致
• 比较矮

m阶B树的性质（m≥2）

 

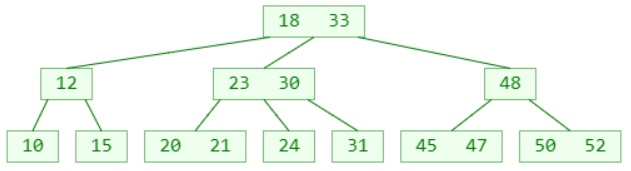
◼ 假设一个节点存储的元素个数为 x

根节点：1 ≤ x ≤ m − 1

非根节点：┌ m/2 ┐ − 1 ≤ x ≤ m − 1

如果有子节点，子节点个数 y = x + 1

✓ 根节点：2 ≤ y ≤ m

✓ 非根节点：┌ m/2 ┐ ≤ y ≤ m

➢ 比如 m = 3，2 ≤ y ≤ 3，因此可以称为（2, 3）树、2-3树

➢ 比如 m = 4，2 ≤ y ≤ 4，因此可以称为（2, 4）树、2-3-4树

➢ 比如 m = 5，3 ≤ y ≤ 5，因此可以称为（3, 5）树

➢ 比如 m = 6，3 ≤ y ≤ 6，因此可以称为（3, 6）树

➢ 比如 m = 7，4 ≤ y ≤ 7，因此可以称为（4, 7）树

◼ 思考：如果 m = 2，那B树是什么样子？

◼ 你猜数据库实现中一般用几阶B树？

200 ~ 300

B树 VS 二叉搜索树

 

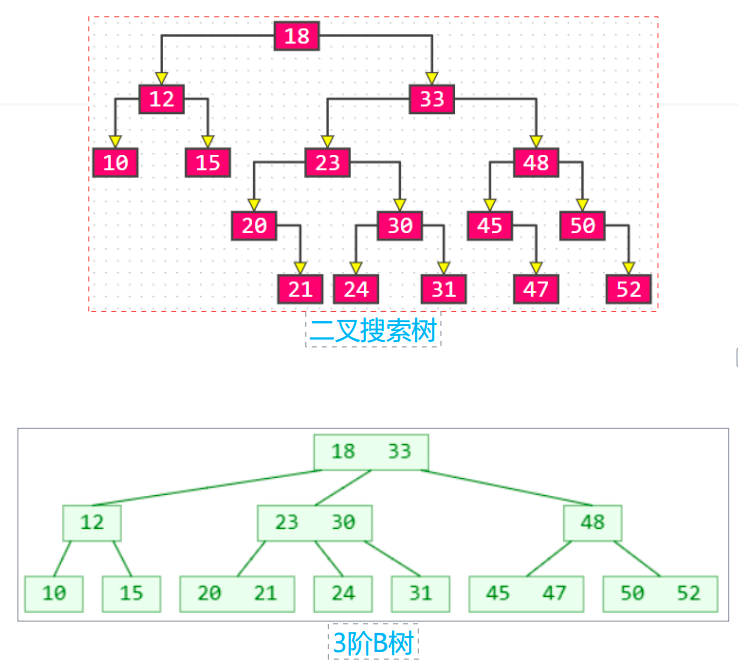
• B树 和 二叉搜索树，在逻辑上是等价的
• 多代节点合并，可以获得一个超级节点
• 2代合并的超级节点，最多拥有 4 个子节点（至少是 4阶B树）
• 3代合并的超级节点，最多拥有 8 个子节点（至少是 8阶B树）
• n代合并的超级节点，最多拥有 2 n个子节点（ 至少是 2 n阶B树）
• m阶B树，最多需要 log2m 代合并

搜索

 

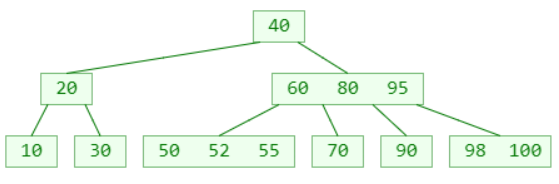
1. 先在节点内部从小到大开始搜索元素

2. 如果命中，搜索结束

3. 如果未命中，再去对应的子节点中搜索元素，重复步骤 1

添加

 

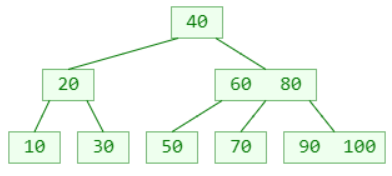
新添加的元素必定是添加到叶子节点

例：插入55

 

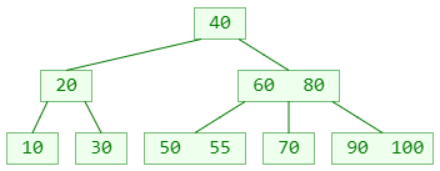
例：插入95

 

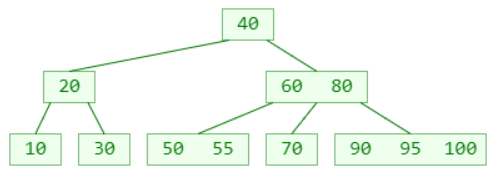
再插入 98 呢？（假设这是一棵 4阶B树）

最右下角的叶子节点的元素个数将超过限制

这种现象可以称之为：上溢（overflow）

上溢的解决(假设5阶)

◼ 上溢节点的元素个数必然等于 m

◼ 假设上溢节点最中间元素的位置为 k

将 k 位置的元素向上与父节点合并

将 [0, k-1] 和 [k + 1, m - 1] 位置的元素分裂成 2 个子节点

✓ 这 2 个子节点的元素个数，必然都不会低于最低限制（┌ m/2 ┐ − 1）

◼ 一次分裂完毕后，有可能导致父节点上溢，依然按照上述方法解决

最极端的情况，有可能一直分裂到根节点

 

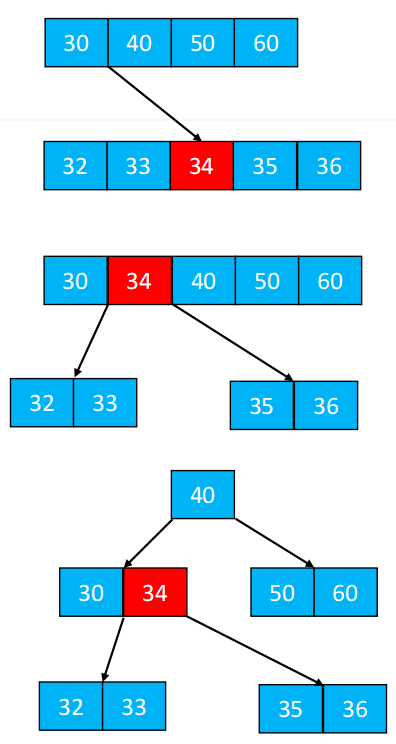
例子

 

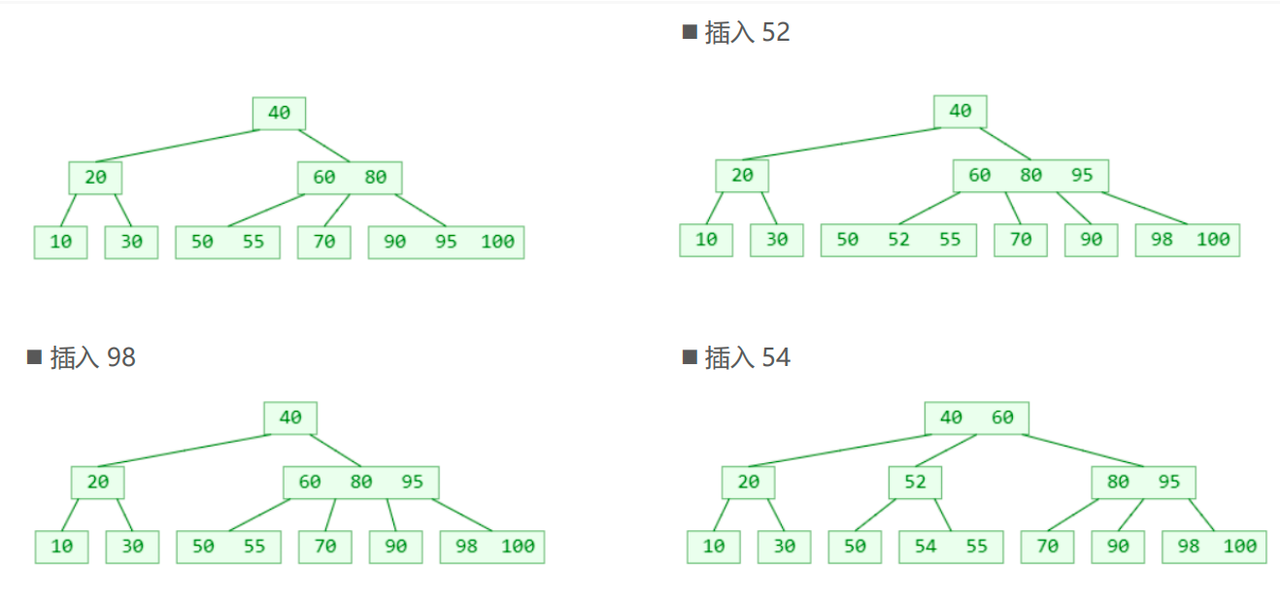
删除

1. 假如需要删除的元素在叶子节点中，那么直接删除即可

 

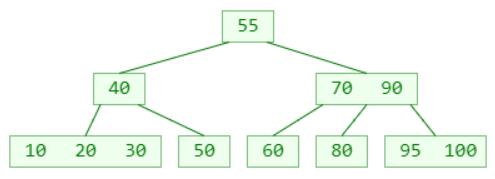
比如删除30

 

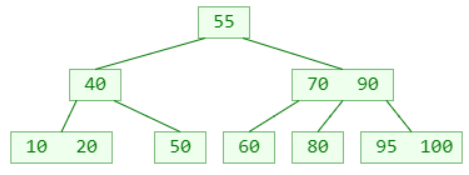
2. 假如需要删除的元素在非叶子节点中

1. 先找到前驱或后继元素，覆盖所需删除元素的值

2. 再把前驱或后继元素删除

 

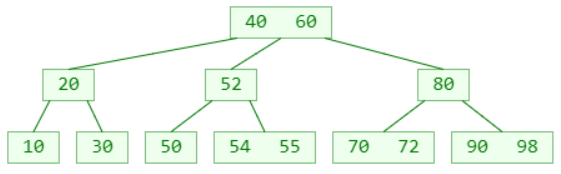
删除60

 

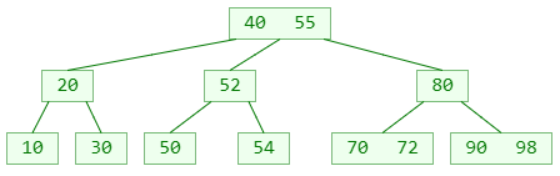
◼ 非叶子节点的前驱或后继元素，必定在叶子节点中

所以这里的删除前驱或后继元素 ，就是最开始提到的情况：删除的元素在叶子节点中

真正的删除元素都是发生在叶子节点中

3. 删除 – 下溢

 

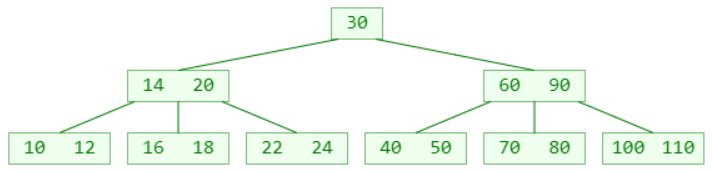
删除 22 ？（假设这是一棵 5阶B树）

叶子节点被删掉一个元素后，元素个数可能会低于最低限制（ ≥ ┌ m/2 ┐ − 1 ）

这种现象称为：下溢（underflow）

下溢的解决

◼ 下溢节点的元素数量必然等于 ┌ m/2 ┐ − 2

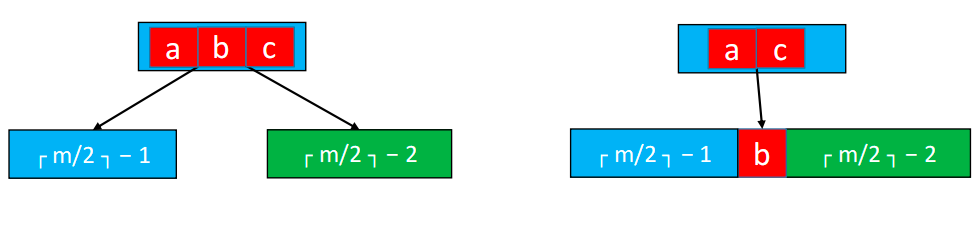
◼ 如果下溢节点临近的兄弟节点，有至少 ┌ m/2 ┐ 个元素，可以向其借一个元素

将父节点的元素 b 插入到下溢节点的 0 位置（最小位置）

用兄弟节点的元素 a（最大的元素）替代父节点的元素 b

这种操作其实就是：旋转

 

如果下溢节点临近的兄弟节点，只有 ┌ m/2 ┐ − 1 个元素

将父节点的元素 b 挪下来跟左右子节点进行合并

合并后的节点元素个数等于┌ m/2 ┐ + ┌ m/2 ┐ − 2，不超过 m − 1

这个操作可能会导致父节点下溢，依然按照上述方法解决，下溢现象可能会一直往上传播