算法：前缀和
前缀和
一、介绍
前缀和算法是一种数据预处理方法，可用于快速求数组的区间和。前缀和是一种典型的空间换时间思想的应用。
前缀和可以简单地理解为数组的前 i 个元素的和，当然其具体可以应用在一维以及二维的数组中：
- 快速求数组前 i 项之和
- 快速求数组的 [i,j] 范围内的和
- 快速求二维矩阵中某个子矩阵之和
二、场景引入
问题： 1480. 一维数组的动态和
给你一个数组 nums 。数组「动态和」的计算公式为：runningSum[i] = sum(nums[0]...nums[i]) 。请返回 nums 的动态和。
输入：nums = [1,2,3,4]
输出：[1,3,6,10]
解释：动态和计算过程为 [1, 1+2, 1+2+3, 1+2+3+4] 。
【暴力求解】
class Solution(object):
def runningSum(self, nums):
N = len(nums)
preSum = [0] * N
for i in range(N):
curSum = 0
for j in range(i + 1):
curSum += nums[j]
preSum[i] = curSum
return preSum
所求的 preSum 中每一项 preSum[i] 为累加数组位置 0 到位置 i 的元素。这样的时间复杂度为 O(n^2)，不难发现，对于每一个计算 preSum[i] 都会从位置 0 开始计算一遍，实际上，很容易观察到 preSum[i] = preSum[i-1] + nums[i]，即每个位置上的和只需用通过前一个位置的和加上当前位置的元素即可，于是通过这种计算方式，我们得到了前缀和数组。
前缀和 就是从 nums 数组中的第 0 位置开始，累加到第 i 位置的结果，我们常把这个结果保存到数组 preSum 中，记为 preSum[i]。
【前缀和求解】
class Solution(object):
def runningSum(self, nums):
N = len(nums)
preSum = [0] * N
for i in range(N):
if i == 0:
preSum[i] = nums[i]
else:
preSum[i] = preSum[i - 1] + nums[i]
return preSum
这样，时间复杂度降为 O(n)。有了前缀和数组，我们就可以快速得到数组的区间和。
- 数组 [0,i] 区间和：preSum[i]
- 数组 [i,j] 区间和：preSum[j] - preSum[i-1]
但是，在计算 [i,j] 区间和时，若 i 为 0 得单独讨论，否则 i-1 小于 0 会越界。为了让两种区间使用同一种计算公式，使用前缀和算法时，通常会令前缀和数组的长度为原数组的长度加一，使preSum[0] = 0。从而前缀和定义为：
preSum[i] = nums[0] + nums[1] + ... + nums[i-1]
则对于前缀和数组的任一项有：preSum[i] = preSum[i-1] + nums[i-1]，此时只需谨记前缀和数组的下标与原数组下标不是直接对应，而是加一对应。即 preSum[i] 表示 nums 前 i-1 项的，不包含当前元素 nums[i]。
那么，对于任意 i<=j<len(nums) ，数组 [i,j] 区间和公式：
sum(i, j) = preSum[j + 1] - preSum[i]
- preSum[j+1]：数组 nums 中 [0,j] 区间的元素和，包含 0 和 j。
- preSum[i]： 数组 nums 中 [0,i-1] 区间的元素和。
- 二者相减，即剩余数组 [i,j] 区间的元素和，包含 i 和 j。
- 当 "i==j" 时，结果即为 nums[i]/nums[j]
因此前缀和算法模板代码如下：
class Solution(object):
def runningSum(self, nums):
N = len(nums)
preSum = [0] * (N + 1)
for i in range(N):
preSum[i + 1] = preSum[i] + nums[i]
return preSum
或者不通过数组长度得到前缀和数组：
class Solution(object):
preSum=[0]
for num in nums:
preSum.append(preSum[-1]+num)
return preSum
以上为一维数组前缀和算法，二维数组前缀和可见下文例题。
三、前缀和解题流程
1.何时使用前缀和算法？
当题目中涉及区间和，前缀和为首选解决方案，子数组即为数组的区间表示。通常对于连续子数组的处理为双指针和滑动窗口，但当没有明确的指针移动判断条件时，可以尝试使用前缀和算法。
2.解题流程
前缀和思想比较简单，通常分两个步骤：
（1）预处理得到前缀和数组 preSum。即通过原数组先求得前缀和数组。
（2）根据前缀和数组计算数组中某个区间和，其中最需要注意就是使用位置下标时，前缀和数组和原数组下标之间的关系。
四、实例
一维数组
1. 题目链接：303. 区域和检索 - 数组不可变
给定一个整数数组 nums，处理以下类型的多个查询:
计算索引 left 和 right （包含 left 和 right）之间的 nums 元素的 和 ，其中 left <= right
实现 NumArray 类：
NumArray(int[] nums) 使用数组 nums 初始化对象
int sumRange(int i, int j) 返回数组 nums 中索引 left 和 right 之间的元素的 总和 ，包含 left 和 right 两点（也就是 nums[left] + nums[left + 1] + ... + nums[right] )
[题目分析]：该题目就是对前缀和数组定义的简单应用，直接求数组某个区间和。
[算法]：先根据原数组求得前缀和数组，然后求数组 [left,right] 区间和，根据区间和公式 preSum[right+1] - preSum[left] 求区间和。
点击查看代码
class NumArray:
def __init__(self, nums: List[int]):
#求得前缀和数组
self.preSum=[0]
for num in nums:
self.preSum.append(self.preSum[-1]+num)
def sumRange(self, left: int, right: int) -> int:
#前缀和数组求区间和
return self.preSum[right+1]-self.preSum[left]
[复杂度分析]：
- 时间复杂度：T(n)=O(n)，n 为数组 nums 的长度。
- 空间复杂度：S(n)=O(n)，前缀和数组空间。
2. 题目链接：724. 寻找数组的中心下标
给你一个整数数组 nums ，请计算数组的 中心下标 。
数组 中心下标 是数组的一个下标，其左侧所有元素相加的和等于右侧所有元素相加的和。
如果中心下标位于数组最左端，那么左侧数之和视为 0 ，因为在下标的左侧不存在元素。这一点对于中心下标位于数组最右端同样适用。
如果数组有多个中心下标，应该返回 最靠近左边 的那一个。如果数组不存在中心下标，返回 -1 。
[题目分析]：题中“中心下标”为：存在某个下标 i，数组 [0, i-1] 的区间和与 [i+1, n-1] 的区间和相同。因此可以通过前缀和算法解决。
[算法]：先求得前缀和数组 preSum，然后遍历一遍前缀和数组，以前缀和数组为基准，即下标从 1 到 n，找到preSum[i-1] == preSum[n] - preSum[i]的下标，返回 i-1，原数组和前缀和数组下标关系，下标 i 是前缀和数组的下标，而前缀和数组下标与原数组下标关系为加一，因此返回 i-1；若没找到则返回 -1。
点击查看代码
class Solution:
def pivotIndex(self, nums: List[int]) -> int:
preSum,n=[0],len(nums)
#前缀和数组
for num in nums:
preSum.append(preSum[-1]+num)
#区间和
for i in range(1,n+1):
if preSum[i-1]==preSum[-1]-preSum[i]:
return i-1
return -1
[复杂度分析]：
- 时间复杂度：T(n)=O(n)，n 为数组nums的长度。
- 空间复杂度：S(n)=O(n)，前缀和数组空间。
[优化]:
前缀和数组一定要求出来吗？因为题中的区间和有两个，一个是 [0,i-1] 区间和，另一个是 [i+1,n-1] 区间和。两个区间和的计算实际上只与当前位置的前缀和以及位置 n-1 的前缀和，即整个数组的和有关，因为 [i+1,n-1] 的区间和可以通过 数组和减去当前位置 i 的前缀和得到，而 [0,i-1] 的区间和可以通过当前位置 i 的前缀和减去当前位置的元素 nums[i] 即可得到。因此，不用使用空间保存所有位置的前缀和，只用常量空间计算得到当前位置的前缀和即可，通过累加就可得到。
点击查看代码
class Solution:
def pivotIndex(self, nums: List[int]) -> int:
#数组和表示 [0,n-1] 的区间和
preSum,total=0,sum(nums)
n=len(nums)
for i in range(n):
#累加计算当前位置的前缀和
preSum+=nums[i]
#[0,i-1] 区间和即为 preSum-nums[i]
#[i+1,n-1] 区间和即为 total-preSum
if preSum-nums[i]==total-preSum:
return i
return -1-1
return -1
[复杂度分析]：
- 时间复杂度：T(n)=O(n)，n 为数组nums的长度。
- 空间复杂度：S(n)=O(1)。
不使用额外空间保存前缀和数组，降低算法空间复杂度。而且不适用前缀和数组，也就不存在容易出错的下标关系问题。在针对不用使用所有位置的前缀和的情况下，可以使用常量空间表示前缀和。
3. 题目链接：560. 和为 K 的子数组
给你一个整数数组 nums 和一个整数 k ，请你统计并返回 该数组中和为 k 的子数组的个数 。
[题目分析]：看见子数组首先就想到双指针和滑动窗口，看似可以通过维护一个可变窗口，窗口中元素和为 k，但数组不是有序，即当窗口中的数大于 k 时，移动右指针以及移动左指针都可能使得元素和变小，也就是没有明确的指针移动判断条件，因此无法通过滑动窗口解决。
既然是求和为 k 的子数组，也就是区间和为 k，则可以考虑前缀和算法，通过前缀和数组，寻找区间 [i,j] 和为 k 的即可。前缀和数组，若当前位置的前缀和大小为 s，我们需要在此位置之前找到前缀和大小为 s-k 的位置，或者在此位置之后找到前缀和大小为 s+k 的位置。但，原数组无序且有正有负，因此前缀和数组也无序，则无法使用二分法快速找到位置。
快速定位，我们首先想到的就是哈希表，将所有前缀和以及其个数存入哈希表中，对于前缀和 s 能够快速找到前缀和 s+k 和 s-k 的个数，但是无法得到这两种前缀和的位置，因为 s-k 只可在当前位置之前才有效，s+k 在之后才可以。通过实例 2，我们可以不先求出前缀和数组，从前往后遍历原数组，只记录当前位置的前缀和，但是要记录该前缀和个数，那么我们可以快速找到前缀和 s-k的个数，且这些前缀和一定是在当前位置之前的，因为是从前往后遍历。而对于 s+k 的前缀和，当遍历到那个位置，当前位置即为其所需的 s-k 的位置，不会遗漏。
[算法]：使用 “前缀和+哈希” 的方法，遍历原数组，计算当前位置的前缀和 preSum，若 preSum - k 存在，则将其存在的个数加入结果，无论是否存在最后再把其个数加一。但既然使用到前缀和，那么前缀和数组的第一项为 0，那么哈希表初始化也应该是 "dic = {0:1}"，而且添加 0，也很好的处理了边缘数据的情况。
点击查看代码
class Solution:
def subarraySum(self, nums: List[int], k: int) -> int:
#【前缀和+哈希】
preSum=res=0
dic=defaultdict(int)
#前缀和数组首项 0，先存放如哈希表中
dic[0]+=1
for num in nums:
preSum+=num
if dic[preSum-k]:
res+=dic[preSum-k]
dic[preSum]+=1
return res
[复杂度分析]：
- 时间复杂度：T(n)=O(n)，n 为数组 nums 的长度。
- 空间复杂度：S(n)=O(n)，哈希表空间。
【类似题目】
3.1 题目链接：523. 连续的子数组和
给你一个整数数组 nums 和一个整数 k ，编写一个函数来判断该数组是否含有同时满足下述条件的连续子数组：
子数组大小 至少为 2 ，且
子数组元素总和为 k 的倍数。
如果存在，返回 true ；否则，返回 false 。
如果存在一个整数 n ，令整数 x 符合 x = n * k ，则称 x 是 k 的一个倍数。0 始终视为 k 的一个倍数。
[题目分析]：该题整体思路与实例 3 相同，使用哈希表存放前缀和，对于当前位置的前缀和 s，如果存在前缀和 q，有 s-q 为 k 的倍数。很明显，k 不是一个确定的数，而是多个不同数的集合，此时如果再使用实例 3 中相同方法则无法实现（超时，因为要把 s 减去所有小于s的 k 的倍数都计算一遍）。
我们可以将每个位置的前缀和对 k 取余的结果存放在哈希表，若存在一个连续子数组的和为 k，那么该连续子数组的前一个位置的前缀和对 k 取余的结果和该连续子数组最后一个元素位置的前缀和对 k 取余的结果相同。
如 [23, 2, 4, 6, 7]，k = 6，其前缀和 preSum=[0, 23, 25, 29, 35, 42]，原数组中 [2, 4] 区间和为6，该区间前一个位置的前缀和为 preSum[1] = 23，23 % 6 = 5。而该区间最后一个元素位置的前缀和为 preSum[3] = 29，29 % 6 = 5。区间 [2, 4] 换成任意和为 6 的倍数的两个数，结果都是相同。即通过模 6 的方法解决了直接使用 6 的倍数但为不确定数的情况。
[算法]：同样使用 “哈希表 + 前缀和” 的方法，与实例 3 不同的是，哈希表中存放的是前缀和模 k 的结果与当前前缀和位置的键值对，因为我们只需判断是否存在满足条件的子数组，且该子数组的长度大于等于 2，因此需要通过下标判断子数组长度是否满足条件。可以不用求前缀和，只通过之前的余数加上当前元素的和模 k，效果与前缀和模 k 相同。若模 k 的结果在哈希表中，且长度大于 1，则直接返回 True；如果不存在，则将该结果和当前位置加入哈希表中。
点击查看代码
class Solution:
def checkSubarraySum(self, nums: List[int], k: int) -> bool:
#前缀和首项为 0，因此余数为 0，其位置为 0
dic,remind={0:0},0
for idx,num in enumerate(nums):
remind=(remind+num)%k
jdx=dic.get(remind)
#结果存在，则判断子数组长度
if jdx!=None:
if idx-jdx>0:
return True
#不存在则加入哈希表
else:
dic[remind]=idx+1
return False
[复杂度分析]：
- 时间复杂度：T(n)=O(n)，n 为数组 nums 的长度。
- 空间复杂度：S(n)=O(n)，哈希表空间。
3.2 题目链接：525. 连续数组
给定一个二进制数组 nums , 找到含有相同数量的 0 和 1 的最长连续子数组，并返回该子数组的长度。
[题目分析]：一开始会想到维护一个大小可变的滑动窗口，窗口中 0，1 个数相等。但是当个数不相等时，移动左右指针都可能使得个数相等，因此无法使用滑动窗口。如果直接使用前缀和，0，1 个数相等的区间 [i, j] 情况是：j - i + 1 == 2 * (preSum[j+1] - preSum[i])，其中位置 i 和 preSum[i] 都不确定，可以依次尝试判断，但时间复杂度高。
因此可以做一种特殊处理，因为数组中只有 0、1，那么对于 0，前缀和可以进行减一操作，对于 1，就正常的加一操作。那么0，1 个数相等的区间 [i, j] 情况是：preSum[j+1] == preSum[i]，这样通过哈希表就很容易查找到。
[算法]：仍然使用 “哈希表 + 前缀和” 的方法，前缀和的操作就如上面的特殊处理。当当前前缀和存在则更新最大长度结果；如果不存在，则存入哈希表。这里只有当前缀和不存在时才存入位置，多次出现的前缀和只保存首次出现的位置，这样也保证了最长子数组的要求。
点击查看代码
class Solution:
def findMaxLength(self, nums: List[int]) -> int:
res=preSum=0
dic={0:0}
for idx,num in enumerate(nums):
preSum +=1 if num else -1
jdx=dic.get(preSum)
if jdx!=None:
res=max(res,idx+1-jdx)
else:
dic[preSum]=idx+1
return res
[复杂度分析]：
- 时间复杂度：T(n)=O(n)，n 为数组 nums 的长度。
- 空间复杂度：S(n)=O(n)，哈希表空间。
4. 题目链接：1588. 所有奇数长度子数组的和
给你一个正整数数组 arr ，请你计算所有可能的奇数长度子数组的和。
子数组 定义为原数组中的一个连续子序列。
请你返回 arr 中 所有奇数长度子数组的和 。
[题目分析]：子数组和即区间和，通过前缀和可求得。而要所有奇数长度的区间和，当求得区间和后，可通过固定大小的滑动窗口，大小为小于等于数组长度的所有奇数，求得每个窗口的区间和即可。
[算法]：先求得前缀和数组，在求的同时，可以先将所有元素相加存入结果，相当于所有长度为 1 的子数组的区间和。然后从 3 开始一直到 数组长 n,求得所有奇数大小区间的区间和。
点击查看代码
class Solution:
def sumOddLengthSubarrays(self, arr: List[int]) -> int:
preSum,res=[0],0
for num in arr:
#区间大小为 1 的和
res+=num
preSum.append(preSum[-1]+num)
n=len(arr)
#窗口大小为奇数，且从大小为 3 开始
for j in range(3,n+1,2):
i=0
#窗口滑动，计算区间和
while j<=n:
res+=preSum[j]-preSum[i]
i+=1
j+=1
return res
[复杂度分析]：
- 时间复杂度：T(n)=O(n^2)，n 为数组 arr 的长度。
- 空间复杂度：S(n)=O(n)，前缀和数组空间。
5. 题目链接：238. 除自身以外数组的乘积
给你一个整数数组 nums，返回 数组 answer ，其中 answer[i] 等于 nums 中除 nums[i] 之外其余各元素的乘积 。
题目数据 保证 数组 nums之中任意元素的全部前缀元素和后缀的乘积都在 32 位 整数范围内。
请不要使用除法，且在 O(n) 时间复杂度内完成此题。
[题目分析]：前缀和的拓展应用，即前缀积。原理以及方法和前缀和相同，求得数组的正反向的两个前缀积数组，然后一个从前往后，一个从后往前对应位置的前缀积相乘，直至二者位置相遇。
[算法]：根据之前前缀和算法中不用求出前缀和数组，可以只求一个正向的前缀积，另一个反向的前缀积可以累乘只计算当前所需的前缀积。
点击查看代码
class Solution:
def productExceptSelf(self, nums: List[int]) -> List[int]:
preCu,posCu=[1],[1]
res=[]
n=len(nums)
#正向数组的前缀积数组
for num in nums:
preCu.append(preCu[-1]*num)
t=1
for i in range(n):
res.append(preCu[n-i-1]*t)
#反向数组的前缀积
t*=nums[n-i-1]
return res[::-1]
[复杂度分析]：
- 时间复杂度：T(n)=O(n^2)，n 为数组 nums 的长度。
- 空间复杂度：S(n)=O(n)，前缀积数组空间。
6. 题目链接：497. 非重叠矩形中的随机点
给定一个由非重叠的轴对齐矩形的数组 rects ，其中 rects[i] = [ai, bi, xi, yi] 表示 (ai, bi) 是第 i 个矩形的左下角点，(xi, yi) 是第 i 个矩形的右上角点。设计一个算法来随机挑选一个被某一矩形覆盖的整数点。矩形周长上的点也算做是被矩形覆盖。所有满足要求的点必须等概率被返回。
在给定的矩形覆盖的空间内的任何整数点都有可能被返回。
请注意 ，整数点是具有整数坐标的点。
[题目分析]：题目的关键，选择矩形的点必须等概率被返回。这里的等概率，首先要等概率得选择矩形，然后再等概率得选择矩形中的点。
1.如何等概率选择矩形中的点？
假设有三个矩形，其中分别有 a、b、c 个点，当已经选择了第一个矩形，之后选择矩形中的点的概率均为 1/a，其余两个分别为 1/b 和 1/c。而如果等概率选择矩形，即均为 1/3，则选择三个矩形中点的概率分别为 1/3 * 1/a、 1/3 * 1/b、 1/3 * 1/c，三者不相等。因此选择矩形时要分概率选择，根据矩形中的点个数，每个矩阵选择的概率分别为 a/a+b+c、b/a+b+c、c/a+b+c，而后再选择每个点的概率均为 1/a+b+c。
2.如何返回矩形中的点？
用正数点编号表示矩形，每个矩形的点数根据其左上角坐标 (x1,y1) 和右下角坐标 (x2,y2) 可求得：(x2-x1+1)*(y2-y1+1)
使用矩阵的点数构成数组，然后求得其前缀和数组，从 1 至最大前缀和之间随机选择一个数，通过二分法找到该点属于对应的哪个矩形，最后根据该矩形的长宽，分别在长宽的范围内随机选择一个数作为矩阵中的点返回。
点击查看代码
class Solution:
def __init__(self, rects: List[List[int]]):
self.rects=rects
self.preSum=[0]
#矩阵点数构成数组并求其前缀和数组
for idx,(x1,y1,x2,y2) in enumerate(rects):
self.preSum.append(self.preSum[-1]+(x2-x1+1)*(y2-y1+1))
def pick(self) -> List[int]:
#在所有点数中随机选择一个编号
ch=random.randint(1,self.preSum[-1])
#查找该编号属于哪个矩阵
idx=bisect.bisect_left(self.preSum,ch)
[x1,y1,x2,y2]=self.rects[idx-1]
return [random.randint(x1,x2),random.randint(y1,y2)]
[复杂度分析]：
- 时间复杂度：构造函数复杂度为 O(n)，pick 函数复杂度为 O(logn)，其中 n 为 rects 的长度。构造函数需要构造前缀和数组，pick 函数需要在前缀和数组内进行二分。
- 空间复杂度：构造函数复杂度为 O(n)，pick 函数复杂度为 O(1)，其中 n 为 rects 的长度。构造函数需要构造前缀和数组，pick 函数只需要使用常数空间。
7. 题目链接：1744. 你能在你最喜欢的那天吃到你最喜欢的糖果吗？
[题目分析]：该题主要在于理解题意，只有两种情况在第 favoriteDay 吃不到糖果：
1. 每天吃一颗，favoriteDay-1 天已经把前 favoriteType 类的糖果吃完了
2. 每天吃 dailyCap 颗，第 favoriteDay 天还没把前 favoriteType-1 类的糖果吃完
吃到糖果，即在第 favoriteDay 天吃到第 favoriteType 类的糖果。主要注意天数，第0天开始吃。
[算法]：前缀和数组是解决该题的工具，主要需判断上述两个条件是否满足即可。
点击查看代码
class Solution:
def canEat(self, candiesCount: List[int], queries: List[List[int]]) -> List[bool]:
preSum,res=[0],[]
for cn in candiesCount:
preSum.append(preSum[-1]+cn)
for query in queries:
ft,fd,dc=query[0],query[1],query[2]
if fd>=preSum[ft+1] or (fd+1)*dc<=preSum[ft]:
res.append(False)
else:
res.append(True)
return res
[复杂度分析]：
- 时间复杂度：O(n+q)，其中 n 和 q 分别是数组 candiesCount 和 queries 的长度。
- 空间复杂度：S(n)=O(n)，前缀和空间。
二维数组
1. 题目链接：304. 二维区域和检索 - 矩阵不可变
给定一个二维矩阵 matrix，以下类型的多个请求：
计算其子矩形范围内元素的总和，该子矩阵的 左上角 为 (row1, col1) ，右下角 为 (row2, col2) 。
实现 NumMatrix 类：
NumMatrix(int[][] matrix) 给定整数矩阵 matrix 进行初始化
int sumRegion(int row1, int col1, int row2, int col2) 返回 左上角 (row1, col1) 、右下角 (row2, col2) 所描述的子矩阵的元素 总和 。
示例 1：
输入:
["NumMatrix","sumRegion","sumRegion","sumRegion"]
[[[[3,0,1,4,2],[5,6,3,2,1],[1,2,0,1,5],[4,1,0,1,7],[1,0,3,0,5]]],[2,1,4,3],[1,1,2,2],[1,2,2,4]]
输出:
[null, 8, 11, 12]
解释:
NumMatrix numMatrix = new NumMatrix([[3,0,1,4,2],[5,6,3,2,1],[1,2,0,1,5],[4,1,0,1,7],[1,0,3,0,5]]);
numMatrix.sumRegion(2, 1, 4, 3); // return 8 (红色矩形框的元素总和)
numMatrix.sumRegion(1, 1, 2, 2); // return 11 (绿色矩形框的元素总和)
numMatrix.sumRegion(1, 2, 2, 4); // return 12 (蓝色矩形框的元素总和)
[题目分析]：对于二维数组的前缀和与一维一样，先求前缀和数组，再求区间和。
1.求前缀和数组
二维数组的前缀和同样使用二维数组表示。preSum[i][j] 表示从 [0, 0] 到 [i, j] 的子矩阵元素和，其递推公式如下：
preSum[i][j]=preSum[i−1][j]+preSum[i][j−1]−preSum[i−1][j−1]+matrix[i][j]
可通过下图理解：
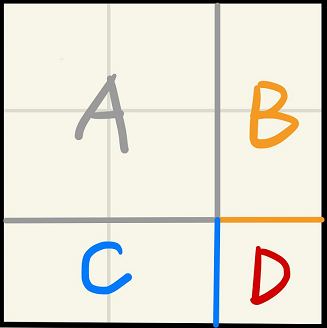
要计算整个矩形的面积 S 大小为 preSum[i][j]，图中 A + B 的面积大小为 preSum[i−1][j]，A + C 的面积大小为 preSum[i][j−1]，A 的面积大小为 preSum[i−1][j−1]，D 的面积大小为 matrix[i][j]。则整个矩形的面积 S = S(A,B) + S(A,C) - S(A) + S(D)，用具体的数值表示后即为上述公式。
2.求区间和（子矩阵面积）
子矩阵可用左上角坐标 [row1, col1] 和右下角坐标 [row2, col2]，两个坐标表示，则此区域内元素和为：
preSum[row2][col2]−preSum[row2][col1−1]−preSum[row1−1][col2]+preSum[row1−1][col1−1]
此过程相当于上面图中求 S(D) 的过程一样，S(D) = S - S(A,B) - S(A,C) + S(A)，带入具体数值即为上述公式。
点击查看代码
class NumMatrix:
def __init__(self, matrix: List[List[int]]):
n,m=len(matrix[0]),len(matrix)
#二维前缀和数组初始化，边界为0，于一维同理
self.preSum=[[0 for _ in range(n+1)] for _ in range(m+1)]
for i in range(1,m+1):
for j in range(1,n+1):
self.preSum[i][j]=self.preSum[i][j-1]+self.preSum[i-1][j]+matrix[i-1][j-1]-self.preSum[i-1][j-1]
def sumRegion(self, row1: int, col1: int, row2: int, col2: int) -> int:
#直接代入公式
return self.preSum[row2+1][col2+1]-self.preSum[row2+1][col1]-self.preSum[row1][col2+1]+self.preSum[row1][col1]
[复杂度分析]：
- 时间复杂度：T(n)=O(n * m)，m、n 分别为二维数组 matrix 的行数、列数。
- 空间复杂度：S(n)=O(n * m)。
