洛谷P3237 [HNOI2014]米特运输（树形dp）

解题报告

题干

米特是D星球上一种非常神秘的物质，蕴含着巨大的能量。在以米特为主要能源的D星上，这种米特能源的运输和储存一直是一个大问题。

D星上有N个城市，我们将其顺序编号为1到N，1号城市为首都。这N个城市由N-1条单向高速通道连接起来，构成一棵以1号城市（首部）为根的树，高速通道的方向由树中的儿子指向父亲。树按深度分层：根结点深度为0，属于第1层；根结点的子节点深度为1，属于第2层；依此类推，深度为i的结点属于第i+l层。

建好高速通道之后，D星人开始考虑如何具体地储存和传输米特资源。由于发展程度不同，每个城市储存米特的能力不尽相同，其中第i个城市建有一个容量为A[i]的米特储存器。这个米特储存器除了具有储存的功能，还具有自动收集米特的能力。

如果到了晚上六点，有某个储存器处于未满的状态，它就会自动收集大气中蕴含的米特能源，在早上六点之前就能收集满；但是，只有在储存器完全空的状态下启动自动收集程序才是安全的，未满而又非空时启动可能有安全隐患。

早上六点到七点间，根节点城市（1号城市）会将其储存器里的米特消耗殆尽。根节点不会自动搜集米特，它只接受子节点传输来的米特。

早上七点，城市之间启动米特传输过程，传输过程逐层递进：先是第2层节点城市向第1层（根节点城市，即1号城市）传输，直到第1层的储存器满或第2层的储存器全为空；然后是第3层向第2层传输，直到对于第2层的每个节点，其储存器满或其予节点（位于第3层）的储存器全为空；依此类推，直到最后一层传输完成。传输过程一定会在晚上六点前完成。

由于技术原因，运输方案需要满足以下条件：

1. 不能让某个储存器到了晚上六点传输结束时还处于非空但又未满的状态，这个时候储存器仍然会启动自动收集米特的程序，而给已经储存有米特的储存器启动收集程序可能导致危险，也就是说要让储存器到了晚上六点时要么空要么满；
2. 关于首都——即1号城市的特殊情况， 每天早上六点到七点间1号城市中的米特储存器里的米特会自动被消耗殆尽，即运输方案不需要考虑首都的米特怎么运走；
3. 除了1号城市，每个节点必须在其子节点城市向它运输米特之前将这座城市的米特储存器中原本存有的米特全部运出去给父节点，不允许储存器中残存的米特与外来的米特发生混合；
4. 运向某一个城市的若干个来源的米特数量必须完全相同，不然，这些来源不同的米特按不同比例混合之后可能发生危险。

现在D星人已经建立好高速通道，每个城市也有了一定储存容量的米特储存器。为了满足上面的限制条件，可能需要重建一些城市中的米特储存器。你可以，也只能，将某一座城市（包括首都）中原来存在的米特储存器摧毁，再新建一座任意容量的新的米特储存器，其容量可以是小数（在输入数据中，储存器原始容量是正整数，但重建后可以是小数），不能是负数或零，使得需要被重建的米特储存器的数目尽量少。

Input

第一行是一个正整数N，表示城市的数目。
接下来N行，每行一个正整数，其中的第i行表示第i个城市原来存在的米特储存器的容量。
再接下来是N-I行，每行两个正整数a，b表示城市b到城市a有一条高速通道(a≠b)。

Output

输出文件仅包含一行，一个整数，表示最少的被重建（即修改储存器容量）的米特储存器的数目。

Sample Input

5
5
4
3
2
1
1 2
1 3
2 4
2 5

Sampe Output

​ 3

样例解释

一个最优解是将A[1]改成8，A[3]改成4，A[5]改成2。这样，2和3运给1的量相等，4和5运给2的量相等，且每天晚上六点的时候，1，2满，3，4，5空，满足所有限制条件。

对于100%的数据满足N<500000，A[j]<10^8

整活

全题最难的依然是花里胡哨的题干。仔细研究半天能总结出这题的意思是：

• 给出一棵树，节点带权，修改最少的点权，使树满足以下两个条件：
  1. 同一个父亲的儿子权值都相同
  2. 父亲的取值为所有的儿子的权值之和（其实转化一下也就是它的子树里所有节点的权值和）

这样这棵树有一个很好的性质，对于某一个点，它的权值确定了，那么他所对应的整颗树就可以确定了。所以这道题我们用了一下逆向思维，不是通过修改树来统计点，而是通过某一个点反推出它所对应的整棵树，通过看能反推出同一棵树的点有多少个，计算最少修改点。假如我们有sum个点能推出同一棵树，那么显然要修改的点即为n-sum个。

那么这个反推我们是通过权值来实现的，我们定义f[x]的值为，保留x节点，他所对应的合法整棵树的根节点的权值是多少。这样f[ ]相同的点，必然来自同一种合法的树。可以想一想为什么。

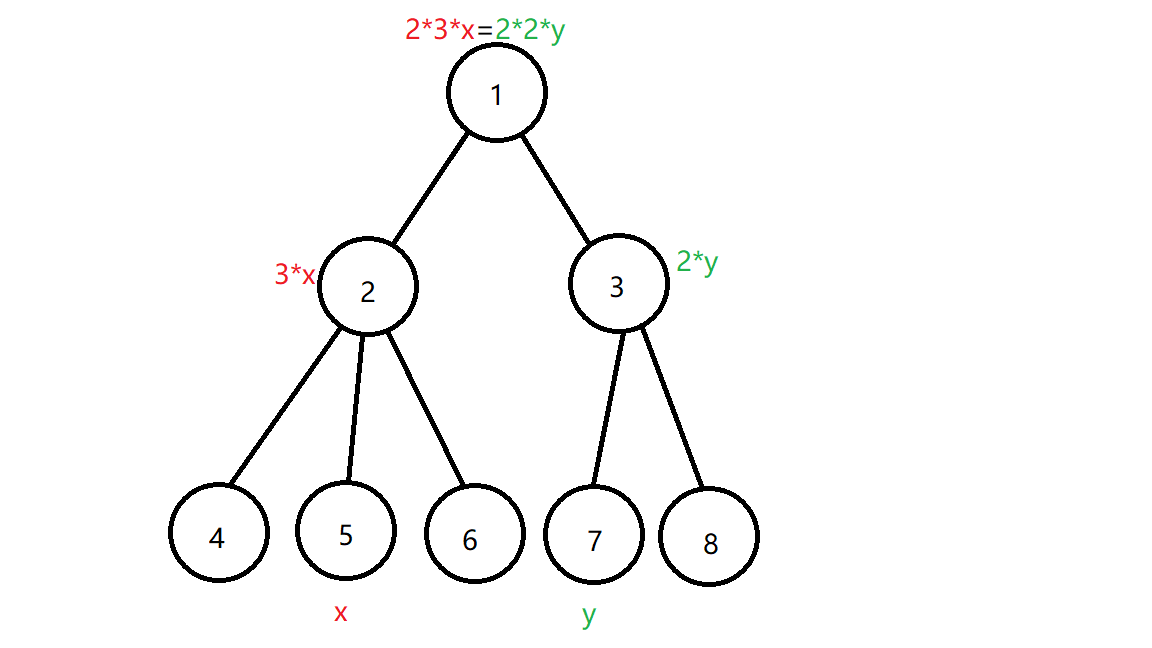
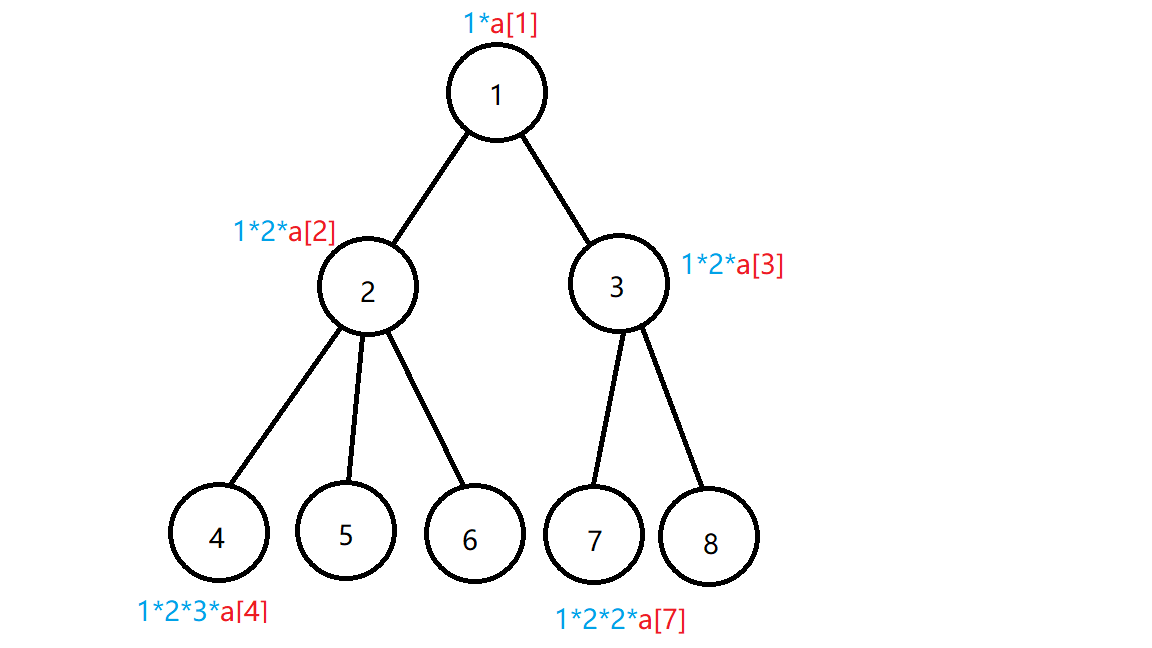
为辅助理解我嫖来两张洛谷的题解（图里的a[]就是我代码里的w[]）：

我们从上往下递归一下

递归完确定所有f[x]之后，sort一遍，把相同的都给排到一起，方便统计。

还有挺重要的一点是直接累乘的话double是存不下的，所以有一个很巧妙的方法就是加上log值，化乘为加，在不要求求具体数值的情况下可以考虑这种方法。

实现

#include<cstdio>
#include<iostream>
#include<algorithm>
#include<cstring>
#include<cmath>
using namespace std;
const int maxn=500000+1;
#define ll long long
#define Dio ios::sync_with_stdio(0)//优化cin,cout的东东，砸瓦鲁多！
double w[maxn],f[maxn],siz[maxn];
int head[maxn],len=0;
struct Edge{
    int to,next;
}edge[maxn];//这题是个有向图，所以边数不用乘2
void Add(int u,int v){
    edge[++len].next=head[u];
    edge[len].to=v;
    head[u]=len;
}
void dfs(int u,int fa,double sum){
    f[u]=sum+log(w[u]);//由于累乘权值double会爆，转化成log相加
    for(int i=head[u];i;i=edge[i].next){
        int v=edge[i].to;
        dfs(v,u,sum+log(siz[u]));//继续向下递归，向里面乘上子树个数，原理看上面的图
    }
}
int main(){
    Dio;
    int n,cnt=1,ans=0;
    cin>>n;
    for(int i=1;i<=n;i++){
        cin>>w[i];
    }
    for(int i=1;i<=n-1;i++){
        int u,v;
        cin>>u>>v;
        Add(u,v);
        siz[u]=siz[u]+1;//记录子树个数
    }
    dfs(1,0,log(1.0));
    sort(f+1,f+1+n);//sort一遍我们把所有相同的都排到一起方便统计
    for(int i=2;i<=n;i++){//找出最多有多少个相同的
        if(f[i]-f[i-1]<=1e-8){//手动补齐精度
            ans=max(ans,++cnt);
        }
        else cnt=1;//值不同说明构成的不是同一个树了，重新开始计数
    }
    cout<<n-ans<<endl;
    return 0;
}