图论做题笔记
POI2014 Rally(拓扑排序)
Description
给定一个N个点M条边的有向无环图,每条边长度都是1。
请找到一个点,使得删掉这个点后剩余的图中的最长路径最短。
\(n,m\le 5\times 10^5\)
Solution
- 令\(S_i\)表示从i结束的最长路,\(T_i\)表示由i出发的最长路
- 这两个数组的预处理可以通过拓扑排序在\(O(n)\)的时间复杂度下解决
- 然后根据拓扑序从小到大扫描一遍,每次删除和i入边有关的最长路,回答询问后,加入与i出边有关的最长路。
- 可以证明这种添加方式不会重复添加。
- 然后再利用线段树或者堆维护一下就可以了
牛客NOIP模拟第五场T2
Description
一个n节点,m条边的无向简单图 。第i条边的权值为\(2^i\) ,求一条路径能够经过所有的边至少一次,且花费最小。
- \(n,m \le 5\times 10^5\)
Solution
首先如果图满足欧拉回路的性质(所有边的度数为偶数),那么答案就是权值之和 。
不然就要通过重复走某些边【制造重边】的方式使图存在欧拉回路。
性质1:
遍历一棵树的所有边,每条边最多被遍历两次 【尽量减小遍历次数的情况下】
性质2:
对于一个权值为\(2^i\)的边,经过编号为[0,i-1]的边各一次权值和更小
根据上述的性质,建一棵最小生成树,首先它满足性质1,由于经过非树边等同于经过它在树上所构成的环,再根据性质2,可得出对于一条非树边,一定没有重复走树边更优,然后就利用回溯的方法判断某条边是否要走两遍,加上贡献,得到答案
Code
#include<cstdio>
#define FOR(i,x,y) for(int i=(x),i##_END=(y);i<=i##_END;++i)
#define DOR(i,x,y) for(int i=(x),i##_END=(y);i>=i##_END;--i)
template<const int maxn,const int maxm>struct Link_list{
int head[maxn],nxt[maxm],V[maxm],tot;
inline void add(int a,int b){nxt[++tot]=head[a];head[a]=tot;V[tot]=b;}
int& operator [] (const int &x){return V[x];}
#define LFOR(i,x,a) for(int i=(a).head[x];i;i=(a).nxt[i])
};
const int P=998244353;
const int M=500005;
Link_list<M,M<<1> E,Id;
inline void Rd(int &x){
static char c;x=0;
while(c=getchar(),c<48);
do x=(x<<3)+(x<<1)+(c&15);
while(c=getchar(),47<c);
}
int ans;
int X[M],Y[M],par[M],Pow[M],Deg[M];
int find(int x){return x==par[x]?x:par[x]=find(par[x]);}
int DFS(int x,int f){
LFOR(i,x,E){
int y=E[i];
if(y==f)continue;
if(DFS(y,x)){
Deg[x]++;
ans=(ans+Pow[Id[i]])%P;
}
}
return Deg[x]%2;
}
int main(){
int n,m,x,y;
Rd(n),Rd(m);
Pow[0]=1;
FOR(i,1,n)par[i]=i;
FOR(i,1,m){
Rd(X[i]),Rd(Y[i]);
Deg[X[i]]++,Deg[Y[i]]++;
Pow[i]=Pow[i-1]*2%P;
ans=(ans+Pow[i])%P;
}
FOR(i,1,m){
x=find(X[i]),y=find(Y[i]);
if(x==y)continue;
par[x]=y;
E.add(X[i],Y[i]),E.add(Y[i],X[i]);
Id.add(X[i],i),Id.add(Y[i],i);
}
DFS(1,0);
printf("%d\n",ans);
return 0;
}
COCI2011/2012 Contest#Final A
Description
给定\(n\)节点,\(m\)条单向边的图,求一条路径,从1出发经过2并返回1,同时满足经过的点的种类尽量少
\(n\le 100\)
Solution
首先最终答案路径大概会长成这样子:
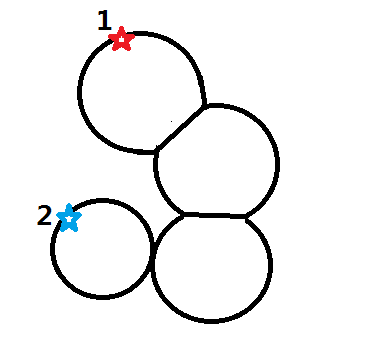
就是一个环套环的形式
定义 \(g_{i,j}\) 为\(i\)到\(j\)的最短路
定义 \(dp_{i,j}\) 为从1出发,经过 \(i,j\) 并回到1的路径最少经过点种类数 (包含终点,不包含起点)
那么就有转移方程 :\(chkmin(dp_{i,j},dp_{a,b}+g_{b,i}+g_{i,j}+g_{j,b}-1)\)
最初\(dp_{1,1}=1\) ,答案为 \(dp_{2,2}\)
思路的来源
如果图是无向图的话,那答案显然是1到2的最短路长度+1
但是这个图为有向图,所以可能不会原路返回
那么从1出发再返回1的路径可能就是一个环或者是多个环嵌套在一起(所以有时候考虑终态是一件十分重要的事情)
对于环套环,环与环之间就有公共点或者公共边,而dp的下标就是记录这个公共边[点],方便进行转移
Code
#include<bits/stdc++.h>
#define FOR(i,x,y) for(int i=(x),i##_END=(y);i<=i##_END;++i)
#define DOR(i,x,y) for(int i=(x),i##_END=(y);i>=i##_END;--i)
using namespace std;
const int M=105;
const int INF=100000000;
int dp[M][M],g[M][M];
bool use[M][M];
int main(){
int n,m;
cin>>n>>m;
FOR(i,1,n)FOR(j,1,n)g[i][j]=(i==j)?0:INF;
FOR(i,1,m){
int a,b;
scanf("%d%d",&a,&b);
g[a][b]=1;
}
FOR(k,1,n)FOR(i,1,n)FOR(j,1,n)g[i][j]=min(g[i][j],g[i][k]+g[k][j]);//floyd预处理最短路
FOR(i,1,n)FOR(j,1,n)dp[i][j]=INF;
dp[1][1]=1;
while(1){//每次至少找到不同的a,b,所以最多进行 n^2 次
int a=-1,b;
FOR(i,1,n)FOR(j,1,n){//每次找到不能再被更新的一个回路,用它来松弛其他的回路
if(use[i][j])continue;
if(a==-1||dp[a][b]>dp[i][j]){
a=i,b=j;
}
}
if(a==2&&b==2)break;
FOR(i,1,n)FOR(j,1,n){//松弛
if(i==a||i==b||j==a||j==b)continue;
dp[i][j]=min(dp[i][j],dp[a][b]+g[b][i]+g[i][j]+g[j][a]-1);
}
use[a][b]=true;//标记已被用来松弛的回路
}
printf("%d\n",dp[2][2]);
return 0;
}
YCJS3060 引水上树
Description
有一棵 \(n\) 节点的树,有 \(m\) 个询问
每次询问包含两个参数\(x,y\)
表示 \(y\) 条有公共点或者公共边的路径并且满足穿过 \(x\)
要求这 \(y\) 条路径覆盖的边权和尽量大
\(n,m\le 10^5\)
Solution
首先要推导一些性质
1.选取的路径的端点肯定是叶子节点
不然,从非叶节点扩展到叶子结点更优
那么当x为叶子节点时,等于选 \(2\times y-1\) 个叶子节点
当x为非叶子节点时,等于选\(2\times y\) 个叶子结点
2.在y=1选取的叶子节点,在y=2时也会被取
根据1,2性质,就可以得到一种写法:
从根为x的树上取一条最长链[一段为x],把它删去后,再取剩下的最长的链
直到取完
把这些路径排序,然后对于询问y,就是取前面前y条路径
那么这样的复杂度就为 \(O(q\times n\times logn)\)
如何处理这些最长链呢?
可以通过类似长链剖分的东西
设 \(x\) 的子树中的最长链是 \(son[x]\) 上来的
那么就可以用下面的代码把整棵树剖掉
void Calc(int x,int d) {
if(is_leaf[x]){//将最长链的信息记录在叶节点
A[++m]=(node){x,d};
son[x]=x;
}
LFOR(i,x,E) {
int y=E[i];
if(y==fa[x][0]) continue;
if(son[x]==y) Calc(y,d+V[i]);//最长链
else Calc(y,V[i]);//非最长链,从零开始
}
}
同时根据上面的写法,可以得到处理固定根的询问,预处理复杂度为 \(O(nlogn)\)
3.y等于任何值时,选取的叶子节点肯定至少有一个是直径的端点
这个当\(y=1\)的时候就会被当做叶子节点取到
根据第三个性质,预处理出以直径两段为根的答案
询问x时,如果被预处理好的方案包含了[有路径经过x],那么直接得到答案
如果没有被包含,就要对当前方案进行微调
一共有两种决策:
1.删除一条路径,加入穿过x的最长路径
2.删除一条路径的部分[至少有一条边不变,不然和决策一没有区别],加入穿过x的最长路径
对于决策1,只用删除那条最短的路径即可
对于决策2,被删除的路径一定经过 \(x\) 的祖先
现在考虑如何快速解决决策2
设a为x到根的路径上,最先被路径覆盖的点
那么只用考虑把a点挂下来的路径给删掉就可以了 [重点]
Q:但是但是...如果a点上面的有一个祖先b,它挂下来的路径更短,那么删去a点挂下来的路径就不能使决策2最优了
A: 如果存在这样的b,那么可以发现b到根节点的路径肯定与b挂下来的路径一定不是连在一起的,那它其实满足决策1,在决策1中已经考虑过了
那么如何快速找到这个a点?
设每个点都有被覆盖的时间 [根据路径的选取顺序]
4.在x到根的路径,点被覆盖的时间递减
所以用倍增就可以试探出最先满足条件的点了
复杂度 \(O(nlogn+qlogn)\)
Code
代码其实绝大大部分是copy的
#include<cstdio>
#include<cstring>
#include<algorithm>
#define FOR(i,x,y) for(int i=(x),i##_END=(y);i<=i##_END;++i)
#define DOR(i,x,y) for(int i=(x),i##_END=(y);i>=i##_END;--i)
using namespace std;
inline bool chk_mx(int &x,const int &y){return x<y?x=y,true:false;}
template<const int maxn,const int maxm>struct Link_list {
int head[maxn],nxt[maxm],V[maxm],tot;
void add(int a,int b){nxt[++tot]=head[a];head[a]=tot;V[tot]=b;}
int& operator [] (const int &x){return V[x];}
#define LFOR(i,x,a) for(int i=(a).head[x];i;i=(a).nxt[i])
};
const int M=100005;
Link_list<M,M<<1> E,V;
int n,q;
int Mx,D;
void FAT(int x,int f,int d) {
if(Mx<d)Mx=d,D=x;
LFOR(i,x,E) {
int y=E[i];
if(y==f) continue;
FAT(y,x,d+V[i]);
}
}
struct Tree {
static const int S=18;
int son[M],dis[M],mx[M],fa[M][S],rt;
int Ans[M],Tim[M];
bool is_leaf[M];
struct node {
int p,d;
bool operator <(const node &_)const {
return d>_.d;
}
}A[M];
int m;
void DFS(int x,int f,int d) {
dis[x]=d,fa[x][0]=f;
is_leaf[x]=true;
LFOR(i,x,E) {
int y=E[i];
if(y==f) continue;
is_leaf[x]=false;
DFS(y,x,d+V[i]);
if(chk_mx(mx[x],mx[y]+V[i])) son[x]=y; //最长链是从哪个儿子上来的
}
}
void Calc(int x,int d) {
if(is_leaf[x]){//到叶子节点
A[++m]=(node){x,d};
son[x]=x;
}
LFOR(i,x,E) {
int y=E[i];
if(y==fa[x][0]) continue;
if(son[x]==y) Calc(y,d+V[i]);
else Calc(y,V[i]);
}
son[x]=son[son[x]];//这里顺便改变son[x]表示的东西,这里可以认为表示穿过x点的路径编号
}
void Init() {
DFS(rt,0,0);
Calc(rt,0);
sort(A+1,A+m+1);
FOR(i,1,m) {
Ans[i]=Ans[i-1]+A[i].d;//取i条路径时的答案
Tim[A[i].p]=i;//这条路径在取多少条路径时才会被取到
}
FOR(j,1,S-1) FOR(i,1,n)
fa[i][j]=fa[fa[i][j-1]][j-1];
}
int Query(int x,int y){
y=min(y,m);
if(Tim[son[x]]<=y) return Ans[y];//本身方案覆盖x,那么就直接返回
//调整使得方案包含x且尽量大
int s=son[x];//先存下x的最长链
DOR(i,S-1,0)
if(fa[x][i] && Tim[son[fa[x][i]]]>y)
x=fa[x][i];
x=fa[x][0];//当前的x为距离询问的x最近被覆盖的祖先
return Ans[y]-min(A[y].d,dis[son[x]]-dis[x])+dis[s]-dis[x];
//A[y].d为决策一,dis[son[x]]-dis[x]为上面推导的决策二
//dis[s]-dis[x]为穿过x最长的路径,可以证明是合法的
}
}T[2];
int main() {
scanf("%d%d",&n,&q);
FOR(i,2,n) {
int a,b,c;
scanf("%d%d%d",&a,&b,&c);
E.add(a,b),V.add(a,c);
E.add(b,a),V.add(b,c);
}
FAT(1,0,0);//找直径部分 FAT表示fat_tiger的f1函数
T[0].rt=D,Mx=0;
FAT(D,0,0);
T[1].rt=D;
T[0].Init();
T[1].Init();
while(q--) {
int x,y;
scanf("%d%d",&x,&y);
y=y*2-1; //首先直径的两段就为叶子节点
//并且如果x不为叶子节点 那么现在所选取的叶子结点加上根节点刚好就为y*2
printf("%d\n",max(T[0].Query(x,y),T[1].Query(x,y)));//直径两段分别为根的情况取最大值
}
return 0;
}


