间断点

To Start

—— “间断点是啥？”
—— “间断点就是反映函数不连续的一些点。”

一、可去间断点

（1）定义

• $ \lim_{x \rightarrow x_0}存在，但是f(x)在x = x_0 的时候没有定义 $
• $ \lim_{x \rightarrow x_0}存在，且f(x)在x = x_0 的时候有定义，但是\lim_{x \rightarrow x_0}f(x) \neq f(x_0) $

（2）理解

可去间断点反映的是函数在某一个点的不连续性，但是这种不连续性可以通过重新定义函数值或者扩充定义域来消除。

可去间断点说明了在“瑕疵”点附近的函数变化趋势是相同的。

举一个比较通俗易懂的例子，如下图：

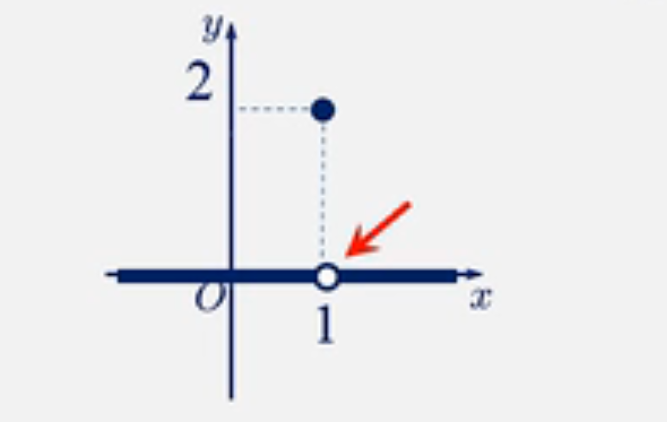
图中的x = 1就是这个函数的可去不间断点

（3）判断方法

• 找出函数的定义域，看是否有缺失的点，这些点可能是间断点。
• 对于每个缺失的点，求出函数在该点的左右极限，看是否都存在。
• 如果左右极限都存在，再看是否相等，如果相等，那么这个点就是可去间断点。
• 如果左右极限不相等或者至少有一个不存在，那么这个点就不是可去间断点。

二、跳跃间断点

（1）定义

• $ 如果 \lim_{x \rightarrow x_0^+} 和\lim_{x \rightarrow x_0^-}都存在，但是\lim_{x \rightarrow x_0^+} \neq \lim_{x \rightarrow x_0^-} ，就说x = x_0是f(x) 的跳跃间断点，并且此时不关注f(x_0)是否有定义$

（2）理解

其实这个非常好理解。反映的是不连续函数的断点。而且函数的不连续性不能通过重新定义函数值或者扩充定义域来清除。如图\(x = x_0\) 就是函数的跳跃间断点：

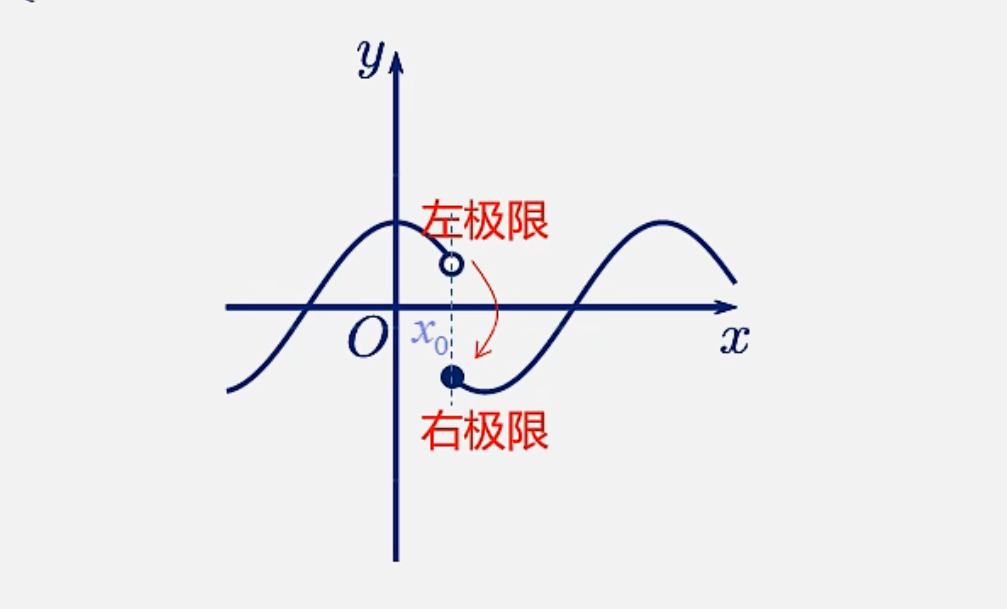
（3）判断方法

和上面的判断方法相似，就是判断两侧极限是不是存在，如果存在就看两个极限是不是相等，如果不相等那就是跳跃间断点。

三、无穷间断点

（1）定义

• \(就是x \rightarrow x_0 时，函数值趋近于无穷\)

（2）理解

只可意会不能言传

图中的 x=0 就是函数的无穷间断点

四、震荡间断点

（1）定义

• $ 当x \rightarrow x_0 时，函数值趋于震荡，并且不存在极限，那么x=x_0 就是函数的震荡间断点 $

（2）理解

如图是\(f(x) = xsin(\frac{1}{x})\)的图像

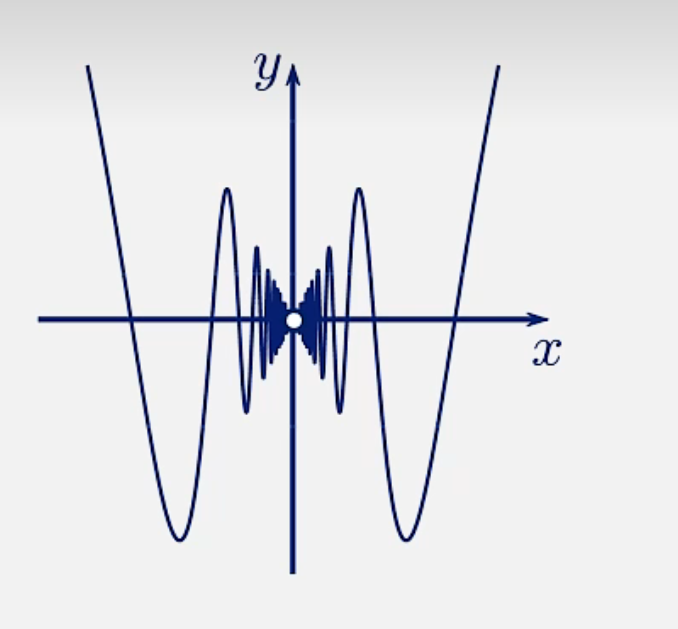
（3）判断方法

就看\(x \rightarrow x_0\)时，函数是否有极限。没有极限那大概率就是震荡间断点