【论文阅读】Safe Trajectory Generation for Complex Urban Environments Using Spatio-Temporal Semantic Corridor
有一篇可以参考的https://blog.csdn.net/u011841848/article/details/123173791
这篇文章代码在https://github.com/HKUST-Aerial-Robotics/spatiotemporal_semantic_corridor,有空要复现一下。
摘要:先定义什么叫语义元素(semantic elements):比如动态agents,交通信号灯,速度限制等等。这些语义元素有不同的数学表述(障碍物、约束、损失函数)。怎么统一调节这些不同元素的影响呢?这篇文章用了一个统一的时空语义走廊(SSC),是不同种类的语义元素的统一抽象表达。这样子的话碰撞检测这个非凸约束就变成了凸约束,轨迹生成变成了二次规划。且可以保证安全性和可行性,因为使用了凸包和贝塞尔曲线。
1. introduction
语义元素有不同的数学表述(障碍物、约束、损失函数)。所以用统一的形式表示不同的语义元素的影响很重要。
此外,怎么保证轨迹的安全性和可行性也是比较重要的问题。现在的方法,基于优化的和基于Lattice的,是在一系列采样点上检查约束,但采样点中间的轨迹段不一定成立了,所以不能保证整个轨迹的可行性。【好像一般不会,但可以考虑一下采样时间过长的场景,以及龙格现象的影响,这种问题确实存在,会影响控制】
以上两个问题,催生了这篇文章。关键点在于定义时空语义走廊SSC。怎么想到要定义这个SSC呢?是基于一个事实:大部分语义元素都可以被表示为两种形式之一:①时空障碍物 ②时空域上的区间范围。本质上,SSC是由一系列互相连接的无碰撞的cubes(包含动力学约束)组成的。定义了SSC之后,变成凸约束了,就可以用QP+贝塞尔曲线来解决。The proposed formulation is built on the top of the convex hull and hodograph properties of the Bézier curve.
文章的贡献对应了刚刚提的问题:① 语义元素统一的表达形式;②基于优化的轨迹生成,保证整个轨迹的安全和可行;③仿真平台,验证表现。
文章如何组织:II.相关工作, III,轨迹生成框架概览; IV,预备知识;V&VI,详细讲SSC和轨迹生成方法。VII实验。VIII结论。
2. related works
2.1 时空联合运动规划
时空运动规划有很多文章。[5]对时空lattice采样,用搜索方法获得可执行轨迹。[6]也是ST lattice,用数值优化方法可以符合车道几何线型。由于时空范围内维度太高,维度灾难,[6]用了GPU加速的动态规划。但上面这些文章不考虑其他语义元素(限速、信号灯)。
有的方法考虑了。一个朴素的想法是在损失函数里考虑这些限制。[9]用人工势能场APF,把这些元素整合在损失函数里面考虑,但缺点是局部最优。然而,损失函数里考虑,各项的权重难以权衡。[10]吧信号灯和动态障碍物作为S-T(纵向和时间)图像中的障碍物,然后搜索方法得结果。[1]把车道限制整合到障碍物里面,速度限制作约束条件。
基于上述的 obstacle-like和constraint-like的表示,本文提出了SSC,为轨迹优化提供信息。
2.2 行车走廊(也有译作行车隧道)的生成
空间上的行车走廊(自由行驶的凸空间)已经广泛运用了。[11]在初始路径附近生成无碰撞的“tube”,化运动规划问题为凸约束下的二次规划。[13]在参考轨迹附近找到一个凸的可行集(这个没太理解,是不是可行轨迹簇集合?)来加速非凸的优化,但计算复杂度还是高。此外,这些方法只考虑避碰,不考虑其他语义元素。
本文受空间行车走廊启发,拓展到时间-空间域,成为时空行车走廊SSC,且考虑了多种语义元素。
3. 系统概览
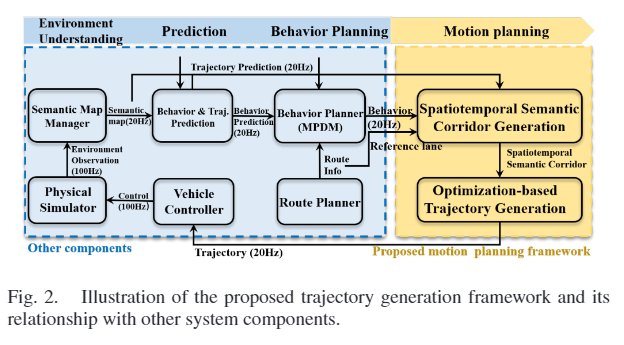
先明确,本方法属于运动规划层,因此需要上游模块(行为决策层)的结果作为输入。
一个规划循环(包含上游模块)有4个阶段:
①语义级地图信息。理解上就是把感知到的信息,用OGM、动态对象、交通规则等形式作表述,重构环境。
②预测。不仅要预测其他车的高级的驾驶行为,还要预测轨迹。
③行为决策。multi-policy decision making(MPDM),IV里面会提。
④运动规划。将行为决策给出的未来的离散的模拟得到的状态(应该就是粗略轨迹),作为行车隧道生成的种子点。注意,这个规划器可以承接任意可以给出未来状态的初始推测(初始概略轨迹)的行为决策器。
小总结一下,4个关键点:语义地图,他车预测轨迹,未来模拟状态(行为决策输出概略轨迹),全局规划给的参考车道。注意:若行为决策直接考虑了他车的预测状态,则预测模块可略去,他车的模拟状态当做轨迹。
文章还强调了一点,他们行为决策用了MPDM,其实已经考虑了他车的状态,但为了普适性,他们在实验里还是选用了预测的轨迹,所以可能会丢失交互信息。个人认为,如果把预测和决策一体化去考虑,加一些博弈的理论,再套进来,将会绝杀,以后可以研究研究。
4. multi-policy decision making的预备知识
MPDM把行为决策,视作一个 多智能体部分可观测的马尔科夫决策过程multi-agent partially observable Markov decision process (POMDP), 可以考虑交互和不确定性。
因为车数量增多时,解POMDP计算量上不可接受,MPDM把问题松弛,假设自车和他车都执行有限的离散“策略”集合,比如{换道,保持车道等(说叫策略policy,其实应该叫意图maneuver/intention)}。然后每个闭环的“策略”又可以用简化的仿真模型,前向模拟生成未来的预测状态,比如理想化的转角和速度控制器。【也就是说,还是对抽象的高级驾驶行为做决策,再辅以一个简单规划器搞一个粗略轨迹】
本文用前向模拟生成的模拟状态作为种子点,生成走廊。需要说明的是:这些初始种子点不会碰撞,但不能直接执行,因为时间粒度粗糙并且模拟模型很简化。
MPDM一次性可以提供多种maneuver的未来模拟状态,本文充分利用这个特性,一次性为所有可能的maneuver生成对应的轨迹候选集,来增强稳定性。
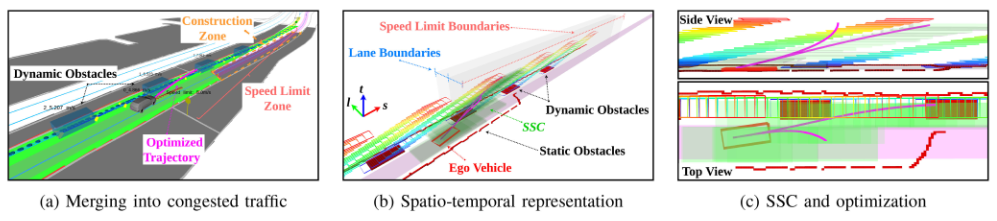
5.时空Corridor
5.1 语义元素和frenet坐标
构型空间:S-L-T。结合Frenet坐标系,比较好理解,不多说了。
语义元素分两类:obstacle-like和constraint-like
①obstacle-like
物理意义为:slt空间上不允许行驶的一个特定部分。动静态障碍物都是。红灯视作一定时期占据特定纵向位置的障碍物。构型空间表达为一个3D Occupancy Grid
②constraint-like
特指一些动力学约束或时域上的约束。限速以及停车线可以视作速度约束。时间上的约束有点不理解,举了一个例子说,换道的时候,换道总时长不应该过长。为了整合constraint-like约束,文章提出一个统一的表述叫做语义边界(semantic boundaries)。比如限速,可以视作[s_begin,s_end]上的速度约束,s_begin和s_end就是两个语义边界。换道过程,可以视作[d_begin, d_end]上的时间约束,d_begin, d_end就是两个语义边界。注意约束层面有软约束和硬约束之分,下面会详细说。
5.2 Semantic Corridor Generation
①种子点生成
SSC的可行性取决于环境复杂度和种子点的优劣。首先要保证种子直接构成的立方体(fig 4.a,注意一下fig 4是S-T图像)无碰撞。
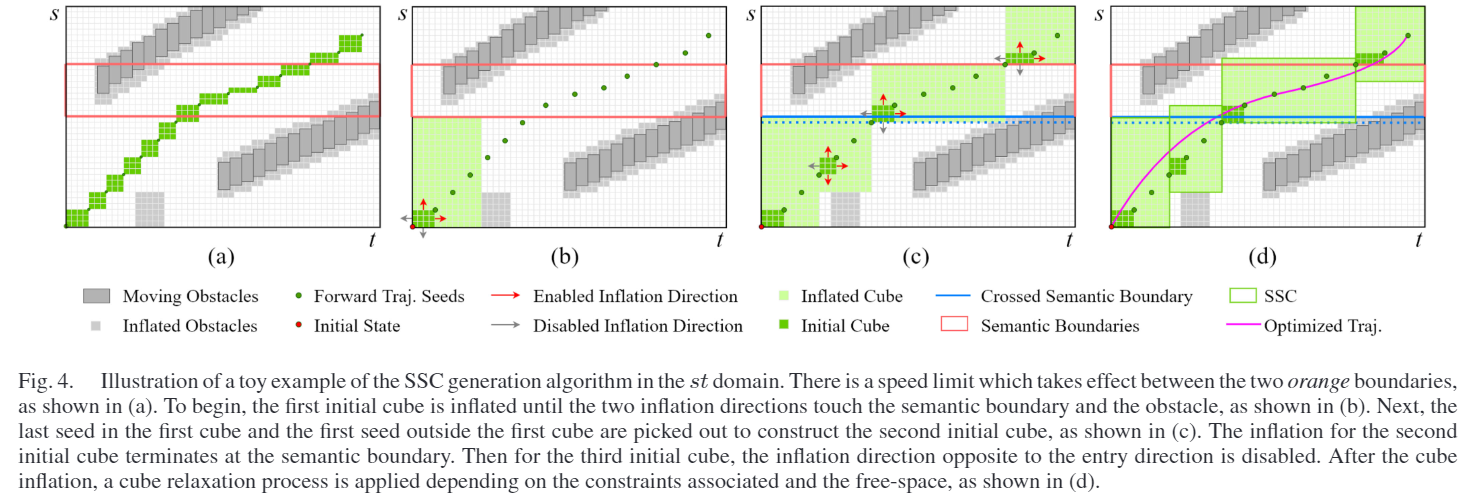
② 结合语义边界,膨胀立方体
基于种子点迭代生成走廊,上次膨胀后的立方体如果包含该种子点,则跳过。膨胀的对象是一系列初始立方体,是连续两个种子点作为顶点生成的。
膨胀过程中,务必注意考虑语义边界,这样就能考虑约束。具体来说,膨胀时碰到语义边界或者障碍物,这个维度就会停止膨胀。文中提到,为了保证凸性,不清晰地优化每一块cube的持续时间,当前cube的时间上界应该和下一个cube的时间下界刚好一致。如果想考虑改进这一点,可以增加时间维度的重叠。(这边不是很理解)

③ cube的松弛
一些软约束,用一定的裕度,允许其膨胀超界。
6.保障安全和可行的轨迹生成
文章先解释了为什么不用五次多项式?①一段五次多项式的表达能力非常弱,可能无法表达一个复杂约束下的maneuver ②这种多项式不适用于复杂构型空间和复杂动力学约束的问题,约束只在部分采样点上检查,两点间的可行性无法保证。文章在S和L两个维度上用了贝塞尔曲线。
6.1. 贝塞尔曲线基础和属性
m维的贝塞尔曲线是由m+1个控制点定义的。

凸包特性:贝塞尔曲线必然在控制点组成的凸包内。所以凸包都是自由空间的话,曲线也是无碰撞的。
速端曲线特性(不懂the hodograph property):约束曲线的高阶微分,可以用于动力学约束。基于这个特性,初始贝塞尔曲线的一阶导数也是贝塞尔曲线,控制点是 ![]() 。对这个一阶导数的贝塞尔曲线再应用凸包特性,可以保证动力学约束。
。对这个一阶导数的贝塞尔曲线再应用凸包特性,可以保证动力学约束。
6.2. 分段的贝塞尔曲线表示
轨迹是分段贝塞尔曲线,每段都与一个SSC的cube关联。
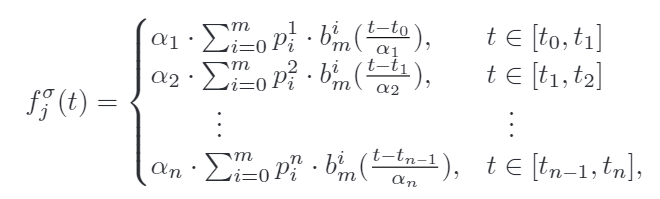
目标函数就是横向jerk和纵向jerk平方加权和,然后给变换到贝塞尔曲线能表达的形式。
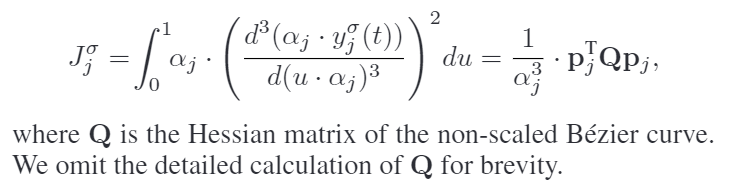
6.3 施加安全和动力学约束
文章用了五阶贝塞尔曲线。
由于 hodograph property,那么贝塞尔曲线的k阶微分,是位于以下这些控制点组成的凸包里面的:
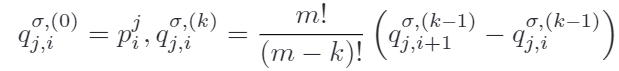
每一段贝塞尔曲线的k阶微分,在端点部分是被控制点约束的,两端约束为
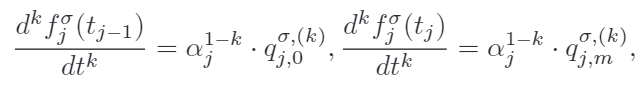
考虑语义元素约束时,k阶微分需要在一定区间内,实际上只要保证控制点不越界就可以了,因为有凸包性质
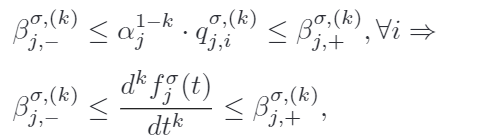
下面具体分析一下约束条件。
① 预期状态约束(说的玄乎玄乎的,就是整个轨迹的两端约束)
起点和终点是确定的,所以对第一段的起点和最后一段的终点需要明确,
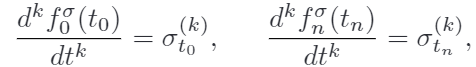
k=0,1,2,就是一直约束到二阶导。写成上面提到的两端约束形式。
② 连续性约束
因为是分段的贝塞尔曲线,在连接部分应该连续。
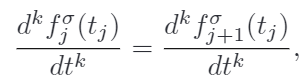
k=0,1,2,3,也就是说一直到3阶导数(jerk相关)都应该一样。还是写成两端约束形式。这个是每一段轨迹的两端约束。
③ 自由空间约束:
顾名思义就是无碰撞约束。有了每个cube的边界,只要把上面不等式约束写成0阶导形式就行。
④动力学约束
把上面不等式约束写成高阶导形式就行。
综上,模型建立完毕,这是一个二次规划问题,可以很快地用优化算法解决。
7.实验结果
貌似只有个定性的结果,但是确实这个如何定量呢?
不细说了
8.结论
主要贡献是2个:SSC和相应的贝塞尔轨迹生成方法。
主要的缺陷是:预测的不确定性和交互的不确定性没有被充分建模
词语积累
non-trivial
tune
enforce
render
the trajectory parameterization
hodograph
conform
facilitate
intractable
clearance
twofold
relax the problem
a space-time manifold
a quadratic programming (QP) formulation
There is extensive literature on





