2018-2019 9th BSUIR Open Programming Championship
I. Equal Mod Segments
\(1 \leq n \leq 1e5\)
\(1 \leq a_i \leq 3e5\)
题解:ST表 + 扫描线 + 二维偏序
取模存在一个不错的性质:\(x \%p\)要么\(x\)不变,要么\(x\)至少整除\(2\)
所以我们考虑固定左端点\(l\),存在\(log\ a_l\)段区间,使得右端点\(r\)在每段区间\([p,q]\)内\(a_l\ mod\ a_{l + 1}...mod\ a_r,r\in[p,q]\)不变
我们可以通过\(ST\)表+二分来预处理所有固定左端点和固定右端点的区间,并将所有模数相同的区间放入同一个\(vector\)中,预处理复杂度 \(O(nlog^2n)\)
那么我们考虑区间\([l,r]\)满足什么条件,才能对答案产生贡献
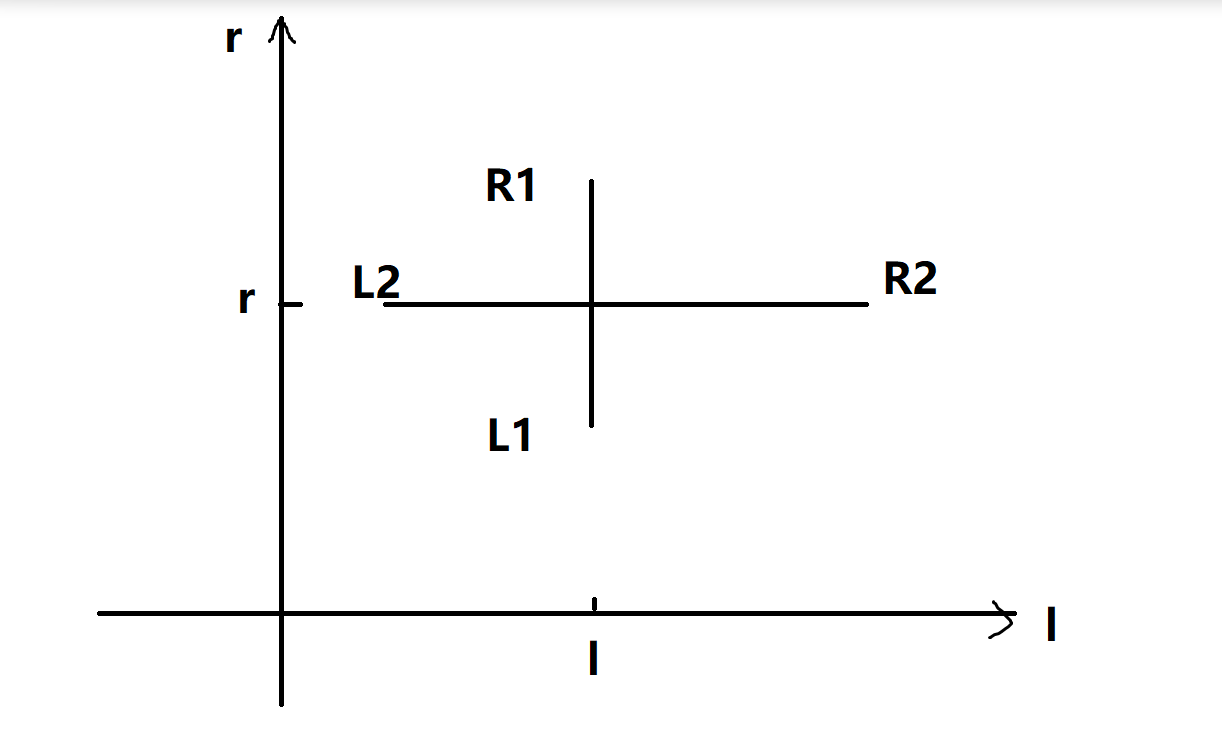
我们设对于\(l\)来说,模数为\(p\)的右端点\(r\)所在区间为\([L_1,R_1]\),对于\(r\)来说,模数为\(p\)的左端点\(l\)所在区间为\([L_2,R_2]\),那么只要保证\(L_1\leq r \leq R_1 \and L_2\leq l \leq R_2\),那么区间\([l,r]\)就能对答案产生贡献
我们把条件抽象到二维平面上,横坐标为\(l\),纵坐标为\(r\),可以得到:
- 所以我们只要对每个模数的\(vector\)跑一次扫描线即可,扫描\(x\)轴,线段树维护\(y\)轴,求交点数量即可
const int N = 3e5 + 10, M = 4e5 + 10;
int n, a[N], st[N][18], lg2[N];
vector<array<int, 4>> vec[N];
struct info
{
int sum;
friend info operator+(const info &a, const info &b)
{
info c;
c.sum = a.sum + b.sum;
return c;
}
};
struct SEG
{
info val;
} seg[N << 2];
void up(int id)
{
seg[id].val = seg[lson].val + seg[rson].val;
}
void change(int id, int l, int r, int x, int val)
{
if (l == r)
{
seg[id].val.sum += val;
return;
}
int mid = l + r >> 1;
if (x <= mid)
change(lson, l, mid, x, val);
else
change(rson, mid + 1, r, x, val);
up(id);
}
info query(int id, int l, int r, int ql, int qr)
{
if (ql <= l && r <= qr)
return seg[id].val;
int mid = l + r >> 1;
if (qr <= mid)
return query(lson, l, mid, ql, qr);
else if (ql > mid)
return query(rson, mid + 1, r, ql, qr);
else
return query(lson, l, mid, ql, qr) + query(rson, mid + 1, r, ql, qr);
}
void build()
{
for (int i = 1; i <= n; ++i)
st[i][0] = a[i];
for (int i = 2; i <= n; ++i)
lg2[i] = lg2[i >> 1] + 1;
for (int j = 1; j <= 15; ++j)
for (int i = 1; i + (1ll << j) - 1 <= n; ++i)
st[i][j] = min(st[i][j - 1], st[i + (1ll << (j - 1))][j - 1]);
}
int query(int l, int r)
{
if (l > r)
return INF;
int len = lg2[r - l + 1];
return min(st[l][len], st[r - (1ll << len) + 1][len]);
}
void solve()
{
cin >> n;
int m = 0;
for (int i = 1; i <= n; ++i)
{
cin >> a[i];
m = max(m, a[i]);
}
build();
for (int i = 1; i <= n; ++i)
{
int now = a[i];
for (int j = i, l, r; j <= n; j = r + 1)
{
l = j, r = n;
while (l <= r)
{
int mid = l + r >> 1;
if (query(j + 1, mid) > now)
l = mid + 1;
else
r = mid - 1;
}
vec[now].push_back({0, i, j, r});
if (r + 1 <= n)
now %= a[r + 1];
}
}
for (int i = n; i >= 1; --i)
{
int now = a[i];
for (int j = i, l, r; j >= 1; j = l - 1)
{
l = 1, r = j;
while (l <= r)
{
int mid = l + r >> 1;
if (query(mid, j - 1) > now)
r = mid - 1;
else
l = mid + 1;
}
vec[now].push_back({1, i, l, j});
if (l - 1 >= 1)
now %= a[l - 1];
}
}
int ans = 0;
for (int i = 0; i <= m; ++i)
{
if (vec[i].empty())
continue;
vector<array<int, 4>> evt;
for (auto [op, k, l, r] : vec[i])
{
if (op == 0) // 查询
evt.push_back({k, 0, l, r});
else
{
evt.push_back({l, -1, k, 1}); // 添加贡献
evt.push_back({r, 1, k, -1}); // 删除贡献
}
}
// 扫描线
sort(all(evt));
for (auto [y, op, l, r] : evt)
{
if (op == 0)
ans += query(1, 1, n, l, r).sum;
else
change(1, 1, n, l, r);
}
}
cout << ans << endl;
}
K. Innovations
题解:树链剖分 + 势能线段树
- 考虑到根号的性质,所以显然势能线段树维护\(dfs\)序
- 我们考虑每条边对答案产生的贡献为\(sz[v] \times (n - sz[v]),sz[v]为v的子树大小\)
- 设边权为\(w[v]\),每条边的贡献为\(p[v]\),那么每条边对答案的贡献为\(w[v] \times p[v]\),所以我们线段树直接维护答案,如果该区间不全为\(1\)就暴力递归到叶子节点进行修改
const int N = 2e5 + 10;
const int mod = 1e9 + 7;
int n, m, sz[N], p[N], dep[N], top[N], hson[N], l[N], r[N], fa[N], w[N], idx, mp[N];
vector<pair<int, int>> g[N];
void dfs1(int u, int par)
{
fa[u] = par;
dep[u] = dep[par] + 1;
sz[u] = 1;
hson[u] = -1;
for (auto [v, val] : g[u])
{
if (v == par)
continue;
dfs1(v, u);
sz[u] += sz[v];
w[v] = val;
p[v] = sz[v] * (n - sz[v]);
if (hson[u] == -1 || sz[v] > sz[hson[u]])
hson[u] = v;
}
}
void dfs2(int u, int head)
{
top[u] = head;
l[u] = ++idx;
mp[idx] = u;
if (hson[u] != -1)
dfs2(hson[u], head);
for (auto [v, val] : g[u])
{
if (v == fa[u])
continue;
if (v == hson[u])
continue;
dfs2(v, v);
}
r[u] = idx;
}
struct info
{
int sum, flag; // flag 代表区间是否全为 1
friend info operator+(const info &a, const info &b)
{
info c;
c.sum = (a.sum + b.sum) % mod;
c.flag = a.flag && b.flag;
return c;
}
info(int sum = 0, int flag = 0) : sum(sum), flag(flag) {}
};
struct SEG
{
int lazy;
info val;
} seg[N << 2];
void up(int id)
{
seg[id].val = seg[lson].val + seg[rson].val;
}
void build(int id, int l, int r)
{
if (l == r)
{
if (mp[l] == 1)
{
seg[id].val = info(0, 1);
return;
}
if (w[mp[l]] == 1)
seg[id].val = info(w[mp[l]] * p[mp[l]], 1);
else
seg[id].val = info(w[mp[l]] * p[mp[l]], 0);
return;
}
int mid = l + r >> 1;
build(lson, l, mid);
build(rson, mid + 1, r);
up(id);
}
void modify(int id, int l, int r, int ql, int qr)
{
if (ql <= l && r <= qr && seg[id].val.flag)
return;
if (l == r)
{
w[mp[l]] = (int)(sqrt(w[mp[l]]));
if (w[mp[l]] == 1)
seg[id].val.flag = 1;
else
seg[id].val.flag = 0;
seg[id].val.sum = w[mp[l]] * p[mp[l]];
return;
}
int mid = l + r >> 1;
if (qr <= mid)
modify(lson, l, mid, ql, qr);
else if (ql > mid)
modify(rson, mid + 1, r, ql, qr);
else
{
modify(lson, l, mid, ql, qr);
modify(rson, mid + 1, r, ql, qr);
}
up(id);
}
void solve()
{
cin >> n >> m;
for (int i = 1; i < n; ++i)
{
int u, v, w;
cin >> u >> v >> w;
g[u].push_back({v, w});
g[v].push_back({u, w});
}
dfs1(1, 0);
dfs2(1, 1);
build(1, 1, n);
cout << seg[1].val.sum << endl;
while (m--)
{
int u, v;
cin >> u >> v;
while (top[u] != top[v])
{
if (dep[top[u]] > dep[top[v]])
{
modify(1, 1, n, l[top[u]], l[u]);
u = fa[top[u]];
}
else
{
modify(1, 1, n, l[top[v]], l[v]);
v = fa[top[v]];
}
}
if (dep[u] > dep[v] && l[v] + 1 <= l[u])
modify(1, 1, n, l[v] + 1, l[u]);
else if (dep[u] < dep[v] && l[u] + 1 <= l[v])
modify(1, 1, n, l[u] + 1, l[v]);
cout << seg[1].val.sum << endl;
}
}