2019 ICPC Universidad Nacional de Colombia Programming Contest
A. Amazon
给定\(n\)条直线(存在共线的情况),在每两条垂直的直线的交点处需要建一个交叉点,求交叉点的数量,注意需要去除共线时候的交叉点
题解
因为要除去共线的情况,我们考虑将一条直线以方向向量\(v\),与\(x\)轴的交点的横坐标\(x\)的方式存储
注意:
对于\(v\)来说需要最简形式,并且我们需要保证向量的方向尽可能指向\(y\)轴右侧,因为方向向量\((-1,0)\)和\((1, 0)\)实际上一样的,但是我们不关注向量的方向,那么很有可能两条共线的直线会被当成两条不一样的直线
对于\(x\)来说,我们需要用一个\(pair\)去存储分子和分母,因为直接求出\(x\)的话存在精度误差,注意特判平行\(x\)轴的情况
我们通过\(map\)记录每个向量的出现次数
那么对于一条直线的方向向量\(v\)来说,怎么判断与该向量垂直的向量是什么呢?
我们考虑将\(v\)逆时针旋转\(90°\)得到向量\(v'\)
- 那么答案显然为
\[ \frac{\sum_v mp[v']}{2} \]
const int N = 2e5 + 10, M = 4e5 + 10;
using point_type = long long;
// 点与向量
template <typename T>
struct point
{
T x, y;
bool operator==(const point &a) const
{
return (fabs(x - a.x) <= eps && fabs(y - a.y) <= eps);
}
bool operator<(const point &a) const
{
if (fabs(x - a.x) <= eps)
return y < a.y - eps;
return x < a.x - eps;
}
bool operator>(const point &a) const
{
return !(*this < a || *this == a);
}
point operator+(const point &a) const
{
return {x + a.x, y + a.y};
}
point operator-(const point &a) const
{
return {x - a.x, y - a.y};
}
point operator-() const
{
return {-x, -y};
}
point operator*(const T k) const
{
return {k * x, k * y};
}
point operator/(const T k) const
{
return {x / k, y / k};
}
// 点积
T operator*(const point &a) const
{
return x * a.x + y * a.y;
}
// 叉积
T operator^(const point &a) const
{
return x * a.y - y * a.x;
}
// to_left 测试
int to_left(const point &a) const
{
auto t = (*this) ^ a;
return (t > eps) - (t < -eps);
}
// 模长的平方
T quad_len() const
{
return (*this) * (*this);
}
// 两点距离的平方
T quad_dis(const point &a) const
{
return (a - (*this)).quad_len();
}
// 向量模长
long double len() const
{
return sqrtl(quad_len());
}
// 两点距离
long double dis(const point &a) const
{
return sqrtl(quad_dis(a));
}
// 向量逆时针旋转
point rotate(const long double rad) const
{
return {x * cos(rad) - y * sin(rad), x * sin(rad) + y * cos(rad)};
}
void reduce()
{
int d = gcd(x, y);
x /= d, y /= d;
bool flag = false;
if (x < 0)
{
flag ^= 1;
x = -x;
}
if (y < 0)
{
flag ^= 1;
y = -y;
}
if (flag)
x = -x;
if (y == 0)
x = abs(x);
}
};
using Point = point<point_type>;
pair<int, int> reduce(pair<int, int> a)
{
auto [x, y] = a;
int d = gcd(x, y);
x /= d, y /= d;
bool flag = false;
if (x < 0)
{
flag ^= 1;
x = -x;
}
if (y < 0)
{
flag ^= 1;
y = -y;
}
if (flag)
x = -x;
return {x, y};
}
int n;
void solve()
{
cin >> n;
vector<pair<Point, pair<int, int>>> vec;
for (int i = 1; i <= n; ++i)
{
int x1, y1, x2, y2;
cin >> x1 >> y1 >> x2 >> y2;
Point a = {x1, y1}, b = {x2, y2}, v = {x2 - x1, y2 - y1};
v.reduce();
if (y1 == y2)
{
pair<int, int> p = {y1, y1};
vec.push_back({v, p});
continue;
}
pair<int, int> p = {(x2 - x1) * y1 + x1 * (y1 - y2), y1 - y2};
p = reduce(p);
vec.push_back({v, p});
}
sort(all(vec));
vec.erase(unique(all(vec)), vec.end());
map<Point, int> mp;
for (auto [p, it] : vec)
mp[p]++;
int ans = 0;
for (auto [p, it] : vec)
{
Point rev = {-p.y, p.x};
rev.reduce();
if (mp.count(rev))
ans += mp[rev];
}
cout << ans / 2 << endl;
}
D. Do Not Try This Problem
\(1 \leq n,q \leq 1e5\)
题解
我们考虑离线,考虑倒序操作,因为倒着操作的话,只要一个位置被修改了,那么该位置永远不会被修改
我们考虑公差\(a\):
- 若\(a > \sqrt{n}\):
我们考虑直接暴力修改,复杂度\(O(n\sqrt{n})\)
- 若\(a \leq \sqrt{n}\):
我们考虑对每一个公差\(a\)开一个并查集,对于每次操作直接合并\(i, i + a,...i+ka\)这些位置,所以说由于起始位置\(i\)不同,所以对于每个并查集来说,最多遍历\(n\)个位置,因为有\(\sqrt{n}\)个并查集,所以复杂度为\(n\sqrt{n}\)
过程中我们开个\(vis\),记录某个位置有没有修改即可
const int N = 1e5 + 10, M = 4e5 + 10, B = 330;
int n, q, vis[N]; // vis[i] 代表第i个位置有没有被修改过
struct DSU
{
int fa[N];
void clear()
{
for (int i = 1; i <= n; ++i)
fa[i] = i;
}
int find(int x)
{
return x == fa[x] ? x : fa[x] = find(fa[x]);
}
void merge(int x, int y)
{
int fx = find(x), fy = find(y);
if (fx != fy)
fa[fx] = fy;
}
} dsu[B];
struct Qry
{
int pos, d, k;
char ch;
} qry[N];
void solve()
{
string s;
cin >> s;
n = s.length();
s = " " + s;
int m = sqrt(n) + 1;
for (int i = 1; i <= m; ++i)
dsu[i].clear();
cin >> q;
for (int i = 1; i <= q; ++i)
{
int pos, d, k;
char ch;
cin >> pos >> d >> k >> ch;
qry[i] = {pos, d, k, ch};
}
for (int i = q; i >= 1; --i)
{
auto [pos, d, k, ch] = qry[i]; // 起始位置 pos,公差 d,项数 k,修改后的字符 ch
if (d >= m)
{
for (int j = pos; j <= pos + k * d; j += d)
{
if (!vis[j])
{
vis[j] = true;
s[j] = ch;
}
}
}
else
{
for (int j = dsu[d].find(pos); j <= pos + k * d; j = dsu[d].find(j))
{
if (!vis[j])
{
vis[j] = true;
s[j] = ch;
}
if (j == pos + k * d)
break;
dsu[d].merge(j, j + d);
}
}
}
cout << s.substr(1) << endl;
}
E. Extreme Image
给定一个扇形的一部分,角度为\(\alpha\),长度为\(d\),以及平面上\(n\)个点的极坐标\((w,r)\),求该扇形最多能覆盖多少个点
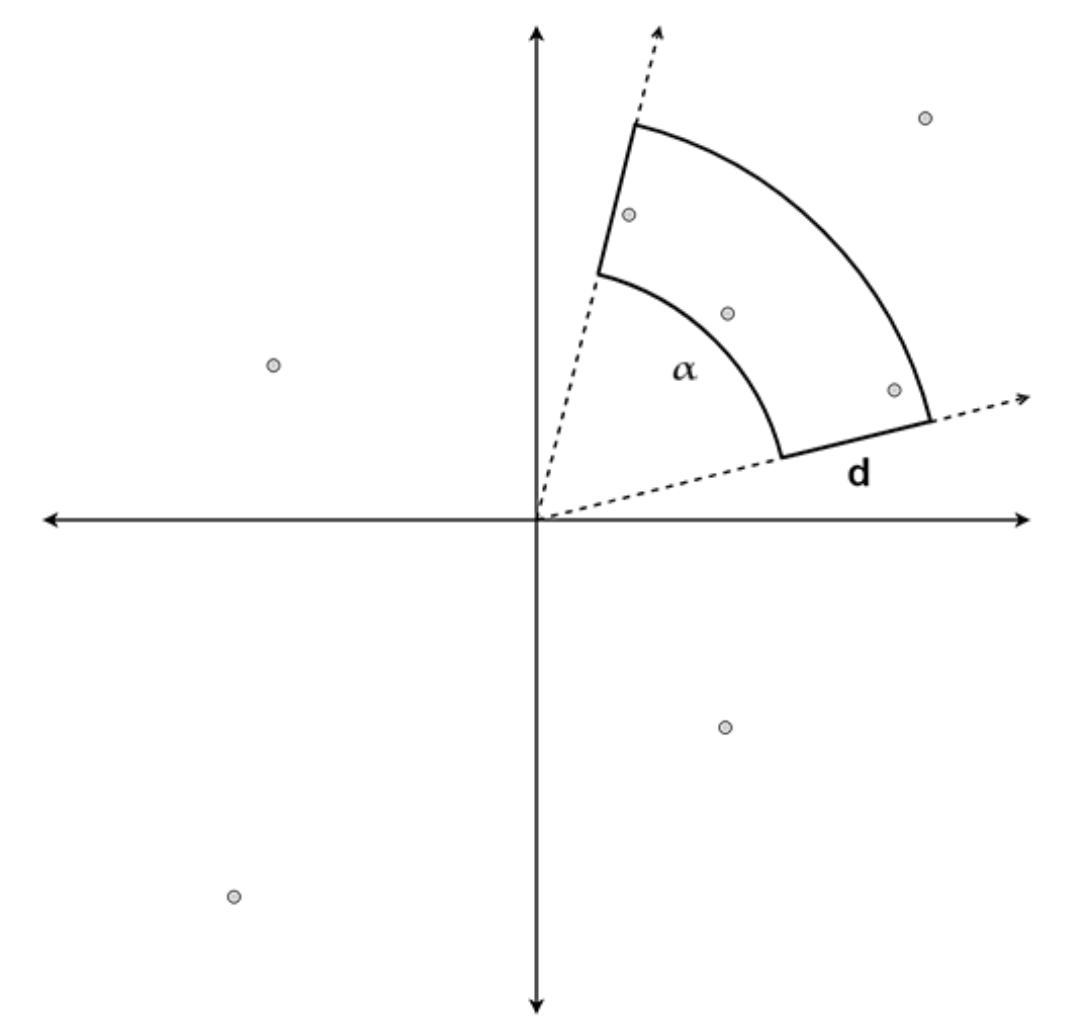
\(1 \leq d,r \leq 1e5\)
\(0 \leq \alpha,w < 360.00,存在两位小数\)
题解:扫描线 + 线段树
- 经典问题,考虑每个点能在什么时候产生贡献
- 显然对于一个点\((w, r)\)来说,只要扇形的左上角在\(([w,w+\alpha], [r,r + d])\)这些区域内,那么该点就能产生贡献,所以只要在\(w\)和\(w + \alpha\)两个位置设置事件即可
- 对于一个扇形来说存在上边和下边,我们钦定上边遇到\(w\)时贡献\(+1\),上边遇到\(w + \alpha\)时贡献\(-1\)
- 我们钦定上边从\(0\)开始扫描,所以我们需要提前将\([360°-\alpha,360°]\)的事件点加入线段树中,那么当上边从\(0\)扫描至\(360\),就考虑了所有情况
- 注意该题角度为实数,我们考虑将角度乘上\(1000\),为什么不乘\(100\)?,因为存在精度问题
const int N = 2e5 + 10, M = 4e5 + 10;
int n, d, w[N], r[N];
double len;
vector<array<int, 4>> evt;
struct info
{
int mx;
friend info operator+(const info &a, const info &b)
{
info c;
c.mx = max(a.mx, b.mx);
return c;
}
};
struct SEG
{
int lazy;
info val;
} seg[N << 2];
void up(int id)
{
seg[id].val = seg[lson].val + seg[rson].val;
}
void settag(int id, int tag)
{
seg[id].val.mx += tag;
seg[id].lazy += tag;
}
void down(int id)
{
if (seg[id].lazy == 0)
return;
settag(lson, seg[id].lazy);
settag(rson, seg[id].lazy);
seg[id].lazy = 0;
}
void modify(int id, int l, int r, int ql, int qr, int val)
{
if (ql <= l && r <= qr)
{
settag(id, val);
return;
}
down(id);
int mid = l + r >> 1;
if (qr <= mid)
modify(lson, l, mid, ql, qr, val);
else if (ql > mid)
modify(rson, mid + 1, r, ql, qr, val);
else
{
modify(lson, l, mid, ql, qr, val);
modify(rson, mid + 1, r, ql, qr, val);
}
up(id);
}
void solve()
{
cin >> n >> d >> len;
int alpha = (int)(len * 1000);
for (int i = 1; i <= n; ++i)
{
cin >> r[i];
double x;
cin >> x;
w[i] = (int)(x * 1000);
}
int m = 2e5 + 10;
for (int i = 1; i <= n; ++i)
{
int L = w[i], R = w[i] + alpha;
int ql = r[i], qr = r[i] + d;
if (R >= 360000)
R %= 360000;
evt.push_back({R, 1, ql, qr});
// 提前加入线段树
if (L <= 360000 && L >= 360000 - alpha)
modify(1, 1, m, ql, qr, 1);
evt.push_back({L, -1, ql, qr});
}
// 扫描线
sort(all(evt));
int ans = seg[1].val.mx;
for (auto [k, op, l, r] : evt)
{
if (op == -1)
modify(1, 1, m, l, r, 1);
else
modify(1, 1, m, l, r, -1);
ans = max(ans, seg[1].val.mx);
}
cout << ans << endl;
}
F. Fraction Formula
题解
- 经典表达式求值问题,用栈维护即可
- 注意在分式化简时必定爆\(long\ long\),考虑先求\(lcm\)后再求\(gcd\)进行化简
const int N = 4e5 + 10;
typedef pair<int, int> pii;
pii reduce(pii tmp)
{
auto [a, b] = tmp;
bool flag = false;
if (a < 0)
{
flag ^= 1;
a = -a;
}
if (b < 0)
{
flag ^= 1;
b = -b;
}
int d = gcd(a, b);
a /= d, b /= d;
if (flag)
a = -a;
return {a, b};
}
pii operator+(const pii &t1, const pii &t2)
{
auto [b1, a1] = t1;
auto [b2, a2] = t2;
pii c;
int lc = lcm(a1, a2);
c.second = lc;
c.first = b1 * (lc / a1) + b2 * (lc / a2);
return reduce(c);
}
pii operator-(const pii &t1, const pii &t2)
{
auto [b1, a1] = t1;
auto [b2, a2] = t2;
pii c;
int lc = lcm(a1, a2);
c.second = lc;
c.first = b1 * (lc / a1) - b2 * (lc / a2);
return reduce(c);
}
pii fac[N];
int idx;
void solve()
{
string s;
while (cin >> s)
{
idx = 0;
s = "(" + s;
s += ")";
int n = s.length();
s = " " + s;
stack<pii> stk;
for (int i = 1; i <= n; ++i)
{
if (s[i] == '(')
stk.push({i, 0});
else if (s[i] == '/')
{
int a = 0, b = 0;
int pos = i - 1, p = 1;
while (isdigit(s[pos]))
{
a = (s[pos] - '0') * p + a;
p *= 10;
pos--;
}
pos = i + 1;
while (isdigit(s[pos]))
{
b = b * 10 + (s[pos] - '0');
pos++;
}
fac[++idx] = reduce({a, b});
stk.push({idx, 1});
}
else if (s[i] == ')')
{
vector<pii> vec;
while (stk.size())
{
if (stk.top().second == 0 && s[stk.top().first] == '(')
{
stk.pop();
break;
}
vec.push_back(stk.top());
stk.pop();
}
reverse(all(vec));
pii res = fac[vec.front().first];
// cerr << res.first << "/" << res.second << endl;
for (int i = 1; i < vec.size(); ++i)
{
auto [id, op] = vec[i];
if (op == 0 && s[id] == '+')
res = res + fac[vec[i + 1].first];
else if (op == 0 && s[id] == '-')
res = res - fac[vec[i + 1].first];
}
fac[++idx] = res;
stk.push({idx, 1});
}
else if (s[i] == '+' || s[i] == '-')
stk.push({i, 0});
}
cout << fac[idx].first << "/" << fac[idx].second << endl;
}
}
J. Jail Destruction
对于一个环形的序列,存在两个操作:
- \(Modify:[l,r],a_i:=max(0,a_i - x)\)
- \(Query:\sum_{i = l}^r a_i\)
\(1 \leq n,q\leq 1e5\)

题解
解法\(1\):
考虑线段树上维护:区间非\(0\)数的最小值\(mi,mi>0\),区间非\(0\)元素的个数\(len\),区间和\(sum\)
考虑区间修改操作:
若\(sum=0\),直接退出
若\(x < mi\),\(sum:=sum - len * x;mi:=mi - x\),显然\(len\)不用改变,并且修改后区间信息正确,并打上懒惰标记
若\(x \geq mi\),我们考虑暴力递归
解法\(2\):
- 容易发现第一个操作可以拆成两个操作:区间加和区间对\(0\)取\(min\)
- 显然\(Segment \ beats\)板子题
const int N = 1e5 + 10;
int n, q, a[N];
struct info
{
int mi, len, sum;
friend info operator+(const info &a, const info &b)
{
info c;
c.mi = min(a.mi, b.mi);
c.len = a.len + b.len;
c.sum = a.sum + b.sum;
return c;
}
info(int mi = 0, int len = 0, int sum = 0) : mi(mi), len(len), sum(sum) {}
};
struct SEG
{
int lazy;
info val;
} seg[N << 2];
void up(int id)
{
seg[id].val = seg[lson].val + seg[rson].val;
}
void build(int id, int l, int r)
{
if (l == r)
{
seg[id].val = info(a[l], 1, a[l]);
return;
}
int mid = l + r >> 1;
build(lson, l, mid);
build(rson, mid + 1, r);
up(id);
}
void settag(int id, int tag)
{
auto [mi, len, sum] = seg[id].val;
seg[id].val.sum -= len * tag;
seg[id].val.mi -= tag;
seg[id].lazy += tag;
}
void down(int id)
{
if (seg[id].lazy == 0)
return;
settag(lson, seg[id].lazy);
settag(rson, seg[id].lazy);
seg[id].lazy = 0;
}
void modify(int id, int l, int r, int ql, int qr, int x)
{
if (seg[id].val.sum == 0)
return;
if (ql <= l && r <= qr && x < seg[id].val.mi)
{
settag(id, x);
return;
}
if (l == r)
{
seg[id].val.sum = max(0ll, seg[id].val.sum - x);
seg[id].val.len = (seg[id].val.sum == 0 ? 0 : 1);
seg[id].val.mi = (seg[id].val.sum == 0 ? INF : seg[id].val.mi);
return;
}
down(id);
int mid = l + r >> 1;
if (qr <= mid)
modify(lson, l, mid, ql, qr, x);
else if (ql > mid)
modify(rson, mid + 1, r, ql, qr, x);
else
{
modify(lson, l, mid, ql, qr, x);
modify(rson, mid + 1, r, ql, qr, x);
}
up(id);
}
info query(int id, int l, int r, int ql, int qr)
{
if (ql <= l && r <= qr)
{
return seg[id].val;
}
down(id);
int mid = l + r >> 1;
if (qr <= mid)
return query(lson, l, mid, ql, qr);
else if (ql > mid)
return query(rson, mid + 1, r, ql, qr);
else
return query(lson, l, mid, ql, qr) + query(rson, mid + 1, r, ql, qr);
}
void solve()
{
cin >> n >> q;
for (int i = 1; i <= n; ++i)
cin >> a[i];
build(1, 1, n);
while (q--)
{
int op, l, r, x;
cin >> op >> l >> r;
if (op == 1)
{
if (l <= r)
cout << query(1, 1, n, l, r).sum << endl;
else
cout << query(1, 1, n, l, n).sum + query(1, 1, n, 1, r).sum << endl;
}
else
{
cin >> x;
if (l <= r)
modify(1, 1, n, l, r, x);
else
{
modify(1, 1, n, l, n, x);
modify(1, 1, n, 1, r, x);
}
}
}
}
const int N = 1e5 + 10;
int n, q, a[N];
struct info
{
int mi, sc, cnt, sum, len;
friend info operator+(const info &a, const info &b)
{
info c;
if (a.mi == b.mi)
{
c.mi = a.mi;
c.cnt = a.cnt + b.cnt;
c.sc = min(a.sc, b.sc);
}
else if (a.mi < b.mi)
{
c.mi = a.mi;
c.cnt = a.cnt;
c.sc = min(a.sc, b.mi);
}
else
{
c.mi = b.mi;
c.cnt = b.cnt;
c.sc = min(a.mi, b.sc);
}
c.sum = a.sum + b.sum;
c.len = a.len + b.len;
return c;
}
info(int mi = 0, int sc = 0, int cnt = 0, int sum = 0, int len = 0) : mi(mi), sc(sc), cnt(cnt), sum(sum), len(len) {}
};
struct SEG
{
int lazy_add, lazy_mx;
info val;
} seg[N << 2];
void up(int id)
{
seg[id].val = seg[lson].val + seg[rson].val;
}
void build(int id, int l, int r)
{
seg[id].lazy_add = 0, seg[id].lazy_mx = -1;
if (l == r)
{
seg[id].val = info(a[l], INF, 1, a[l], 1);
return;
}
int mid = l + r >> 1;
build(lson, l, mid);
build(rson, mid + 1, r);
up(id);
}
void settag_mx(int id, int tag)
{
if (seg[id].val.mi >= tag)
return;
seg[id].val.sum += (tag - seg[id].val.mi) * seg[id].val.cnt;
seg[id].val.mi = tag;
seg[id].lazy_mx = tag;
}
void settag_add(int id, int tag)
{
seg[id].val.sum += seg[id].val.len * tag;
seg[id].val.mi += tag;
seg[id].val.sc += tag;
seg[id].lazy_add += tag;
if (seg[id].lazy_mx != -1)
seg[id].lazy_mx += tag;
}
void down(int id)
{
if (seg[id].lazy_add != 0)
{
settag_add(lson, seg[id].lazy_add);
settag_add(rson, seg[id].lazy_add);
}
if (seg[id].lazy_mx != -1)
{
settag_mx(lson, seg[id].lazy_mx);
settag_mx(rson, seg[id].lazy_mx);
}
seg[id].lazy_add = 0;
seg[id].lazy_mx = -1;
}
void modify_mx(int id, int l, int r, int ql, int qr, int x)
{
if (seg[id].val.mi >= x)
return;
if (ql <= l && r <= qr && x < seg[id].val.sc)
{
settag_mx(id, x);
return;
}
down(id);
int mid = l + r >> 1;
if (qr <= mid)
modify_mx(lson, l, mid, ql, qr, x);
else if (ql > mid)
modify_mx(rson, mid + 1, r, ql, qr, x);
else
{
modify_mx(lson, l, mid, ql, qr, x);
modify_mx(rson, mid + 1, r, ql, qr, x);
}
up(id);
}
void modify_add(int id, int l, int r, int ql, int qr, int x)
{
if (ql <= l && r <= qr)
{
settag_add(id, x);
return;
}
down(id);
int mid = l + r >> 1;
if (qr <= mid)
modify_add(lson, l, mid, ql, qr, x);
else if (ql > mid)
modify_add(rson, mid + 1, r, ql, qr, x);
else
{
modify_add(lson, l, mid, ql, qr, x);
modify_add(rson, mid + 1, r, ql, qr, x);
}
up(id);
}
info query(int id, int l, int r, int ql, int qr)
{
if (ql <= l && r <= qr)
{
return seg[id].val;
}
down(id);
int mid = l + r >> 1;
if (qr <= mid)
return query(lson, l, mid, ql, qr);
else if (ql > mid)
return query(rson, mid + 1, r, ql, qr);
else
return query(lson, l, mid, ql, qr) + query(rson, mid + 1, r, ql, qr);
}
void solve()
{
cin >> n >> q;
for (int i = 1; i <= n; ++i)
cin >> a[i];
build(1, 1, n);
while (q--)
{
int op, l, r, x;
cin >> op >> l >> r;
if (op == 1)
{
if (l <= r)
cout << query(1, 1, n, l, r).sum << endl;
else
cout << query(1, 1, n, l, n).sum + query(1, 1, n, 1, r).sum << endl;
}
else
{
cin >> x;
if (l <= r)
{
modify_add(1, 1, n, l, r, -x);
modify_mx(1, 1, n, l, r, 0);
}
else
{
modify_add(1, 1, n, l, n, -x);
modify_add(1, 1, n, 1, r, -x);
modify_mx(1, 1, n, l, n, 0);
modify_mx(1, 1, n, 1, r, 0);
}
}
}
}




